Слайд 2Устная работа
1. Как сложить две десятичные дроби?
2. Как сложить две обыкновенные дроби?
3.

Вычислить: 4 + 1,5 =
6,3 + 3,4 =
7,2 – 4,1 =
Слайд 3Устная работа
4. Как сравнить десятичные дроби?
5. Как сравнить обыкновенные дроби, если:
а)

знаменатели равны;
б) числители равны;
в) числитель и знаменатель – разные.
6. Сравнить: 1,3 и 2,4;
3,15 и 3,17;
и ;
и ;
и .
Слайд 4Устная работа
7. Какие числа называются отрицательными?
8. Какие числа называются положительными?
9. Какие числа

называются противоположными?
10. Назовите положительные, отрицательные и противоположные числа:
-5,2; 35; 7,8; 5,2; -19; 24; -1,7; 28,6; 19; ½; -16,7; 107; 293; -½; 25,6; 15,015; -¾; 27½; -5,2; ¼; -35.
Слайд 5Когда возникли отрицательные числа? Где? Какие действия с ними умели выполнять древние?
Отрицательные

числа появились приблизительно 2100 лет тому назад в Древнем Китае.
Древние толковали о «долге» (отрицательные числа) и «имуществе» (положительные числа). Долгое время такие числа считали «несуществующими» прежде всего из-за того, что принятое истолкование для положительных и отрицательных чисел «имущество – долг» приводило к недоумениям: можно сложить или вычесть «имущество» или «долги», но как понимать произведение «имущества» и «долга»? Однако несмотря на такие сомнения и недоумения действия сложения, вычитания, умножения и деления выполнялись. Правила вычисления были предложены греческим математиком Диофантом еще в
III в нашей эры.
Слайд 6Рассмотрим следующие задачи:
1. В книге доходов и расходов купца сделаны следующие записи:
Необходимо

выяснить прибыльное ли дело у купца или он имеет долг?
Решение: 1. 200 + 500 + 600 = 1300 (прибыль)
2. (-500) + (- 200) + (- 300) = -1000 (убыток)
3. 1300 + (- 1000) = 300 (прибыль)
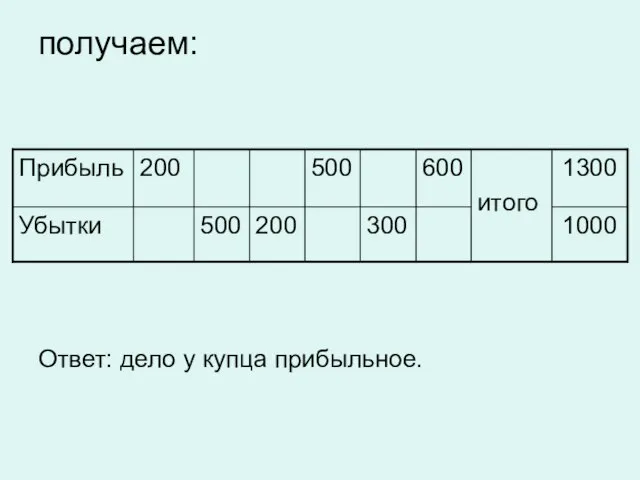
Слайд 7получаем:
Ответ: дело у купца прибыльное.
Слайд 82. Игра в кости
Надо узнать кто из участников игры выиграл, если:
- первый

игрок получил 5 штрафных и еще
7 штрафных очков;
- второй игрок получил 3 очка и 3 штрафных очков;
- третий игрок получил 4 штрафных очка и
5 очков;
- четвертый игрок получил 9 очков и
11 штрафных очков?
Слайд 9Решение:
1). -5 + (- 7) = - 12 (первый игрок)
2). 3 +

(- 3) = 0 (второй игрок)
3). (– 4) + 5 = 1 (третий игрок)
4). 9 + (- 11) = -2 (четвертый игрок)
Ответ: третий игрок выиграл.
Слайд 10Вычислить устно:
3 + (- 2) = - 5 + 4 =

- 4 + (-1) = 4,5 + (- 3) =
2 + (- 2) = 0 + (- 7) =
- 6,5 + 2 = - 8,2 + 0 =
- Какие можно сделать выводы?
Слайд 11Правила сложения чисел с разными знаками
- при сложении двух отрицательных

чисел складываем модули и перед полученным числом ставим знак «минус»;
- при сложении противоположных чисел получается нуль.
- при сложении двух чисел с разными знаками из большего модуля вычитаем меньший, и перед полученным числом, ставим знак того числа, модуль которого больше.










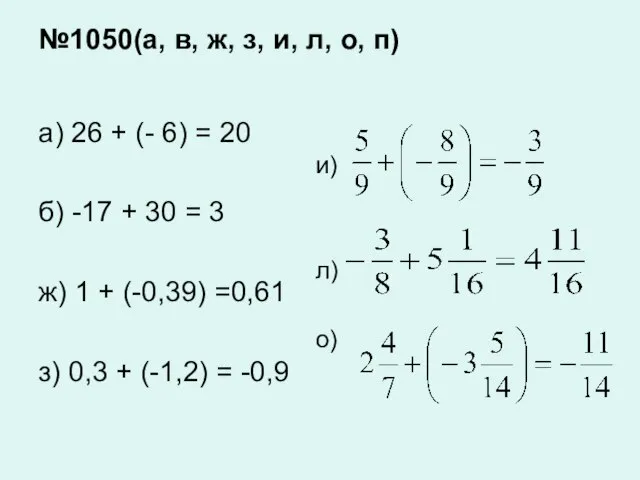


 ПРЕЗЕНТАЦИЯHINO 500
ПРЕЗЕНТАЦИЯHINO 500 Презентация на тему Зимние праздники в разных странах
Презентация на тему Зимние праздники в разных странах  RoomTour show. Экскурсия по домам медийных личностей
RoomTour show. Экскурсия по домам медийных личностей Работа со счетом До выяснения
Работа со счетом До выяснения Презентация на тему Просто и сложно
Презентация на тему Просто и сложно  ЧТО РАСТЕТ НА ПОДОКОННИКЕ
ЧТО РАСТЕТ НА ПОДОКОННИКЕ Возможности
Возможности Профилактика ОРВИ у детей, в период смены природно-климатических условий
Профилактика ОРВИ у детей, в период смены природно-климатических условий Влияние на психоэмоциональное состояние пользователей при ежедневном воздействии на них электромагнитных излучений
Влияние на психоэмоциональное состояние пользователей при ежедневном воздействии на них электромагнитных излучений Повторение сложения и вычитания в пределах 100 и таблицы умножения
Повторение сложения и вычитания в пределах 100 и таблицы умножения Quick Pay Service
Quick Pay Service Презентация на тему Разбор по членам предложения Как устроен наш язык
Презентация на тему Разбор по членам предложения Как устроен наш язык  портрет. поэтапное рисование
портрет. поэтапное рисование Герпесвирусные инфекции
Герпесвирусные инфекции Живопись
Живопись ПРЕМИАЛЬНЫЕ СТЕЙКИ И МЯСО ДЛЯ ШАШЛЫКА В МАРИНАДАХ
ПРЕМИАЛЬНЫЕ СТЕЙКИ И МЯСО ДЛЯ ШАШЛЫКА В МАРИНАДАХ ГСиУ_Л№1
ГСиУ_Л№1 Морфологический критерий вида
Морфологический критерий вида Школа здоровья для людей с ССЗ
Школа здоровья для людей с ССЗ Концепция преподавания философии студентам-заочникам
Концепция преподавания философии студентам-заочникам Формулы приветствия, прощания
Формулы приветствия, прощания Первобытный человек
Первобытный человек Chief executive officer wealth creation coaching
Chief executive officer wealth creation coaching Слитное и раздельное написание не с наречиями
Слитное и раздельное написание не с наречиями Психология для детей. Путешествие в страну настроений и эмоций
Психология для детей. Путешествие в страну настроений и эмоций Прямоугольный треугольник
Прямоугольный треугольник Цемент Холсим 500
Цемент Холсим 500 Великая депрессия
Великая депрессия