Презентация на тему Сфера и шар 11 класс

План презентации:
Определение сферы, шара.
Уравнение сферы.
Взаимное расположение сферы и плоскости.
Площадь сферы.
Итог урока.

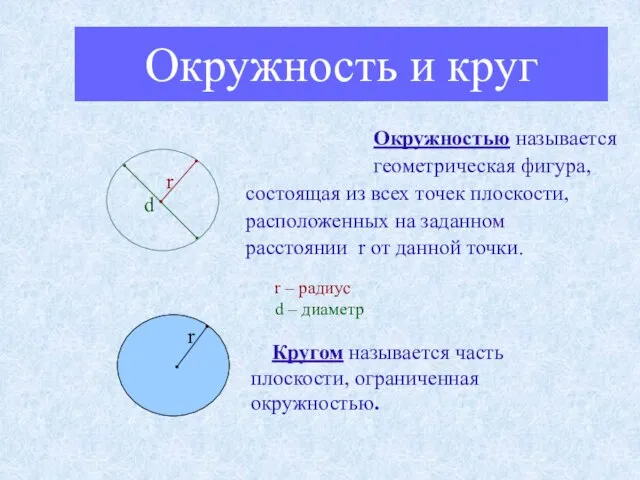
Окружность и круг
Окружностью называется
геометрическая фигура,
состоящая из всех точек плоскости,
расположенных на заданном
расстоянии r от данной точки.
r – радиус
d – диаметр
Кругом называется часть плоскости, ограниченная окружностью.

Определение сферы
Сферой называется поверхность, состоящая из всех точек
пространства, расположенных на данном расстоянии (R)
от данной точки (центра т.О).
D
О
R – радиус сферы – отрезок,
соединяющий любую точку
сферы с центром.
D – диаметр сферы – отрезок,
соединяющий любые 2 точки
сферы и проходящий через центр.
т. О – центр сферы

Шар
Шаром называется тело, ограниченное сферой.
Центр, радиус и диаметр сферы являются также центром, радиусом и диаметром шара.
Шар радиуса R и центром О содержит все точки пространства, которые расположены от т. О на расстоянии, не превышающем R.

Как изобразить сферу?
1. Отметить центр сферы (т.О)
2. Начертить окружность с
центром в т.О
3. Изобразить видимую
вертикальную дугу
4. Изобразить невидимую
вертикальную дугу
R
О
Изобразить видимую
горизонтальную дугу
6. Изобразить невидимую
горизонтальную дугу
7. Провести радиус сферы R

Уравнение окружности
О
С(х0;у0)
М(х;у)
Зададим прямоугольную систему координат Оxy
Построим окружность c центром в т. С и радиусом r
Расстояние от произвольной т.М(х;у) до т.С вычисляется по формуле:
МС = (x – x0)2 + (y – y0)2
МС = r , или МС2 = r2
Следовательно, уравнение
окружности имеет вид:
(x – x0)2 + (y – y0)2 = r2

Уравнение сферы
Зададим прямоугольную систему координат Оxyz
z
х
у
М(х;у;z)
R
C(x0;y0;z0)
Построим сферу c центром в т. С и радиусом R
МС = (x – x0)2 + (y – y0)2 + (z – z0)2
МС = R , или МС2 = R2
Следовательно, уравнение
сферы имеет вид:
(x – x0)2 + (y – y0)2 + (z – z0)2 = R2

Задача 1.
Зная координаты центра С(2;-3;0) и радиус сферы R=5, записать уравнение сферы.
Решение:
так как уравнение сферы с радиусом R и центром в точке С(х0;у0;z0) имеет вид
(х-х0)2 + (у-у0)2 + (z-z0)2=R2, а координаты центра данной сферы С(2;-3;0) и радиус R=5, то уравнение данной сферы
(x-2)2 + (y+3)2 + z2=25
Ответ: (x-2)2 + (y+3)2 + z2=25

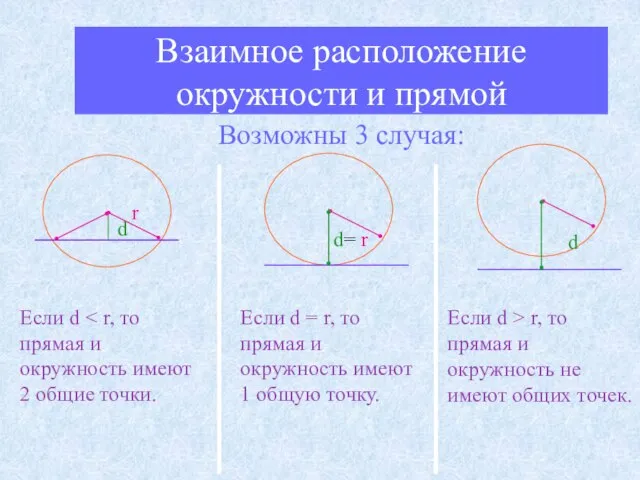
Взаимное расположение окружности и прямой
Возможны 3 случая:
d
d
r
Если d < r, то прямая и окружность имеют 2 общие точки.
d= r
Если d = r, то прямая и окружность имеют 1 общую точку.
Если d > r, то прямая и окружность не имеют общих точек.

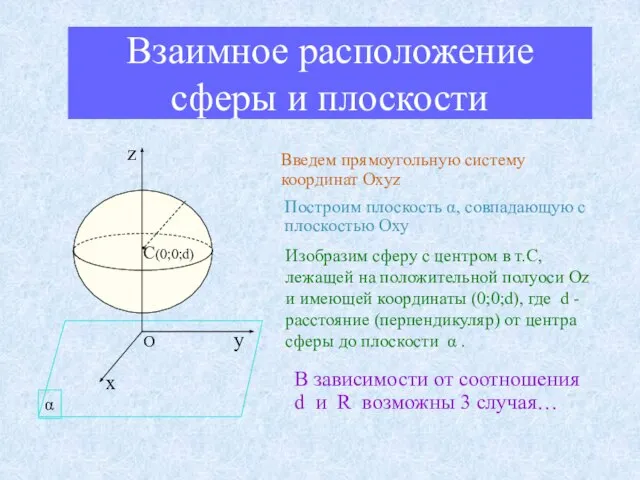
Взаимное расположение сферы и плоскости
Введем прямоугольную систему координат Oxyz
Построим плоскость α, совпадающую с плоскостью Оху
Изобразим сферу с центром в т.С, лежащей на положительной полуоси Oz и имеющей координаты (0;0;d), где d - расстояние (перпендикуляр) от центра сферы до плоскости α .
В зависимости от соотношения d и R возможны 3 случая…

Взаимное расположение сферы и плоскости
r
М
Рассмотрим 1 случай:
d < R, т.е. если расстояние от центра сферы до плоскости меньше радиуса сферы, то сечение сферы плоскостью есть окружность радиусом r.
r = R2 - d2
Сечение шара плоскостью есть круг.

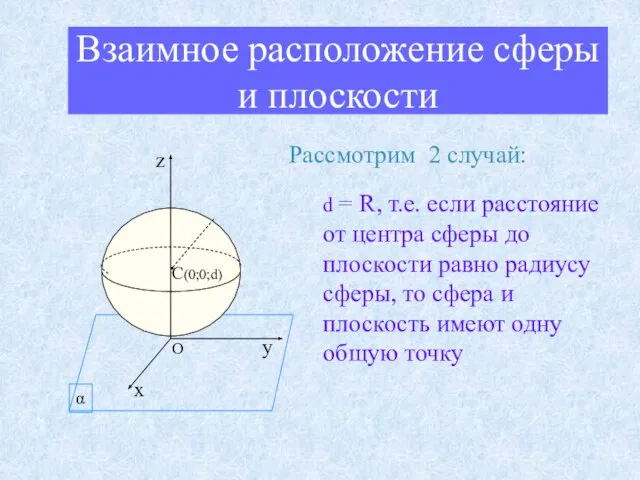
Взаимное расположение сферы и плоскости
Рассмотрим 2 случай:
d = R, т.е. если расстояние от центра сферы до плоскости равно радиусу сферы, то сфера и плоскость имеют одну общую точку

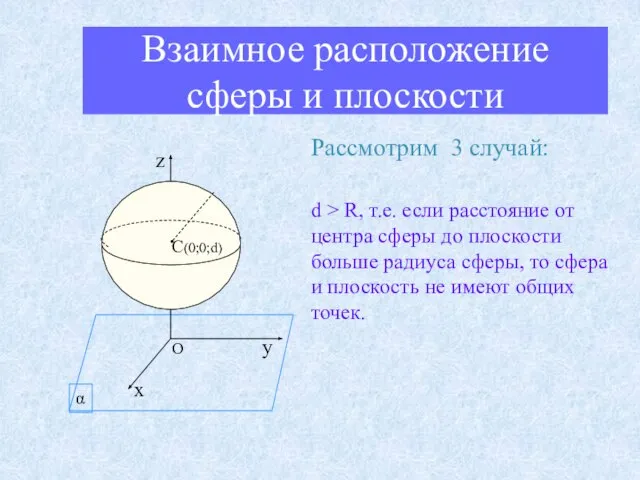
Взаимное расположение сферы и плоскости
Рассмотрим 3 случай:
d > R, т.е. если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.

Задача 2.
Шар радиусом 41 дм пересечен плоскостью, находящейся на расстоянии 9 дм от центра. Найти радиус сечения.
Дано:
Шар с центром в т.О
R=41 дм
α - секущая плоскость
d = 9 дм
Найти: rсеч = ?
Решение:
Рассмотрим ∆ОМК – прямоугольный
ОМ = 41 дм; ОК = 9 дм; МК = r, r = R2 - d2
по теореме Пифагора: МК2 = r2 = 412- 92 = 1681 - 81=1600, отсюда rсеч = 40 дм
Ответ: rсеч = 40 дм

Площадь сферы и шара
Сферу нельзя развернуть на плоскость.
Опишем около сферы многогранник, так чтобы сфера касалась всех его граней.
За площадь сферы принимается предел последовательности площадей поверхностей описанных около сферы многогранников при стремлении к нулю наибольшего размера каждой грани
Площадь сферы радиуса R: Sсф=4πR2
Sшара=4 Sкруга
т.е.: площадь поверхности шара равна учетверенной площади большего круга

Задача 3.
Найти площадь поверхности сферы,
радиус которой равен 6 см.
Дано:
сфера
R = 6 см
Найти:
Sсф = ?
Решение:
Sсф = 4πR2
Sсф = 4π 62 = 144π см2
Ответ: Sсф = 144π см2