Содержание
- 2. 10.8. Типы диэлектриков. Поляризация диэлектриков. В зависимости от вида молекул диэлектрики делятся на три группы. Первую
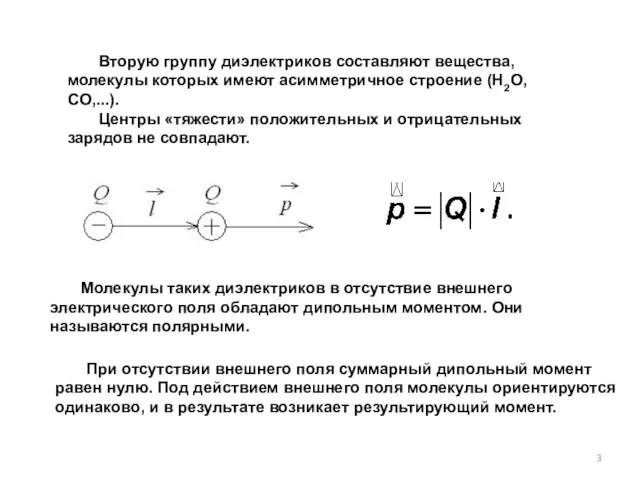
- 3. Вторую группу диэлектриков составляют вещества, молекулы которых имеют асимметричное строение (H2O, CO,...). Центры «тяжести» положительных и
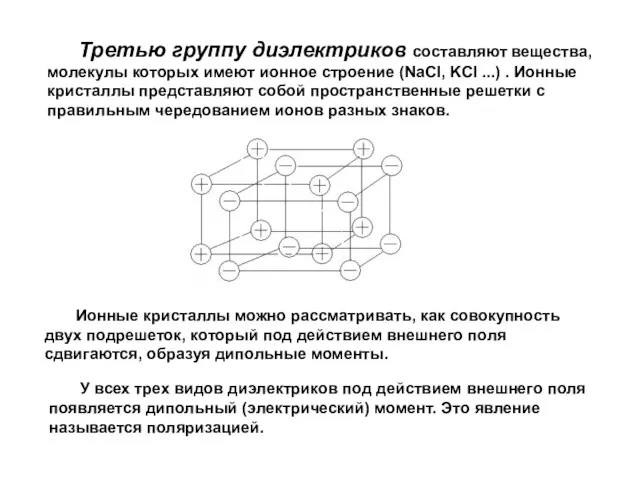
- 4. Ионные кристаллы можно рассматривать, как совокупность двух подрешеток, который под действием внешнего поля сдвигаются, образуя дипольные
- 5. Поляризацией диэлектрика называется процесс ориентации диполей или появления под воздействием внешнего электрического поля ориентированных по полю
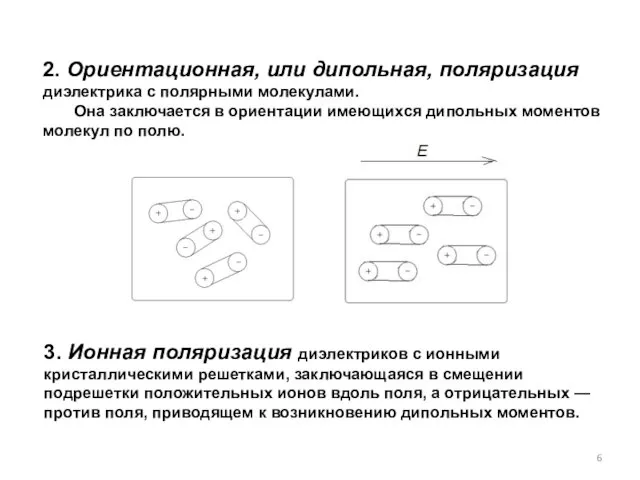
- 6. 2. Ориентационная, или дипольная, поляризация диэлектрика с полярными молекулами. Она заключается в ориентации имеющихся дипольных моментов
- 7. Поляризованность и напряженность поля в диэлектрике При помещении диэлектрика во внешнее электрическое поле он поляризуется, т.
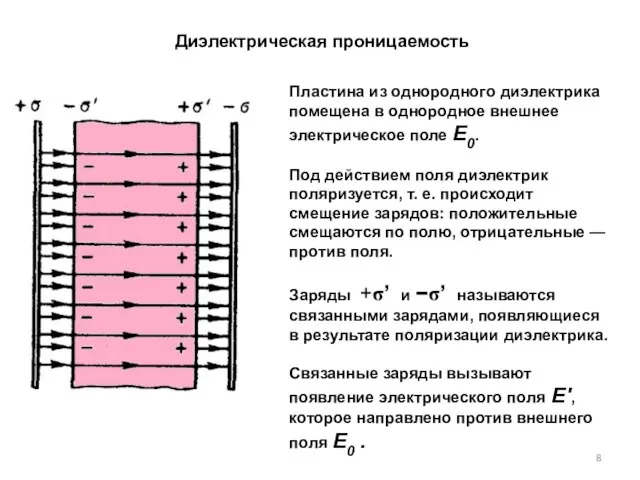
- 8. Пластина из однородного диэлектрика помещена в однородное внешнее электрическое поле Е0. Под действием поля диэлектрик поляризуется,
- 9. - поле, созданное двумя бесконечными заряженными плоскостями. Определим поверхностную плотность связанных зарядов σ'. Полный дипольный момент
- 10. откуда напряженность результирующего поля внутри диэлектрика равна: Безразмерная величина называется диэлектрической проницаемостью среды. ε показывает, во
- 11. 10.9. Электрическое смещение. Теореме Гаусса для электростатического поля в диэлектрике Вектор напряженности Е, переходя через границу
- 12. Для произвольной замкнутой поверхности S поток вектора D сквозь эту поверхность определяется выражением: Dn — проекция
- 13. тогда поток вектора напряженности Е сквозь произвольную замкнутую поверхность равен: Для вакуума: - теорема Гаусса для
- 14. 10.10. Сегнетоэлектрики и пьезоэлектрики Сегнетоэлектрики — диэлектрики, обладающие в определенном интервале температур спонтанной (самопроизвольной) поляризованностью. При
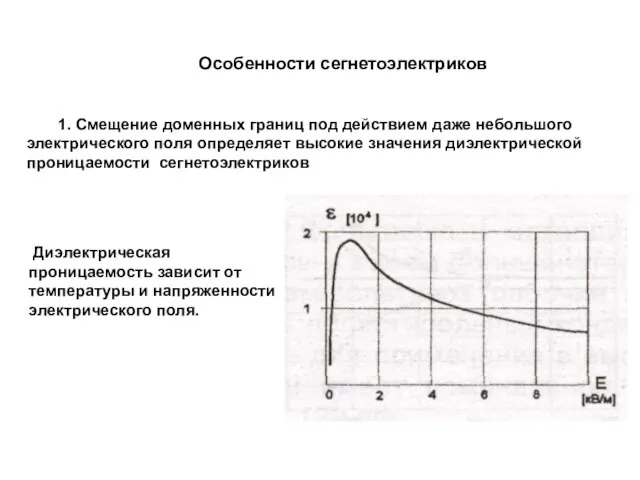
- 15. 1. Смещение доменных границ под действием даже небольшого электрического поля определяет высокие значения диэлектрической проницаемости сегнетоэлектриков
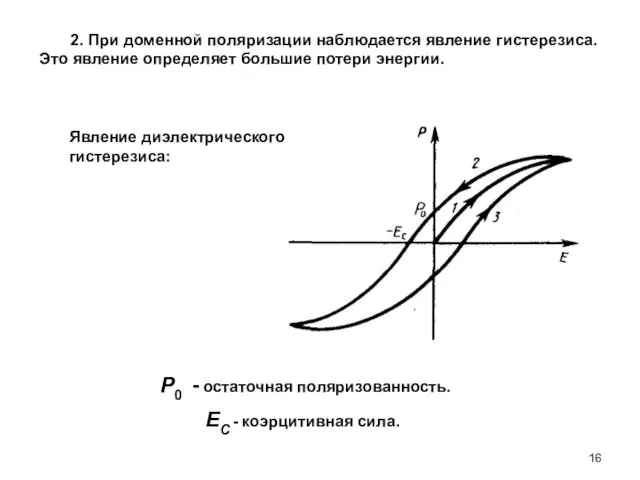
- 16. 2. При доменной поляризации наблюдается явление гистерезиса. Это явление определяет большие потери энергии. Явление диэлектрического гистерезиса:
- 17. 3. Сегнетоэлектрические свойства сильно зависят от температуры. Для каждого сегнетоэлектрика имеется определенная температура, выше которой его
- 18. Пьезоэлектрики К пьезоэлектрическим материалам относятся кристаллические и поликристаллические вещества с ярко выраженным пьезоэффектом. Пьезоэффект заключается в
- 19. Гексагональная элементарная ячейка содержит чередующиеся положительные и отрицательные ионы. При отсутствии внешних механических напряжений дипольный момент
- 20. 10.11. Электрическая емкость уединенного проводника. Конденсаторы. Рассмотрим уединенный проводник, т. е. проводник, который удален от других
- 21. Единица электроемкости — фарад (Ф): 1 Ф — емкость такого уединенного проводника, потенциал которого изменяется на
- 22. Конденсаторы Конденсаторы – это устройства, обладающие способностью при малых размерах и небольших относительно окружающих тел потенциалах
- 23. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов
- 24. 2. Определим емкость цилиндрического конденсатора, состоящего из двух полых коаксиальных цилиндров с радиусами r1 и r2
- 25. 3. Определим емкость сферического конденсатора, состоящего из двух концентрических обкладок, разделенных сферическим слоем диэлектрика. Разность потенциалов
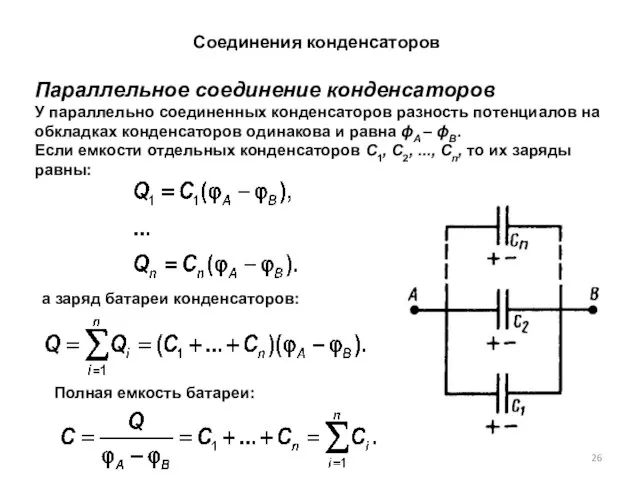
- 26. Соединения конденсаторов Параллельное соединение конденсаторов У параллельно соединенных конденсаторов разность потенциалов на обкладках конденсаторов одинакова и
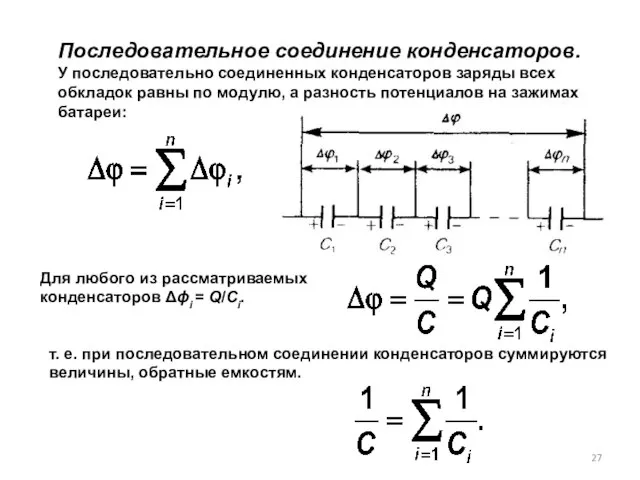
- 27. Последовательное соединение конденсаторов. У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов
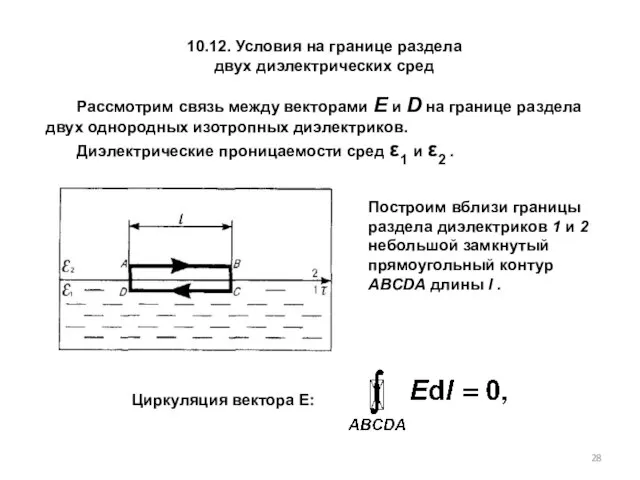
- 28. 10.12. Условия на границе раздела двух диэлектрических сред Рассмотрим связь между векторами Е и D на
- 29. Значит: Заменив, согласно проекции вектора Е проекциями вектора D, деленными на ε0ε, получим: Тогда:
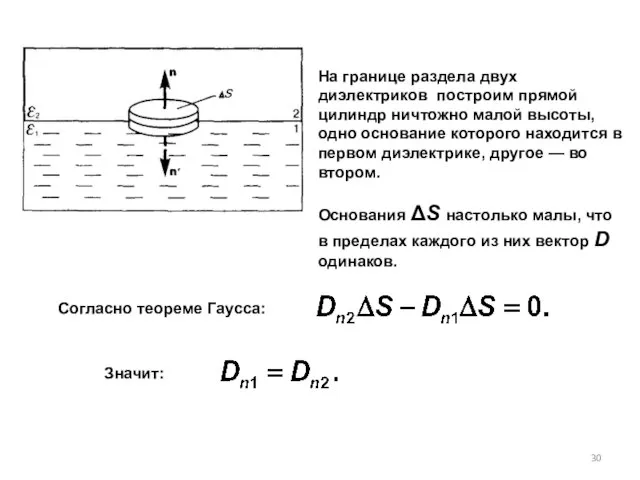
- 30. На границе раздела двух диэлектриков построим прямой цилиндр ничтожно малой высоты, одно основание которого находится в
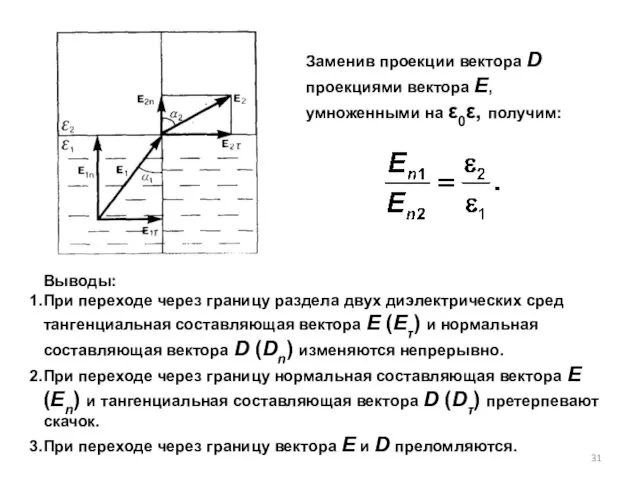
- 31. Заменив проекции вектора D проекциями вектора Е, умноженными на ε0ε, получим: Выводы: При переходе через границу
- 32. Закон преломления линий напряженности Е и линий смещения D : Эта формула показывает, что, входя в
- 33. 10.13. Проводники в электростатическом поле Если проводник поместить в электростатическое поле, то это поле будет действовать
- 34. Заряд Q, находящийся внутри проводника в некотором объеме, ограниченном произвольной замкнутой поверхностью, равен: так как во
- 35. Если во внешнее электростатическое поле внести нейтральный проводник, то свободные заряды будут перемещаться: положительные — по
- 37. Скачать презентацию























 Презентация на тему Олимпийские игры в Москве 1980
Презентация на тему Олимпийские игры в Москве 1980  Национализм как политическая идеология
Национализм как политическая идеология Презентация на тему Решение задач на нахождение площади поверхности и объемов тел вращения
Презентация на тему Решение задач на нахождение площади поверхности и объемов тел вращения  Moderní cukrovar HROCHŮV TÝNEC
Moderní cukrovar HROCHŮV TÝNEC Система работы учителя математики с родителями при подготовке учащихся к государственной итоговой аттестации в форме ЕГЭ
Система работы учителя математики с родителями при подготовке учащихся к государственной итоговой аттестации в форме ЕГЭ Внешняя политика Александра I в 1801-1812 гг.
Внешняя политика Александра I в 1801-1812 гг. Основные ошибки при подаче документов на лицензирование
Основные ошибки при подаче документов на лицензирование Презентация на тему Изобразительное искусство классицизма и рококо
Презентация на тему Изобразительное искусство классицизма и рококо КИНЕШМА
КИНЕШМА Обработка нижнего среза изделия
Обработка нижнего среза изделия Педагогическая практика организации внеурочной и внеклассной деятельности
Педагогическая практика организации внеурочной и внеклассной деятельности Положение об общественном совете муниципального образования Северодвинск
Положение об общественном совете муниципального образования Северодвинск Луи , ПАСТЕР (Pasteur)
Луи , ПАСТЕР (Pasteur) Хохломская роспись
Хохломская роспись Горячая линия
Горячая линия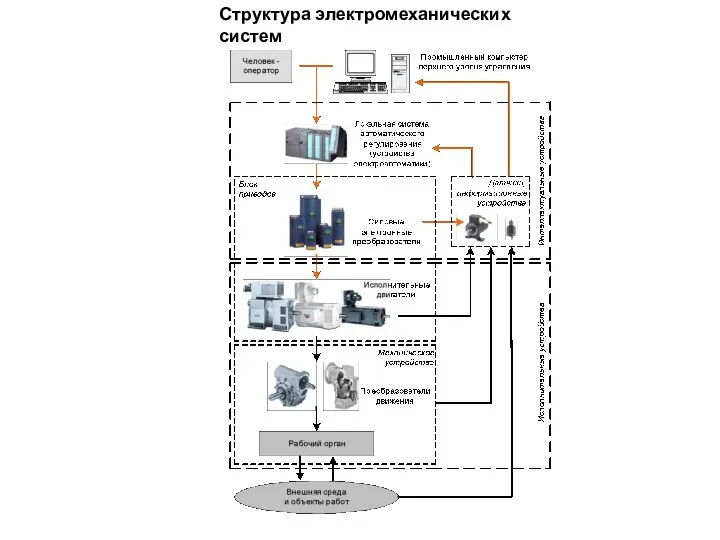 Структура электромеханических систем
Структура электромеханических систем Характер человека
Характер человека Преодоление сложностей при запоминании таблицы умножения
Преодоление сложностей при запоминании таблицы умножения Презентация на тему Юридическая клиника в кыргызско-российском славянском университете имени Бориса Ельцина
Презентация на тему Юридическая клиника в кыргызско-российском славянском университете имени Бориса Ельцина  Презентация на тему Военно-патриотическое воспитание
Презентация на тему Военно-патриотическое воспитание Обобщающий урок во 2 классе
Обобщающий урок во 2 классе Дистрибуция прессы в сети супермаркетов в России. Тенденции и перспективы развития.
Дистрибуция прессы в сети супермаркетов в России. Тенденции и перспективы развития. Использование 3D технологии в медицине
Использование 3D технологии в медицине Кружок робототехники
Кружок робототехники Война за независимость США
Война за независимость США Современная теория фотосинтеза
Современная теория фотосинтеза Программный комплекс «Карат» предназначен для создания в базе данных показателей любого типа, ручного ввода или автоматической п
Программный комплекс «Карат» предназначен для создания в базе данных показателей любого типа, ручного ввода или автоматической п Prezentacia_лекція_10-1_ТЕК (3)
Prezentacia_лекція_10-1_ТЕК (3)