Презентация на тему Двугранный угол 10 класс

Основные задачи урока:
Ввести понятие двугранного угла и его линейного угла
Рассмотреть задачи на применение этих понятий

Определение:
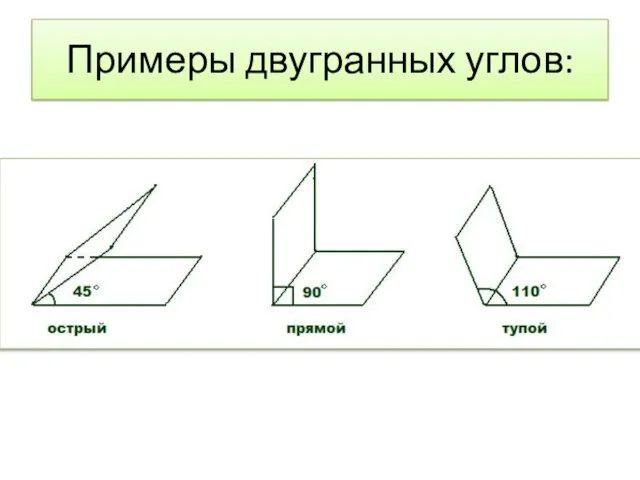
Двугранным углом называется фигура, образованная двумя полуплоскостями с общей граничной прямой.

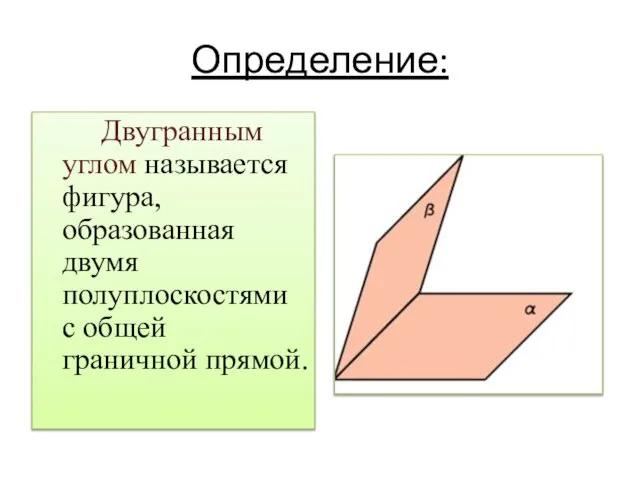
Величиной двугранного угла называется величина его линейного угла.
AF ⊥ CD
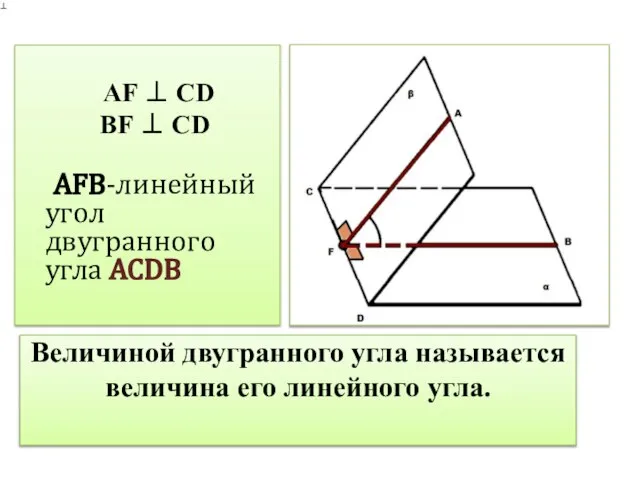
BF ⊥ CD
AFB-линейный угол двугранного угла ACDВ

Докажем, что все линейные углы двугранного угла равны друг другу.
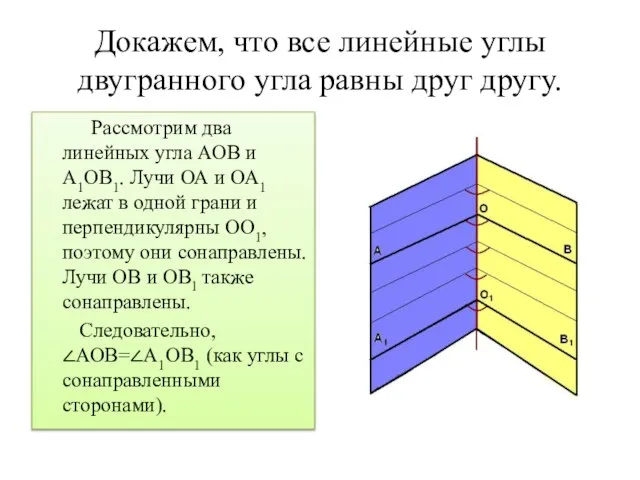
Рассмотрим два линейных угла АОВ и А1ОВ1. Лучи ОА и ОА1 лежат в одной грани и перпендикулярны ОО1, поэтому они сонаправлены. Лучи ОВ и ОВ1 также сонаправлены.
Следовательно, ∠АОВ=∠А1ОВ1 (как углы с сонаправленными сторонами).

Примеры двугранных углов:

Определение:
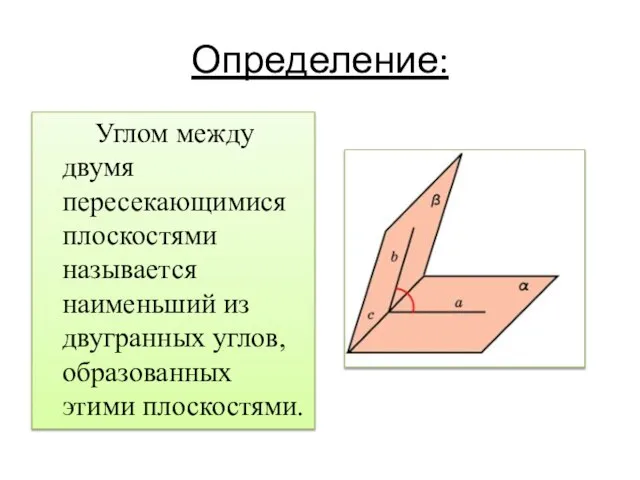
Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованных этими плоскостями.

Задача 1:
В кубе A…D1 найдите угол между плоскостями ABC и CDD1.
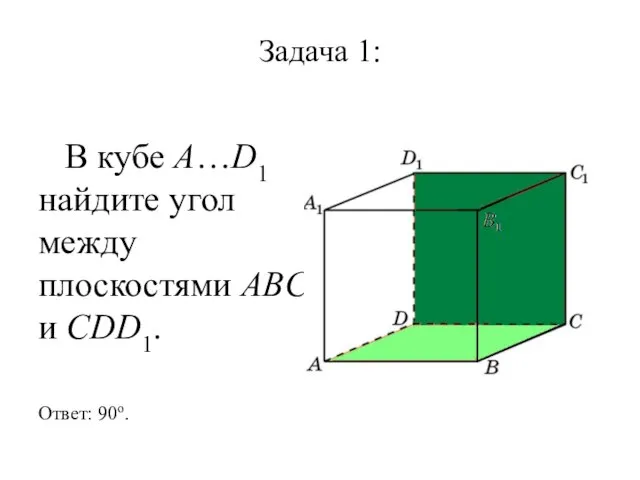
Ответ: 90o.

Задача 2:
В кубе A…D1 найдите угол между плоскостями ABC и CDA1.
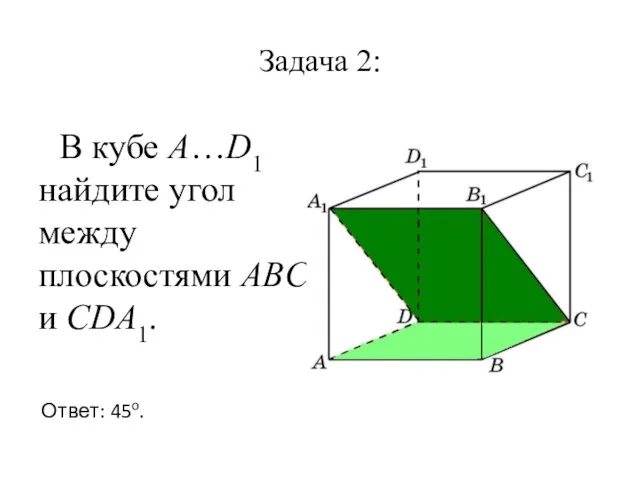
Ответ: 45o.

Задача 3:
В кубе A…D1 найдите угол между плоскостями ABC и BDD1.
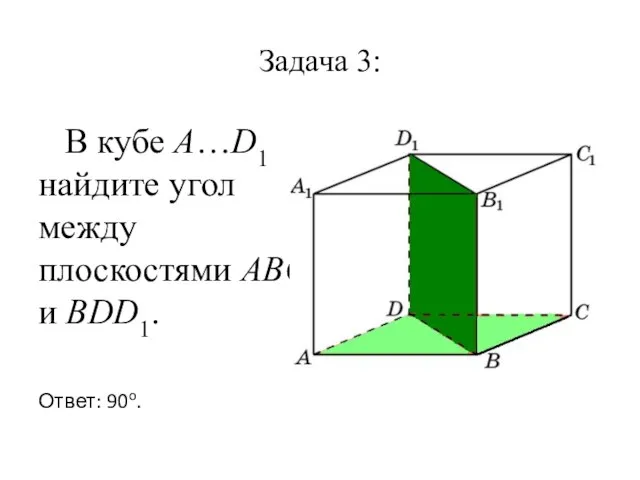
Ответ: 90o.

Задача 4:
В кубе A…D1 найдите угол между плоскостями ACC1 и BDD1.
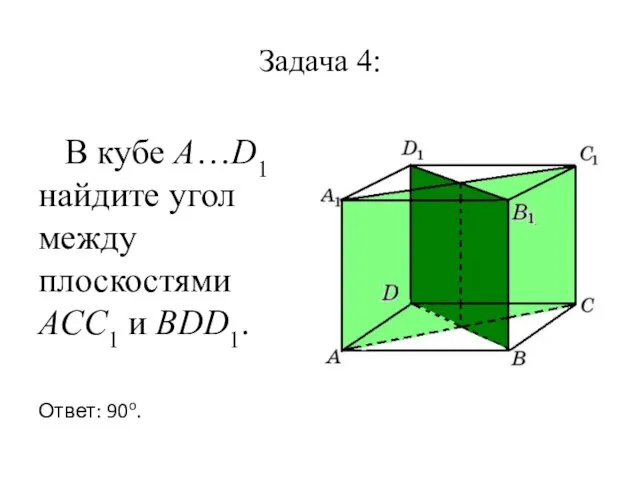
Ответ: 90o.

Задача 5:
В кубе A…D1 найдите угол между плоскостями
BC1D и BA1D.
Решение:
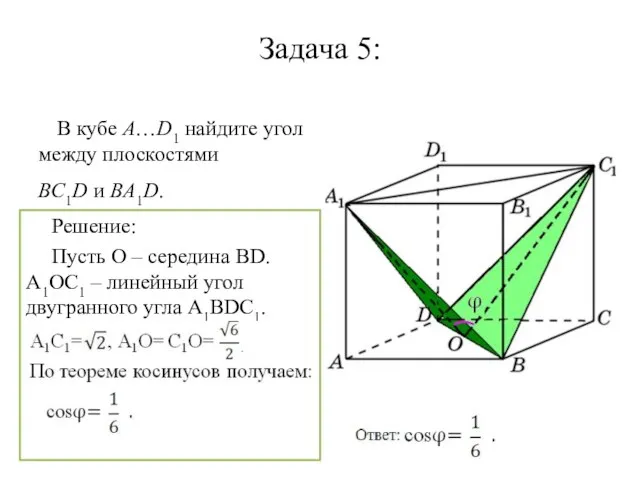
Пусть О – середина ВD. A1OC1 – линейный угол двугранного угла А1ВDС1.

Задача 6:
В тетраэдре DABC все ребра равны, точка М – середина ребра АС. Докажите, что ∠DMB – линейный угол двугранного угла BACD.

Решение:
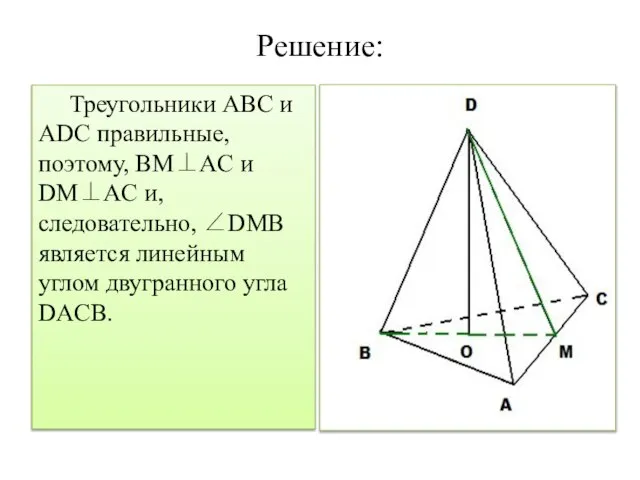
Треугольники ABC и ADC правильные, поэтому, BM⊥AC и DM⊥AC и, следовательно, ∠DMB является линейным углом двугранного угла DACB.

Задача 7:
Из вершины В треугольника АВС, сторона АС которого лежит в плоскости α, проведен к этой плоскости перпендикуляр ВВ1. Найдите расстояние от точки В до прямой АС и до плоскости α, если АВ=2, ∠ВАС=1500 и двугранный угол ВАСВ1 равен 450.

Решение:
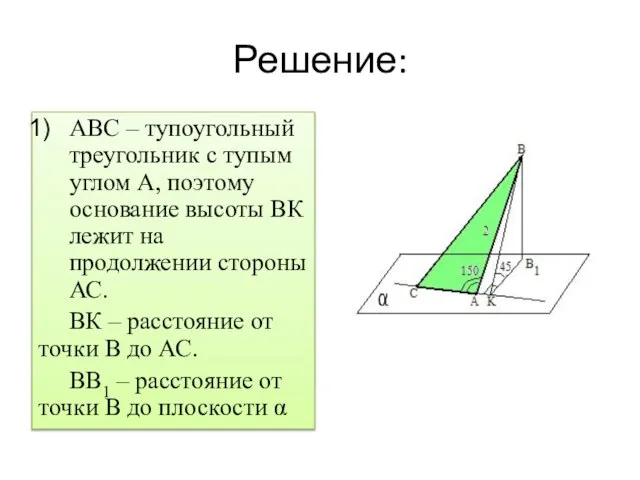
АВС – тупоугольный треугольник с тупым углом А, поэтому основание высоты ВК лежит на продолжении стороны АС.
ВК – расстояние от точки В до АС.
ВВ1 – расстояние от точки В до плоскости α

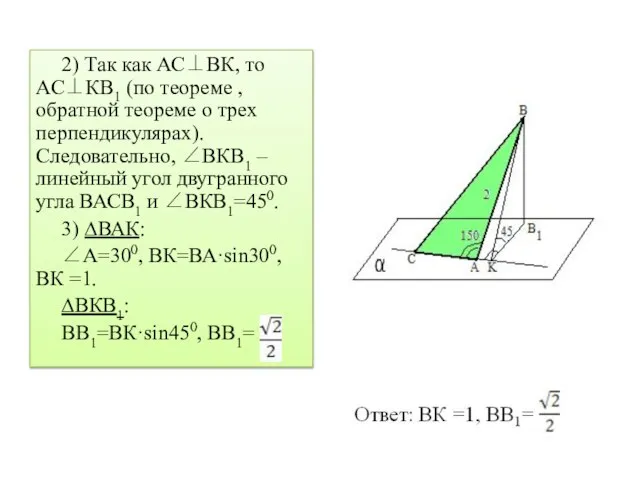
2) Так как АС⊥ВК, то АС⊥КВ1 (по теореме , обратной теореме о трех перпендикулярах). Следовательно, ∠ВКВ1 – линейный угол двугранного угла ВАСВ1 и ∠ВКВ1=450.
3) ∆ВАК:
∠А=300, ВК=ВА·sin300, ВК =1.
∆ВКВ1:
ВВ1=ВК·sin450, ВВ1=