Содержание
- 2. Вопрос1 Виды модуляции, используемые для передачи цифровых сигналов. В предыдущей лекции говорилось, что для качественной передачи
- 3. Вопрос1 Виды модуляции, используемые для передачи цифровых сигналов Рисунок 1 Процесс преобразования сигналов, импульсно-кодовая модуляция Если
- 4. Идея состоит в использовании метода кодирования с предсказанием или дифференциальной импульсно-кодовой модуляции (ДИКМ). В этом случае
- 5. Вопрос1 Виды модуляции, используемые для передачи цифровых сигналов В вычитающем устройстве определяется разность действительного х (п)
- 6. Вопрос1 Виды модуляции, используемые для передачи цифровых сигналов Слайд 6 P'(п) = где ak - коэффициенты,
- 7. Вопрос 2 Ортогональные преобразования. Слайд 7 Одними из наиболее распространенных средств обработки как одномерных, так и
- 8. Вопрос 2 Ортогональные преобразования Действительные коэффициенты ряда Фурье аk, bk определяются соотношениями a0 =(2/T)* ak =
- 9. Вопрос 2 Ортогональные преобразования Можно показать, что произвольный конечный набор сигналов {Si(t)}(i=1,2,…,M), где каждый элемент множества
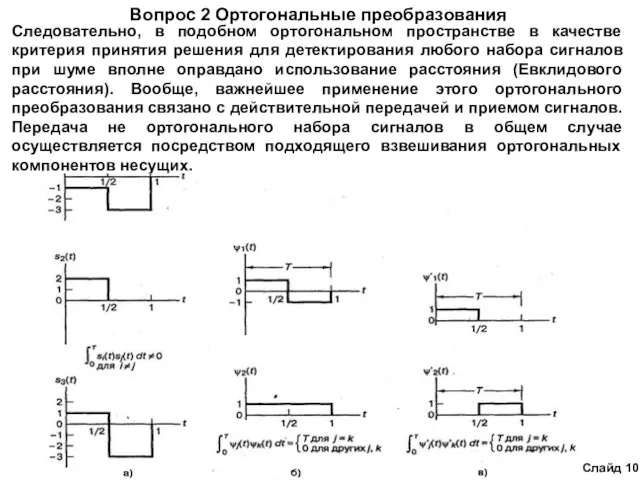
- 10. Вопрос 2 Ортогональные преобразования Слайд 10 Следовательно, в подобном ортогональном пространстве в качестве критерия принятия решения
- 11. ВОПРОС 2 Ортогональные преобразования Слайд 11 В векторном пространстве это аналогично представлению данного вектора в различных
- 12. ВОПРОС 3 Аналого-цифровые и цифро-аналоговые преобразователи Устройства, в целом выполняющие преобразования аналоговых сигналов в цифровые и
- 13. ВОПРОС 3 Аналого-цифровые и цифро-аналоговые преобразователи Возможно построение АЦП на основе ЦАП. Схема такого АЦП показана
- 15. Скачать презентацию
Слайд 2Вопрос1 Виды модуляции, используемые для передачи цифровых сигналов.
В предыдущей лекции говорилось, что
Вопрос1 Виды модуляции, используемые для передачи цифровых сигналов.
В предыдущей лекции говорилось, что

аналоговых сигналов при равномерном и неравномерном квантовании нужно иметь соответственно 4096 или 256 уровней квантования, т.е. необходимо использовать 12- или 8- разрядный код. Различают линейное и нелинейное кодирование.
Линейным кодированием называется кодирование равномерно квантованного сигнала, а нелинейным - неравномерно квантованного сигнала.
Код, формируемый в кодере, называется параллельным, если импульсные сигналы (1 и 0), входящие в состав m-разрядной кодовой группы, появляются на разных выходах кодера одновременно, причем каждому выходу кодера соответствует сигнал определенного разряда. Код называется последовательным, если все сигналы, входящие в состав m-разрядной кодовой группы, появляются на одном выходе кодера поочередно со сдвигом по времени (обычно начиная со старшего по весу разряда). Параллельный код может преобразовываться в последовательный, и наоборот.
Процесс преобразования сигналов АИМ путем кодирования каждой квантованной выборки цифровым кодом (Рис. 1) называется импульсно-кодовой модуляцией (ИКМ) или согласно английской аббревиатуре (PSM) .
Рис. 1 а) выделение мгновенных значений сигнала, б) дискретизация, в) квантование
Слайд 2
Слайд 3Вопрос1 Виды модуляции, используемые для передачи цифровых сигналов
Рисунок 1 Процесс преобразования сигналов,
Вопрос1 Виды модуляции, используемые для передачи цифровых сигналов
Рисунок 1 Процесс преобразования сигналов,
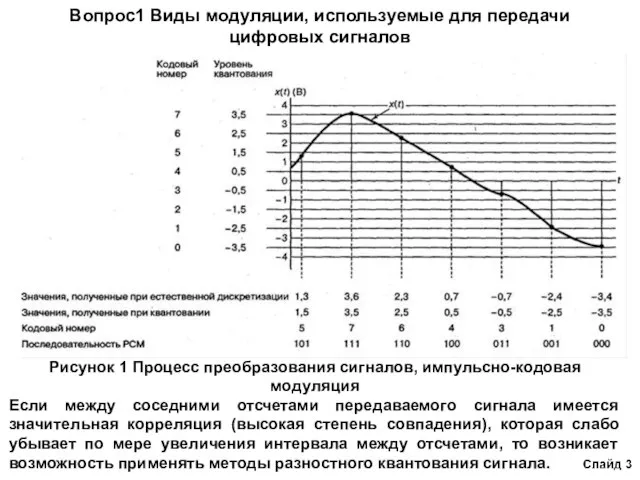
Если между соседними отсчетами передаваемого сигнала имеется значительная корреляция (высокая степень совпадения), которая слабо убывает по мере увеличения интервала между отсчетами, то возникает возможность применять методы разностного квантования сигнала.
Слайд 4Идея состоит в использовании метода кодирования с предсказанием или дифференциальной импульсно-кодовой модуляции
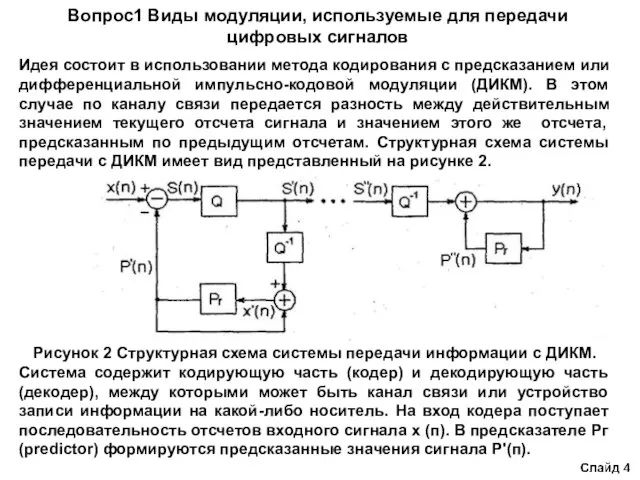
Рисунок 2 Структурная схема системы передачи информации с ДИКМ.
Система содержит кодирующую часть (кодер) и декодирующую часть (декодер), между которыми может быть канал связи или устройство записи информации на какой-либо носитель. На вход кодера поступает последовательность отсчетов входного сигнала х (п). В предсказателе Рг (predictor) формируются предсказанные значения сигнала P'(п).
Вопрос1 Виды модуляции, используемые для передачи цифровых сигналов
Слайд 5Вопрос1 Виды модуляции, используемые для передачи цифровых сигналов
В вычитающем устройстве определяется разность
Вопрос1 Виды модуляции, используемые для передачи цифровых сигналов
В вычитающем устройстве определяется разность

На вход декодера поступает сигнал S"(n), прошедший канал связи. В деквантователе Q-1 восстанавливается исходное число двоичных разрядов. В сумматоре происходит формирование выходного сигнала у (п) в соответствии с соотношением у(п) =P"(п) + S"(n), где P"(п) - предсказанное по предыдущим значениям выходного сигнала его текущее значение.
Рассмотрим формирование в кодере предсказанных значениям сигнала P'(п). Важно отметить, что предсказатели в кодере и декодере работают по идентичным алгоритмам. Квантованный сигнал ошибки предсказания S'(n) поступает во входящий в состав кодера деквантователь Q-1, в котором восстанавливается исходное число двоичных разрядов. Выходной сигнал деквантователя в сумматоре складывается с предсказанным значением P'(п), в результате чего формируется сигнал х’ (п), получающийся в результате выполнения таких же операций, что и выходной сигнал декодера у (п).
В общем случае предсказанные значения P'(п) вычисляются по формуле
Слайд 6Вопрос1 Виды модуляции, используемые для передачи цифровых сигналов
Слайд 6
P'(п) =
где ak -
Вопрос1 Виды модуляции, используемые для передачи цифровых сигналов
Слайд 6
P'(п) =
где ak -

Коэффициенты линейного предсказания находятся при помощи решения системы линейных уравнений (число которых равно порядку предсказания), а в качестве известных членов уравнения фигурируют значения корреляции между отсчетами.
Развитием метода ДИКМ является адаптивная импульсно-кодовая модуляция АДИКМ (Adaptive Differential Pulse Code Modulation - ADPCM). В соответствии с этим методом параметры квантователя Q и предсказателей Рг изменяются в зависимости от параметров передаваемого сигнала. Например, если средняя за определенный интервал времени скорость изменения входного сигнала х(п) увеличилась, шаг квантования также увеличивается, чтобы не возникало перегрузок в квантователе. Наоборот, если средняя скорость изменения входного сигнала уменьшилась, шаг квантования также уменьшается, чтобы уменьшить влияние шума квантования на передаваемую информацию.
Слайд 7
Вопрос 2 Ортогональные преобразования.
Слайд 7
Одними из наиболее распространенных средств обработки как одномерных,
Вопрос 2 Ортогональные преобразования.
Слайд 7
Одними из наиболее распространенных средств обработки как одномерных,

Напомним, что функции x(t) и y(t) называются ортогональными на отрезке (t1,t2), если их скалярное произведение равно нулю.
Это определение может быть распространено на дискретные сигналы, представляемые последовательностями чисел. Дискретные сигналы x(n) и у(n), имеющие по N отсчетов, называются ортогональными, если выполняется условие
Одним из наиболее известных примеров применения ортогонального преобразования является разложение периодического сигнала x(t) в ряд Фурье
x(t)=(1/2)a0 +
Слайд 8Вопрос 2 Ортогональные преобразования
Действительные коэффициенты ряда Фурье аk, bk определяются соотношениями
a0
Вопрос 2 Ортогональные преобразования
Действительные коэффициенты ряда Фурье аk, bk определяются соотношениями
a0

ak = (2/T)*
bk = (2/T)*
где ω0 = 2π/T, T - период повторения сигнала x(t).
Основное условие ортогональности можно сформулировать следующим образом: каждая функция набора базисных функций должна быть независимой от остальных функций набора. Каждая функция не должна интерферировать с другими функциями в процессе детектирования. С геометрической точки зрения все функции взаимно перпендикулярны. Пример подобного пространства с N = 3 показан на рисунке 3, где взаимно перпендикулярные оси обозначены . Одной из причин нашего внимания к ортогональному сигнальному пространству является то, что в нем проще всего определяется Евклидова мера расстояния, используемая в процессе детектирования. Стоит отметить, что даже если переданные сигналы формируют подобные пространства, они могут преобразовываться в линейную комбинацию ортогональных сигналов.
Слайд 9
Вопрос 2 Ортогональные преобразования
Можно показать, что произвольный конечный набор сигналов {Si(t)}(i=1,2,…,M), где
Вопрос 2 Ортогональные преобразования
Можно показать, что произвольный конечный набор сигналов {Si(t)}(i=1,2,…,M), где
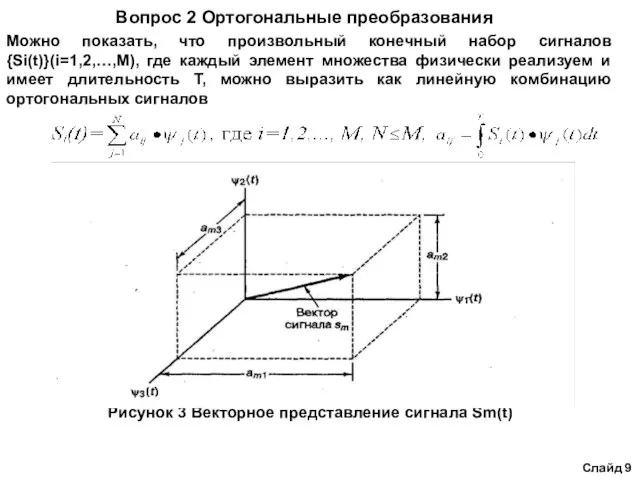
Рисунок 3 Векторное представление сигнала Sm(t)
Слайд 9
Слайд 10Вопрос 2 Ортогональные преобразования
Слайд 10
Следовательно, в подобном ортогональном пространстве в качестве критерия
Вопрос 2 Ортогональные преобразования
Слайд 10
Следовательно, в подобном ортогональном пространстве в качестве критерия
Слайд 11ВОПРОС 2 Ортогональные преобразования
Слайд 11
В векторном пространстве это аналогично представлению данного вектора
ВОПРОС 2 Ортогональные преобразования
Слайд 11
В векторном пространстве это аналогично представлению данного вектора

Норма вектора, в Rn мерном вещественном пространстве
Евклидова метрика для дискретных сигналов
Евклидова метрика для непрерывных величин
Слайд 12ВОПРОС 3 Аналого-цифровые и цифро-аналоговые преобразователи
Устройства, в целом выполняющие преобразования аналоговых сигналов
ВОПРОС 3 Аналого-цифровые и цифро-аналоговые преобразователи
Устройства, в целом выполняющие преобразования аналоговых сигналов

Рассмотрим принцип работы ЦАП (рисунок 5). Цифровой сигнал в двоичном коде (последовательном или параллельном) подается на буферный регистр RG. К выходам регистра RG подключены управляющие входы электронных ключей. К каждому из ключей подключены резисторы с сопротивлениями, соответствующими числу шагов квантования каждого из разрядов кодового слова цифрового сигнала. В зависимости от кодовой комбинации, т.е. включения и выключения соответствующих ключей, на входе ФНЧ будет присутствовать соответствующее напряжение. Смена кодовых комбинаций приведет к образованию на входе ФНЧ ступенчатого сигнала (рисунок 6). ФНЧ выделяет исходный аналоговый сигнал.
РР Рисунки 5 и 6
Слайд 12
Слайд 13
ВОПРОС 3 Аналого-цифровые и цифро-аналоговые преобразователи
Возможно построение АЦП на основе ЦАП. Схема
ВОПРОС 3 Аналого-цифровые и цифро-аналоговые преобразователи
Возможно построение АЦП на основе ЦАП. Схема
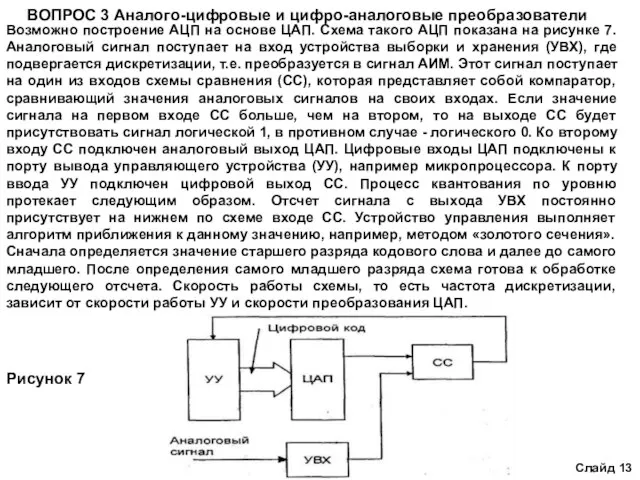
Рисунок 7
Слайд 13
 Отмена ЕНВД
Отмена ЕНВД Рынок земли(природных ресурсов)
Рынок земли(природных ресурсов) «Электричество и растения».
«Электричество и растения». Роль женщины-матери в духовно-нравственном воспитании детей
Роль женщины-матери в духовно-нравственном воспитании детей Риск-менеджмент. Теоретические основы рискологии. Лекция №1
Риск-менеджмент. Теоретические основы рискологии. Лекция №1 Моя любимая игра: ,,Страйкбол”
Моя любимая игра: ,,Страйкбол” Что такое Recognition? Программа Recognition (перевод с англ. признание) – это инновационный продукт на международном образовательном рынке.
Что такое Recognition? Программа Recognition (перевод с англ. признание) – это инновационный продукт на международном образовательном рынке.  Презентация на тему Петр I
Презентация на тему Петр I  Единое и расчлененное знание в истории культуры
Единое и расчлененное знание в истории культуры 2_5390911506760081685
2_5390911506760081685 Государственный Фонд развития промышленности Рязанской области (ГФРП РО)
Государственный Фонд развития промышленности Рязанской области (ГФРП РО) Некоторые задачи планирования сети магистрального оператора
Некоторые задачи планирования сети магистрального оператора Жизнь и творчество Л.Н. Толстого (1828-1910)
Жизнь и творчество Л.Н. Толстого (1828-1910) Трансплантация
Трансплантация Разработка продающего сайта
Разработка продающего сайта Литература и искусство эпохи Возрождения
Литература и искусство эпохи Возрождения Слайд только для инструкторов *** Не демонстрировать во время презентации
Слайд только для инструкторов *** Не демонстрировать во время презентации МОУ МАГАНСКАЯ СОШ
МОУ МАГАНСКАЯ СОШ Эко-отель Leaprus
Эко-отель Leaprus Презентация на тему Три состояния вещества Физика 7 класс
Презентация на тему Три состояния вещества Физика 7 класс  Клеточное строение корня (1)
Клеточное строение корня (1) Административные дела (первая инстанция) Урок 3.2. Рассмотрение административного дела
Административные дела (первая инстанция) Урок 3.2. Рассмотрение административного дела Зразы картофельные с грибами (замороженный полуфабрикат)
Зразы картофельные с грибами (замороженный полуфабрикат) Внедрение ГШИС и КМИС КУ в образовательном учреждении
Внедрение ГШИС и КМИС КУ в образовательном учреждении Правописание суффиксов -чик- и -щик-
Правописание суффиксов -чик- и -щик- Тест "Про кошек и собак" 2 класс
Тест "Про кошек и собак" 2 класс Смертная казнь по законодательству Республики Казахстан: история и современность
Смертная казнь по законодательству Республики Казахстан: история и современность Первый питательный крем от Anew - Ультра-Питание
Первый питательный крем от Anew - Ультра-Питание