Содержание
- 2. “Все известные вещи имеют число. Без этого ничего нельзя было бы ни мыслить, ни знать” Пифагор
- 3. Рассказывают, что великий геометр, открыв НЕСОИЗМЕРИМОСТЬ сторон квадрата и его диагонали, увидел в том божественный знак,
- 4. Представления чисел пифагорейцами
- 5. Главным открытием Пифагора был прямоугольный равнобедренный треугольник, возникающий в квадрате, где проведена диагональ.
- 6. Нетрудно сказать: какую бы часть стороны квадрата мы ни взяли - половину, четверть, треть и т.п.
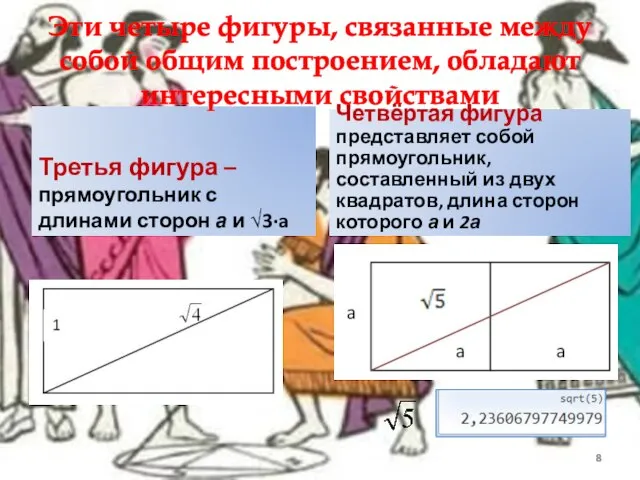
- 7. Эти четыре фигуры, связанные между собой общим построением, обладают интересными свойствами Первая фигура — квадрат —
- 8. Третья фигура – прямоугольник с длинами сторон а и √3∙a Четвёртая фигура представляет собой прямоугольник, составленный
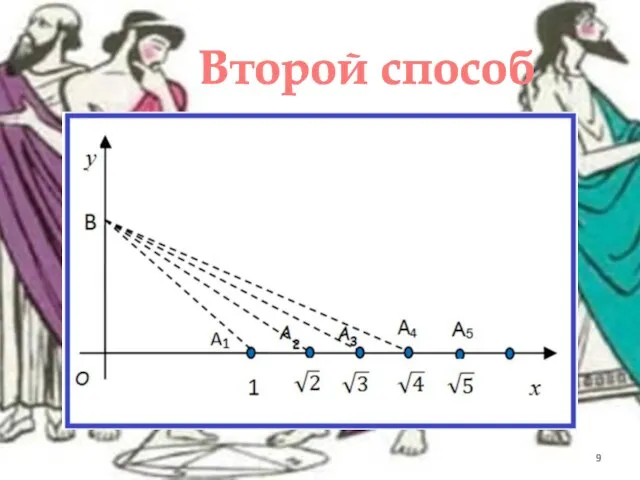
- 9. Второй способ
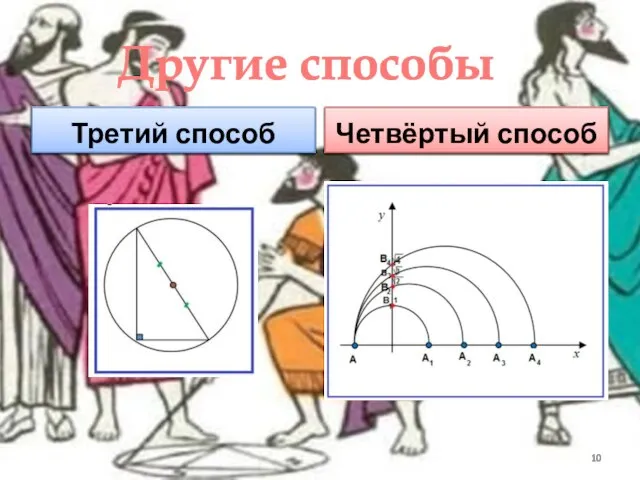
- 10. Третий способ Четвёртый способ Другие способы
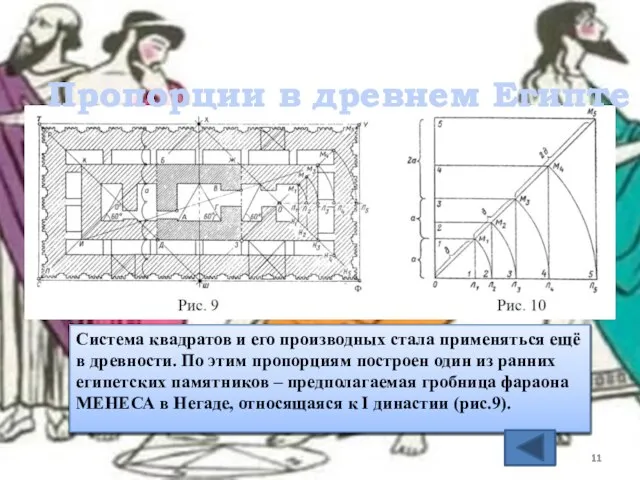
- 11. Система квадратов и его производных стала применяться ещё в древности. По этим пропорциям построен один из
- 13. Скачать презентацию






 Учебно-методический семинар «Проблемы перехода на федеральные государственные образовательные стандарты (ФГОС)третьего поколе
Учебно-методический семинар «Проблемы перехода на федеральные государственные образовательные стандарты (ФГОС)третьего поколе Регенерация
Регенерация Фашизм и тоталитарные режимы
Фашизм и тоталитарные режимы Презентация на тему Европейский Север Факторы формирования района
Презентация на тему Европейский Север Факторы формирования района Сравнение отрезков
Сравнение отрезков Презентация на тему: Построим корабль
Презентация на тему: Построим корабль Содержание воспитания, образования, обучения
Содержание воспитания, образования, обучения Памятники религиозных культур в городе томске
Памятники религиозных культур в городе томске Возрастной макияж
Возрастной макияж  Тюнинг NGINX
Тюнинг NGINX Тест по литературе в 6 классе: Иван Сергеевич Тургенев "Муму"
Тест по литературе в 6 классе: Иван Сергеевич Тургенев "Муму" Зимние игры, направленные на развитие сильной, целенаправленной воздушной струи
Зимние игры, направленные на развитие сильной, целенаправленной воздушной струи Права ребёнка в семье
Права ребёнка в семье Добывающий и очистной модуль железнодорожного комплекса
Добывающий и очистной модуль железнодорожного комплекса Опыт внедрения АИАС «АВЕРС: УПРАВЛЕНИЕ ДОУ»
Опыт внедрения АИАС «АВЕРС: УПРАВЛЕНИЕ ДОУ» Наука и образование
Наука и образование Тема внеклассного мероприятия «12 апреля - День космонавтики»
Тема внеклассного мероприятия «12 апреля - День космонавтики» Философия, её смысл, функции и роль в обществе
Философия, её смысл, функции и роль в обществе Общешкольное мероприятие «Олимпиаде в Сочи быть!»Разработал:Учитель музыки высшей категории Мороз Ирина ВладиславовнаМОУ СОШ
Общешкольное мероприятие «Олимпиаде в Сочи быть!»Разработал:Учитель музыки высшей категории Мороз Ирина ВладиславовнаМОУ СОШ Остров мечты
Остров мечты Trip to UK
Trip to UK Спаситель Петербурга
Спаситель Петербурга БЦ Карма Кагью Якутск
БЦ Карма Кагью Якутск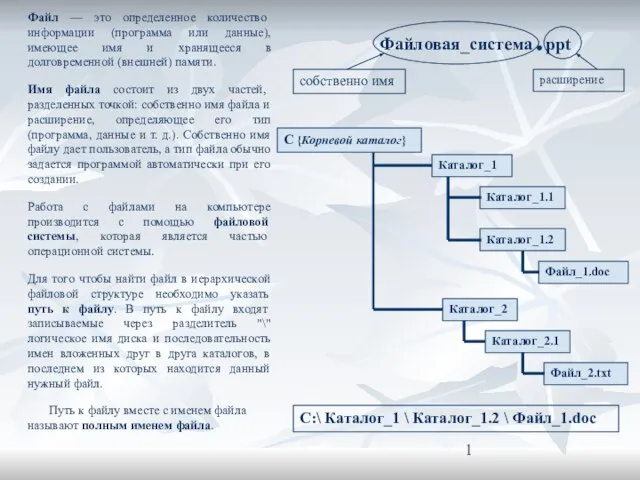 С:\ Каталог_1 \ Каталог_1.2 \ Файл_1.doc
С:\ Каталог_1 \ Каталог_1.2 \ Файл_1.doc Транспозитор спектра, использующего принцип сжатия сигнала во времени для устройств сигнализации об опасности
Транспозитор спектра, использующего принцип сжатия сигнала во времени для устройств сигнализации об опасности Презентация на тему Культура Древней Греции
Презентация на тему Культура Древней Греции Программа кандидата в председатели Студенческого совета МГЛУ
Программа кандидата в председатели Студенческого совета МГЛУ Дружок
Дружок