Содержание
- 2. Цель Снятие перегрузки. Выделение главного.
- 3. В записях рассуждений я использую экономную форму: повторяющиеся слова записываю лишь один раз
- 4. Нахождение неизвестного члена пропорции Правило: 1)
- 5. 2) k x
- 6. Сравнение обыкновенных дробей Из двух дробей с равными числителями та, у которой знаменатель
- 7. ,если a B >
- 8. Переместительные законы сложения и умножения слагаемых множителей От перестановки Сумма произведение Не изменяется
- 10. умножение и деление многочлена на число. Чтобы многочлен на число, достаточно на это число каждый член
- 11. Арифметическая и геометрическая прогрессии. 1. Даны последовательности: 3, 5, 7 … 1, 2, 4, 8 …
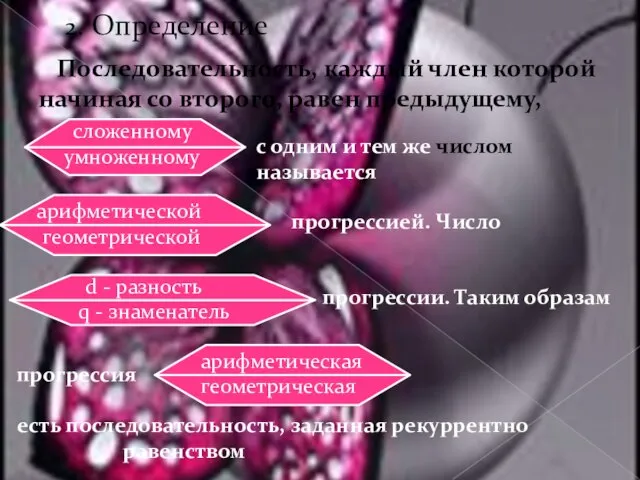
- 12. 2. Определение Последовательность, каждый член которой начиная со второго, равен предыдущему, с одним и тем же
- 14. 3. Свойства Формула n – го члена Что надо знать, чтобы задать прогрессию? её первый член
- 15. Формула n – го члена для арифметической прогрессии: а = а₁+d(n +1) Формула n –го члена
- 16. Характеристическое свойство Последовательность является прогрессией тогда, когда любой её член, начиная со второго, является средним соседних
- 17. Свойство прямой и обратной пропорциональностей. Если две величины пропорциональны, то отношение двух произвольно взятых значений одной
- 18. Установление взаимосвязи между понятиями
- 21. Скачать презентацию






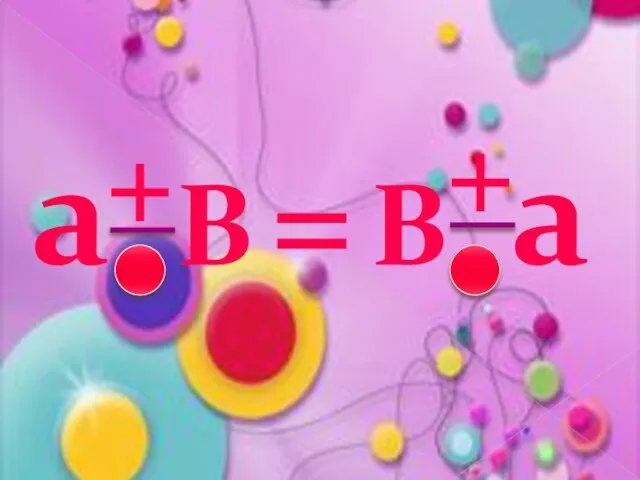


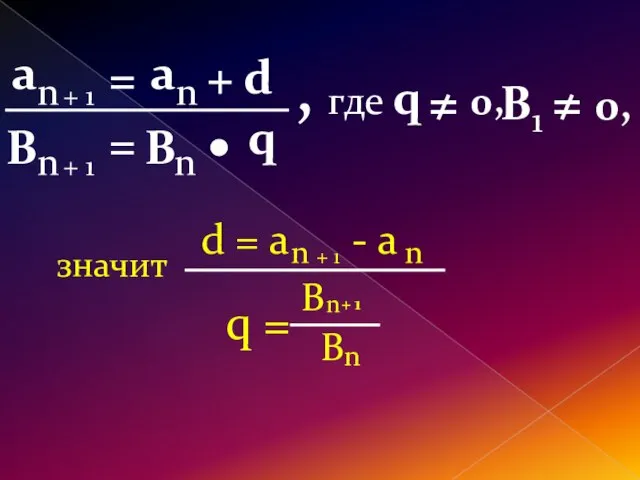






 Роль физической культуры и спорта в нашей жизни
Роль физической культуры и спорта в нашей жизни Джеймс Олдридж
Джеймс Олдридж Соли аммония
Соли аммония Романовская игрушка
Романовская игрушка Построение автоматов
Построение автоматов Перевозка детей на воздушном транспорте
Перевозка детей на воздушном транспорте 1 Художній твір як явище мистецтва, новий ірреальний
1 Художній твір як явище мистецтва, новий ірреальний Сопровождение региональных инновационных площадок в 2022 году
Сопровождение региональных инновационных площадок в 2022 году Структура книги
Структура книги Котёл низкого давления
Котёл низкого давления Оставьте цветы весне
Оставьте цветы весне Презентация на тему Стресс, стрессовое состояние
Презентация на тему Стресс, стрессовое состояние  Актуальность, проблемы и перспективы развития профессионального признания в России Владивосток 2011
Актуальность, проблемы и перспективы развития профессионального признания в России Владивосток 2011 СИЛА ТОКА Кл t А q ЗАРЯД Дж U U q НАПРЯЖЕНИЕ А I I t РАБОТА с А q t ВРЕМЯ В q.
СИЛА ТОКА Кл t А q ЗАРЯД Дж U U q НАПРЯЖЕНИЕ А I I t РАБОТА с А q t ВРЕМЯ В q. Обязательства и ответственность по правам человека
Обязательства и ответственность по правам человека Учебные вопросы: Техника скоростной записи слов и предложений. Применение цветных ручек и карандашей при конспектировании
Учебные вопросы: Техника скоростной записи слов и предложений. Применение цветных ручек и карандашей при конспектировании Упражнения для мышц брюшного пресса (юноши)
Упражнения для мышц брюшного пресса (юноши) Вычисление площади криволинейной трапеции
Вычисление площади криволинейной трапеции Машиностроительное черчение
Машиностроительное черчение Хакасия – моя Родина!
Хакасия – моя Родина! Презентация на тему Как вести себя во время теракта
Презентация на тему Как вести себя во время теракта Мониторинг Active Session History c использованием ASH Viewer
Мониторинг Active Session History c использованием ASH Viewer История моды 20 века
История моды 20 века Союз поисковых отрядов
Союз поисковых отрядов Промоакции и их роль в продвижении товаров
Промоакции и их роль в продвижении товаров Christmas what are they doing fun
Christmas what are they doing fun Олимпийские игры
Олимпийские игры Как правильно передвигаться по загородной дороге?
Как правильно передвигаться по загородной дороге?