в одной и тоже точке, под влиянием различных условий.
Формула производной встречается нам ещё в 15 веке. Великий итальянский математик Тартальи, рассматривая и развивая вопрос - на сколько зависит дальность полёта снаряда от наклона орудия - применяет её в своих трудах.
Формула производной часто встречается в работах известных математиков 17 века. Её применяют Ньютон и Лейбниц.
Посвящает целый трактат о роли производной в математике известный учёный Галилео Галилей. Затем производная и различные изложения с её применением стали встречаться в работах Декарта, французского математика Роберваля и англичанина Грегори. Большой вклад по изучению производной внесли такие умы, как Лопиталь, Бернулли, Лангранж и др.
Применение производной в математике


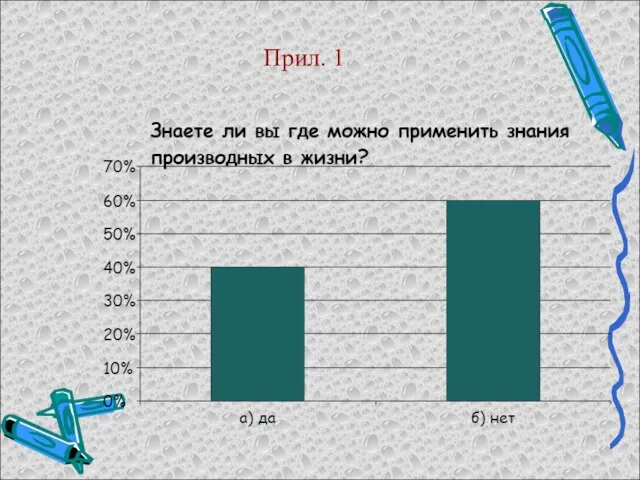
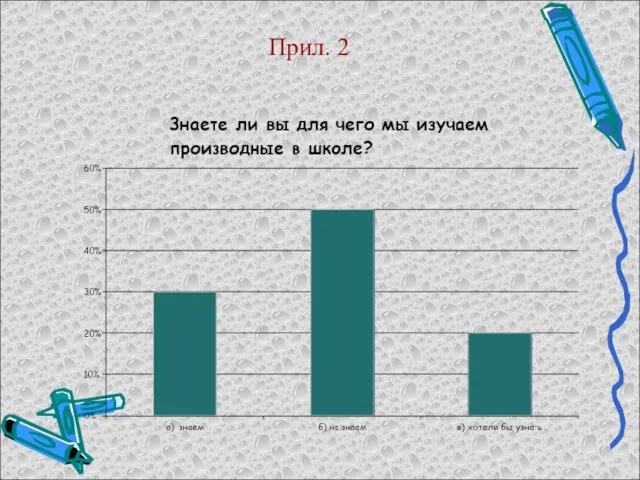


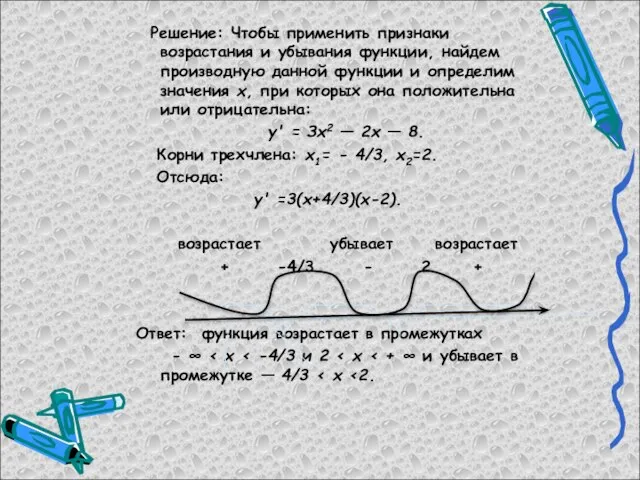




 Опасные места
Опасные места 20140317_merzlikinaip_doc
20140317_merzlikinaip_doc ВИЧ и СПИД
ВИЧ и СПИД Анатомия
Анатомия Электронный документооборот как инструмент борьбы с бюрократией
Электронный документооборот как инструмент борьбы с бюрократией Винсент Виллем ван Гог
Винсент Виллем ван Гог Как выполнить выгрузкуотчетности в электронном виде из программ системы 1С:Предприятие
Как выполнить выгрузкуотчетности в электронном виде из программ системы 1С:Предприятие Преобразования фигур в пространстве
Преобразования фигур в пространстве Предельные одноосновные карбоновые кислоты. Сложные эфиры
Предельные одноосновные карбоновые кислоты. Сложные эфиры Дизайн. Коллаборация. Цифровые технологии. Кейс №3 Перерождение одного изделия в другое
Дизайн. Коллаборация. Цифровые технологии. Кейс №3 Перерождение одного изделия в другое Презентация на тему ДЕЙСТВИЕ ТАБАКА НА ОРГАНИЗМ ЧЕЛОВЕКА
Презентация на тему ДЕЙСТВИЕ ТАБАКА НА ОРГАНИЗМ ЧЕЛОВЕКА  Where is the dog?
Where is the dog? . 1)Прочитать числа: 509, 6001, 90050, 7000850127, 620022. Назвать в каждом из чисел цифру в разряде десятков, сотен. Какие из чисел меньше 1000? 2)Найти
. 1)Прочитать числа: 509, 6001, 90050, 7000850127, 620022. Назвать в каждом из чисел цифру в разряде десятков, сотен. Какие из чисел меньше 1000? 2)Найти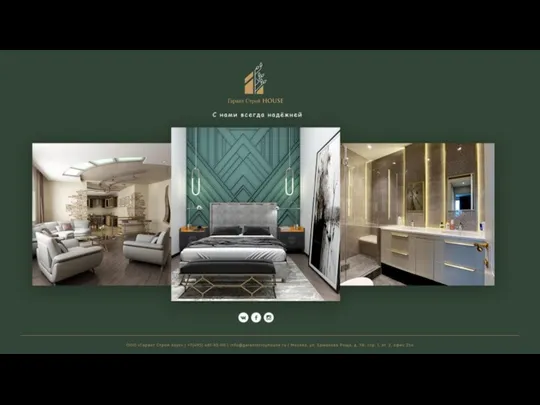 ООО ГарантСтройХаус
ООО ГарантСтройХаус Пончики Пончкофф (фотографии)
Пончики Пончкофф (фотографии) Определение культуры. Типы культур
Определение культуры. Типы культур Искусства бумагокручения
Искусства бумагокручения Технологический процесс ручной дуговой сварки листовых конструкций из стали (ст-3пс)
Технологический процесс ручной дуговой сварки листовых конструкций из стали (ст-3пс) МЫ СКОРО УЙДЁМ СО ШКОЛЬНОГО ДВОРА…
МЫ СКОРО УЙДЁМ СО ШКОЛЬНОГО ДВОРА… Эффективные приёмы запоминания учебного материала
Эффективные приёмы запоминания учебного материала Административно-правовой статус
Административно-правовой статус Развитие личности младшего школьника средствами учебного диалога
Развитие личности младшего школьника средствами учебного диалога БЭК-ОФИС СОЗДАНИЕ, РАЗВИТИЕ, АВТОМАТИЗАЦИЯ
БЭК-ОФИС СОЗДАНИЕ, РАЗВИТИЕ, АВТОМАТИЗАЦИЯ Внеурочная работа по математике
Внеурочная работа по математике Слайды
Слайды ГОГОЛЬ: знакомый и незнакомый
ГОГОЛЬ: знакомый и незнакомый The Cable News Network
The Cable News Network Сила. Основы методики ее воспитания
Сила. Основы методики ее воспитания