Содержание
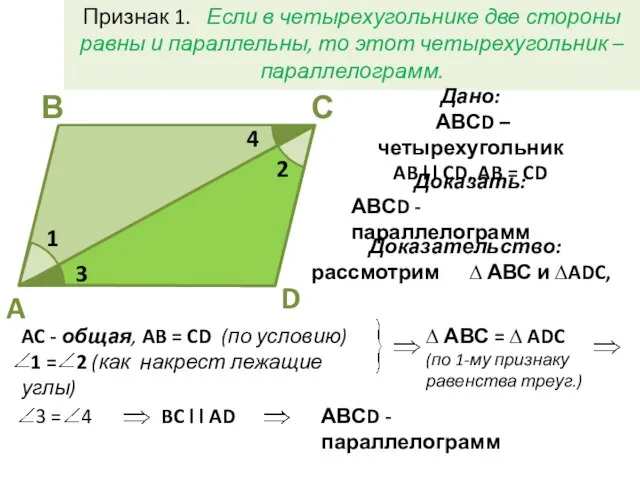
- 2. Признак 1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм. С
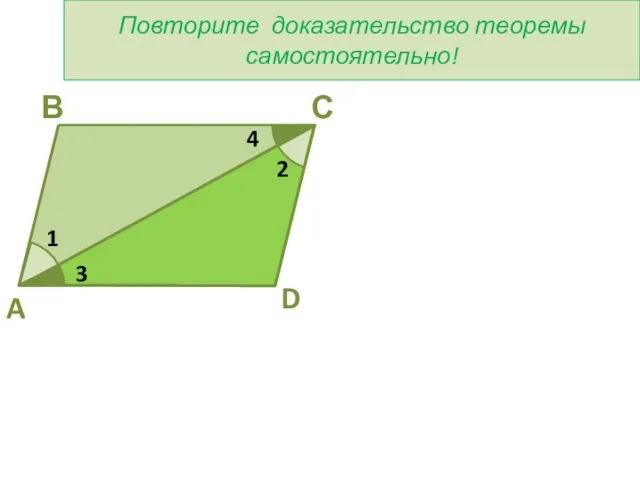
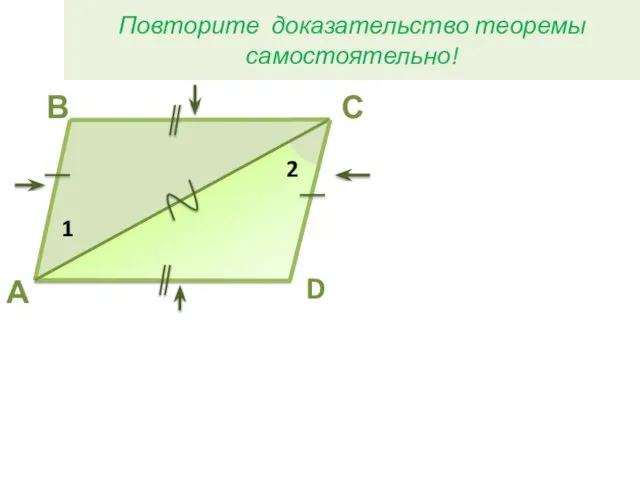
- 3. С В D A 2 1 4 3 Повторите доказательство теоремы самостоятельно!
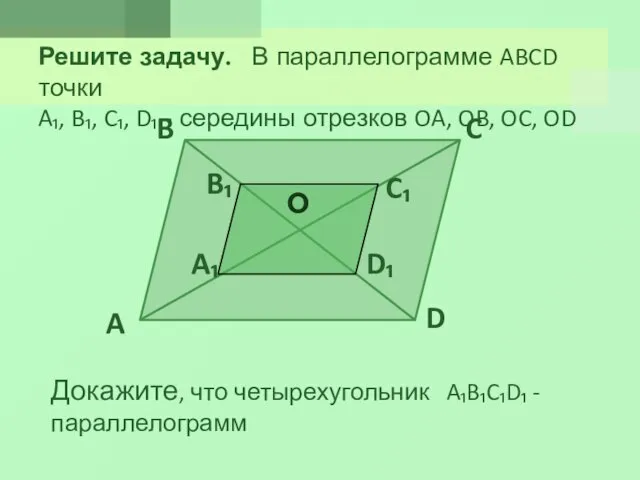
- 4. Решите задачу. В параллелограмме ABCD точки A₁, B₁, C₁, D₁ - середины отрезков OA, OB, OC,
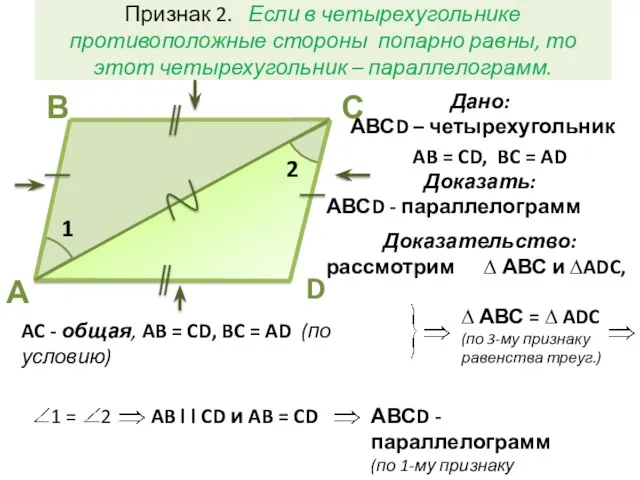
- 5. Признак 2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм. D С
- 6. D С В А 1 2 Повторите доказательство теоремы самостоятельно!
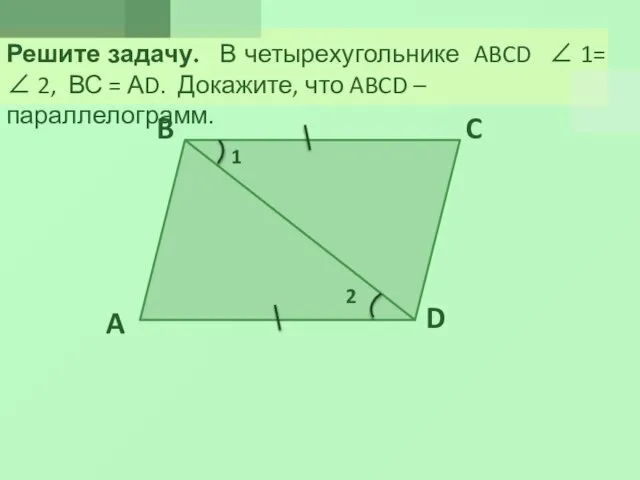
- 7. Решите задачу. В четырехугольнике ABCD 1= 2, ВС = АD. Докажите, что ABCD –
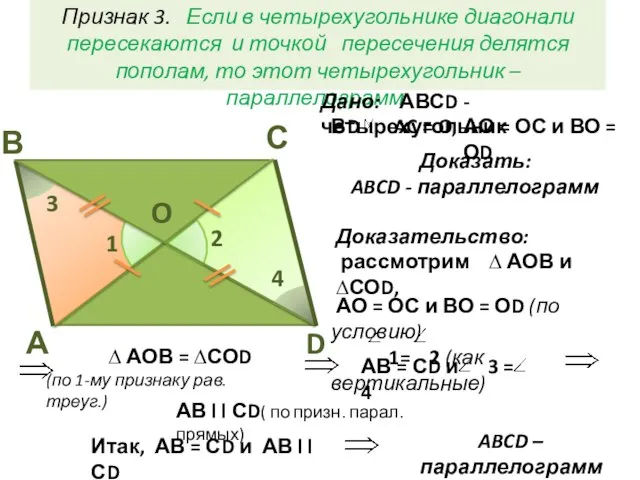
- 8. АВ = СD и 3 = 4 АО = ОС и ВО = ОD (по условию)
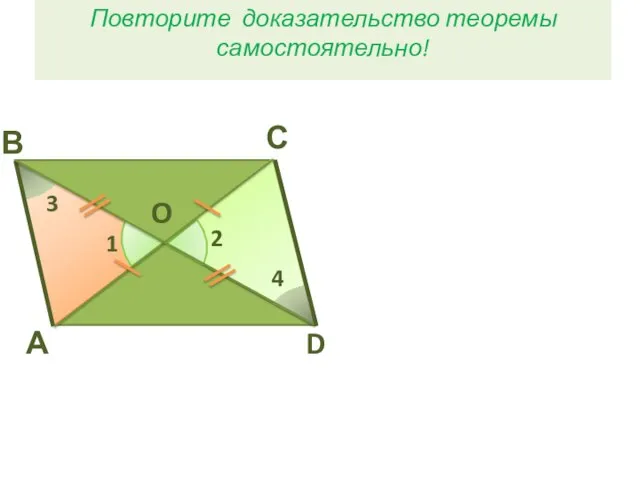
- 9. В А С D O 3 1 2 4 Повторите доказательство теоремы самостоятельно!
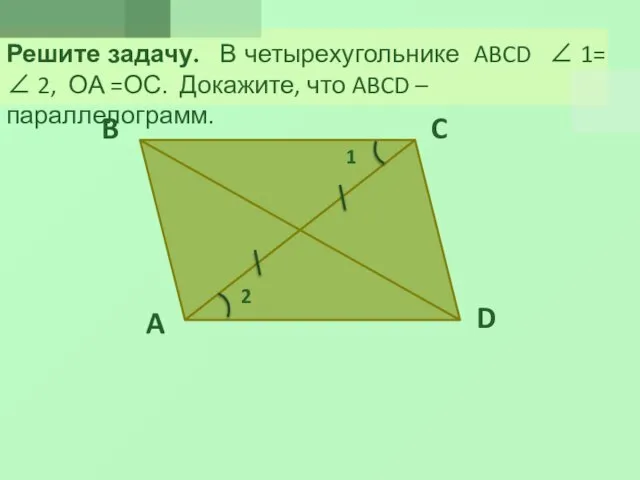
- 10. Решите задачу. В четырехугольнике ABCD 1= 2, ОА =ОС. Докажите, что ABCD – параллелограмм.
- 12. Скачать презентацию
 Презентация на тему Виды транспортных средств
Презентация на тему Виды транспортных средств  Родительское собрание по теме:« Как помочь ребенку стать внимательным»
Родительское собрание по теме:« Как помочь ребенку стать внимательным» Корпорации и НКО – трудности перевода
Корпорации и НКО – трудности перевода Дополнения к методике работы проверяющего вакцинопрофилактики
Дополнения к методике работы проверяющего вакцинопрофилактики www.editorsweblog.ru
www.editorsweblog.ru Ко дню собора казанских святых. Удивительные факты единства православных святых земли Казанской, связанной с Пермской землей
Ко дню собора казанских святых. Удивительные факты единства православных святых земли Казанской, связанной с Пермской землей 20140214_moy_predmet_v_sisteme_obrazovaniya
20140214_moy_predmet_v_sisteme_obrazovaniya Экспериментальная огневая отработка жидкостных ракетных двигателей малых тяг на стенде МАИ
Экспериментальная огневая отработка жидкостных ракетных двигателей малых тяг на стенде МАИ Мстительное путешествие во времени
Мстительное путешествие во времени Les nombres en français
Les nombres en français Негде в тридевятом царстве, в тридесятом государстве…
Негде в тридевятом царстве, в тридесятом государстве… Electronic interactive student’s calendar
Electronic interactive student’s calendar Борис Ельцин
Борис Ельцин Презентация на тему Урок чтения и развития речи в 1 классе
Презентация на тему Урок чтения и развития речи в 1 классе  Производство хлорида калия
Производство хлорида калия Психология как наука
Психология как наука Сағындым бауырымды
Сағындым бауырымды Научная работа по физикена тему«Влияние влажности воздуха на самочувствие человека»
Научная работа по физикена тему«Влияние влажности воздуха на самочувствие человека» Презентация на тему "Ацетилсалициловая кислота" - скачать презентации по Медицине
Презентация на тему "Ацетилсалициловая кислота" - скачать презентации по Медицине 03. Органи. Фізіологічні системи
03. Органи. Фізіологічні системи Загадки Даля
Загадки Даля Слоаврь
Слоаврь Азия (2 класс)
Азия (2 класс) Анализ и совершенствование деятельности Администрации Уватского муниципального района
Анализ и совершенствование деятельности Администрации Уватского муниципального района Великие открытия людей
Великие открытия людей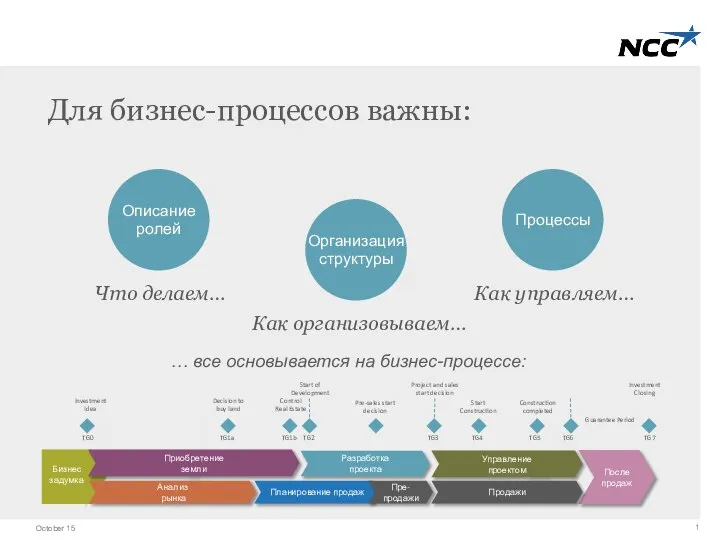 Бизнес-процессы. 1часть
Бизнес-процессы. 1часть Компьютер и человек, вред или здоровье???
Компьютер и человек, вред или здоровье??? Примеры реконструируемых зданий
Примеры реконструируемых зданий