Проблема сужения множества Парето и подходы к ее решению

Содержание
Исторические аспекты
Постановка задачи многокритериального выбора
Принцип Эджворта-Парето
Эвристические методы поиска «наилучшего» решения
Основы аксиоматического подхода к решению проблемы сужения множества Парето
Современное состояние аксиоматического подхода
Литература

Истоки
J. Borda (1871)
M. Condorcet (1785)
F. Edgeworth (1881)
V. Pareto (1906)

Постановка задачи многокритериального выбора
(в терминах решений)
ЗМКВ: 〈X, f, PX〉
X – множество возможных решений
f =(f1,…,fm) – векторный критерий
PX – бинарное отношение строгого предпочтения ЛПР, заданное на X; т.о. xPX x‘ означает, что x предпочтительнее x‘
C(X) (Sel(X)) – множество выбираемых решений
C(X) ⊂ X

Постановка задачи многокритериального выбора
(в терминах векторов)
ЗМКВ: 〈Y, PY 〉
Y = f(X) – множество возможных векторов
PY – отношение строгого предпочтения на Y
xPX x‘ ↔ yPY y‘ , где y = f(x), y‘ = f(x‘)
C(Y) (Sel(Y)) – множество выбираемых векторов
C(Y) = f(C(X)) ⊂ Y

Множество Парето
Pf(X) = {x*∈X| не существует x*∈X : f(x) ≥ f(x*)}
P(Y) = {y*∈Y | не существует y*∈Y : y ≥ y*}
y ≥ y* ↔ yi ≥ yi* , i=1,…,m; y ≠ y*
P(Y) = f(Pf(X))

Аксиомы «разумного» выбора
Аксиома 1 ( аксиома исключения доминируемых векторов)
y1 , y2 ∈ Y : y1 PY y2 ⇒ y2 ∉ C(Y).
Аксиома 2 (аксиома Парето):
y1 , y2 ∈ Y : y1 ≥ y2 ⇒ y1 PY y2.

Принцип Эджворта-Парето
Предположим, что в процессе выбора ЛПР следует аксиоме Парето. Тогда для любого множества выбираемых им векторов C(Y), подчиненного аксиоме 1, имеет место включение
С(Y) ⊂ P(Y)

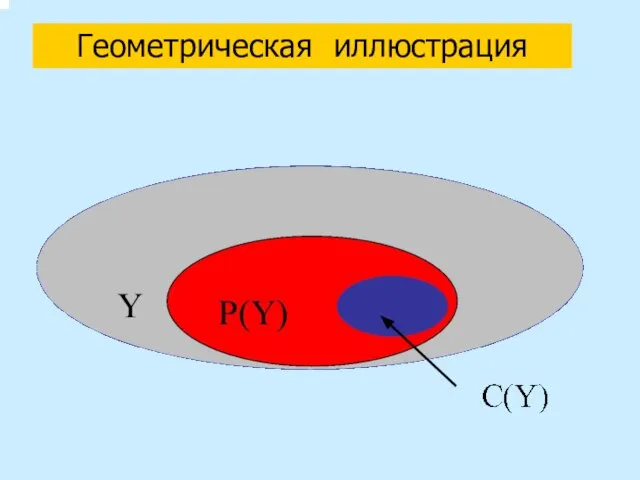
Геометрическая иллюстрация

Выводы
1. Если ЛПР выбирает хотя бы один вектор за пределами множества Парето P(Y), то оно игнорирует по крайней мере одну из аксиом 1 − 2.
2. Если хотя бы одна аксиома 1 или 2 не принимается, то выбираемый вектор не обязательно должен быть парето-оптимальным.
3. Если используется какой-либо метод выбора того или иного парето-оптимального вектора, то обязательно следует предполагать выполненными обе аксиомы 1 – 2.

Эвристические методы отыскания «наилучшего» решения
Методы ранжирования (J. Borda, M.Condorcet, A. Copeland), МАИ (T. Saaty), ELECTRE (B. Roy), MACBETH (J. Brans)
Методы, основанные на построении функции ценности (R. Keeney, H. Raiffa, P. Fishburn)
Методы скаляризации
Целевое программирование
Лексикографическая оптимизация
Человеко-машинные процедуры

Методология сужения множества Парето
Гафт М.Г., Озерной В.М.
Подиновский В.В. и Вик.В.
Ларичев О.И.
Ногин В.Д.
Берман В.П., Наумов Г.Е.
Барышников Ю.М., Березовский Б.А., Борзенко В.И., Кемпнер Л.М.

Свойство произвольной пары парето-оптимальных векторов
Пусть Y ⊂ Rm. Для любых двух векторов y,y’∈ P(Y) существуют два непустых непересекающихся множества номеров критериев A,B ⊂ {1,2,,…,m} , таких, что
1) yi > y’i для всех i ∈ A
2) y’j > yj для всех j ∈ B
3) ys = y’s для всех остальных s (если они найдутся)

«Квант» информации
Самый простой способ сужения множества Парето – это исключение какого-то одного вектора из пары парето-оптимальных векторов после их сравнения;
иначе говоря, − предпочтение одного парето-оптимального вектора другому, т.е.
y PY y’, где y, y’ ∈ P(Y).
Будем говорить, что подобное предпочтение составляет некий «квант» информации об отношении строгого предпочтения PY ЛПР.

Развитие идеи
Для того чтобы сужение было «заметным» необходимо ограничить рассмотрение таким классом задач многокритериального выбора, в котором поступление одного указанного «кванта» информации приводило бы к удалению сразу целого ряда других парето-оптимальных векторов.
Существует несколько подходов, которые, в сильной степени зависят и от шкал, в которых измеряются значения критериев.

Предположения
Будем считать, что значения критериев измеряются в количественных шкалах (отношений, разности, интервалов).
Рассматриваемый класс задач ограничим набором из определенных 4 аксиом «разумного» поведения ЛПР в процессе выбора решений.

Аксиомы «разумного» выбора
Исключение доминируемых векторов
Транзитивность отношения предпочтения
Согласованность отношения предпочтения с критериями
Инвариантность отношения предпочтения относительно положительного линейного преобразования

Оценка сверху
При выполнении аксиом 2-4 неизвестное отношение PY строгого предпочтения ЛПР является конусным с острым выпуклым конусом.
Получение «кванта» информации дает возможность выделить некоторую «часть» отношения PY, с помощью которой можно построить определенную оценку сверху P^(Y) для неизвестного множества выбираемых векторов: C(Y) ⊂ P^(Y) ⊂ P(Y)
где P^(Y) = f(Pf^(X)).

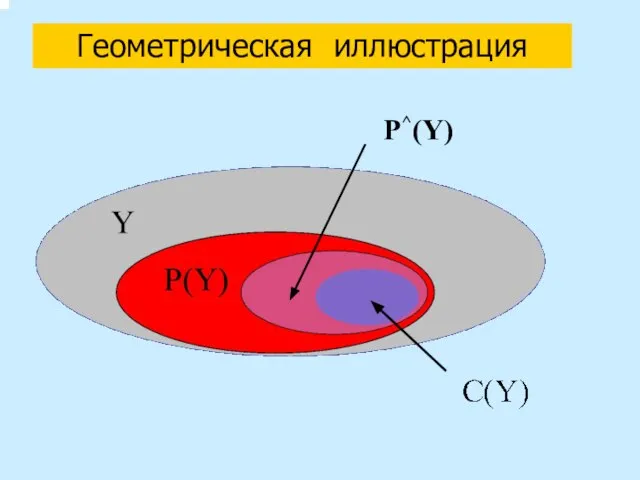
Геометрическая иллюстрация
P^(Y)

Построение «нового» критерия
Новый критерий f^ отличается от «старого» f лишь компонентами группы B:
f0^(x) = min { fi(x)/wi | i∈A } + min { fj(x)/wj | j∈B }
fij^(x) = fi(x)/wi + fj(x)/wj для всех i∈A, j ∈ B
где
wi = yi − y’i , wj = y’j − yj .

Использование набора «квантов» информации
Получены условия непротиворечивости подобной информации.
В случае конечного Y разработан алгоритм построения оценки сверху
Для бесконечного Y есть ряд результатов, но в общем случае решения нет. Задача выпуклого анализа.

Полнота конечного набора «квантов» информации
Доказано, что с помощью конечного непротиворечивого набора «квантов» информации можно получить сколь угодно точную оценку сверху для неизвестного множества недоминируемых векторов
Ndom(Y) = { y*∈Y | не существует y∈Y: y Py y* }

Обобщение и развитие
Более общие шкалы для измерения значений критериев
Нечеткое отношения предпочтения PY и/или нечеткое множество Y
Использование функций выбора (в том числе и нечеткой) и общей модели теории выбора вариантов
Решение прикладных задач

Персональная страница в Интернет
На русском языке:
http://www.apmath.spbu.ru/ru/staff/nogin
На английском языке:
http://www.apmath.spbu.ru/en/staff/nogin

Литература
Айзерман М.А., Алескеров Ф.Т. Выбор вариантов. Основы теории. – М.: Наука, 1990, 236 с.
Березовский Б.А., Барышников Ю.М., Борзенко В.И., Кемпнер Л.М. Многокритериальная оптимизация. Математические аспекты. – М.: Наука, 1989, 128 с.
Берман В.П., Наумов Г.Е. Отношение предпочтения с интервальным коэффициентом замещения// Автоматика и телемеханика, 1989, 3 3, С. 139-153.
Гафт М.Г. Принятие решений при многих критериях. М.: Знание, 1979.
Гафт М.Г., Подиновский В.В. О построении решающих правил в задачах принятия решений // Автоматика и телемеханика. 1981. № 6. С. 128 – 138.
Гермейер Ю.Б. Введение в теорию исследования операций, М.: Наука, 1971.
Кини Р.Л., Райфа Х. Принятие решений при многих критериях: предпочтения и замещения. − М.: Радио и связь, 1981.
Климова О.Н., Ногин В.Д. Учет взаимно зависимой информации об относительно1й важности критериев в процессе принятия решений// Журнал вычислительной математики и математической физики, 2006, т. 46, № 7, С. 2179-2191.

Литература
Ларичев О.И. Наука и искусство принятия решений. – М.: Наука, 1979.
Ларичев О.И. Теория и методы принятия решений. М.: Логос, 2000.
Меньшикова О.Р., Подиновский В.В. Построение отношения предпочтения и ядра в многокритериальных задачах с упорядоченными по важности неоднородными критериями// ЖВМиМФ, 1988, 28(5), 647-659.
Миркин Б.Г. Проблема группового выбора. М.: Наука, 1974.
Ногин В.Д. Новый способ сужения области компромиссов// Известия АН СССР. Техническая кибернетика, 1976, 5.
Ногин В.Д. и др. Основы теории оптимизации. – М.: Высшая школа, 1986, 384 с.
Ногин В.Д. Теоремы о полноте в теории относительной важности критериев// Вестник СПбГУ, сер.: мат., мех., астрономия., 2000, 40 (25), 13-18.
Ногин В.Д. Логическое обоснование принципа Эджворта-Парето// Журнал вычислительной математики и математической физики, 2002, т. 42, № 7, С. 950-956.

Литература
Ногин В.Д. Принятие решений в многокритериальной среде: количественный подход. М.: Физматлит, 2005, 2-е изд.
Ногин В.Д. Принцип Эджворта-Парето и относительная важность критериев в случае нечеткого отношения предпочтения// Журнал вычислительной математики и математической физики, 2003, т. 43, № 11, с. 1676-1686.
Ногин В.Д. Обобщенный принцип Эджворта-Парето и границы его применимости// Экономика и математические методы, 2005, т. 41, № 3, С. 128-134.
Ногин В.Д. Принцип Эджворта-Парето в терминах нечеткой функции выбора// Журнал вычислительной математики и математической физики, 2006, т. 46, № 4, С. 582-591.
Ногин В.Д., Волкова Н.А. Эволюция принципа Эджворта-Парето// Таврический вестник информатики и математики, 2006, № 1, С. 21-33.

Литература
Озерной В.М., Гафт М.Г. Методологи решения дискретных многокритериальных задач // Многокритериальные задачи принятия решений. М.: Машиностроение. 1978. С. 14 – 47.
Подиновский В.В. Многокритериальные задачи с однородными и равноценными критериями// ЖВМиМФ, 1975, 15 (2), 330-334.
Подиновский В.В. Многокритериальные задачи с упорядоченными по важности критериями // Автоматика и телемеханика, 1976, 2, 118-127.
Подиновский В.В. Об относительной важности критериев в многокритериальных задачах принятия решений // Многокритериальные задачи принятия решений. М.: Машиностроение. 1978. С. 48 – 82.
Подиновский В.В. Принцип гарантированного результата для частичных отношений предпочтения // Журнал вычислительной математики и математической физики. 1979. Т. 19. № 6. С. 1436 – 1450.
Подиновский В.В. Аксиоматическое решение проблемы оценки важности критериев в многокритериальных задачах принятия решений // Современное состояние теории исследования операций. М.: Наука, 1979. С. 117 – 149.

Литература
Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач. − М.: Наука, 1982, 255 с.
Салуквадзе М.Е. О задаче линейного программирования с векторным критерием качества// Автоматика и телемеханика, 1972, 5, 99-105.
Фишберн П. Теория полезности для принятия решений. М.: Наука, 1978, 352 с.
Berman V.P., Naumov G. E. Podinovski V.V. Interval value tradeoffs methodology and techniques of multi-criteria decision analysis. In User-oriented methodology and techniques of decision analysis and support. Springer-Verlag, Berlin, 1993, P. 144-149.
Charns A., Cooper W.W., Ferguson R.O. Optimal estimation of execute compensation by linear programming// Management Science, 1955, 1 (2).
Geoffrion A.M., Dyer J.S., Fienberg A. An interactive approach for multi-criterion optimization, with an application to the operation of an academic department// Management Science, 1972, v. 19, No. 4, Part 1.
Figueira J., Greco S., Ehrgott M. Multiple criteria decision analysis: state of the art surveys. Springer, 2005.

Литература
Miettinen K. Nonlinear multiobjective optimization. Kluver, 1999.
Noghin V.D. Estimation of the set of nondominated solutions// Numerical Functional Analysis and Applications, 1991, 12 (5&6), 507-515.
Noghin V.D. Upper estimate for a fuzzy set of nondominated solutions// Fuzzy Sets and Systems, 1994, 67, 303-315.
Noghin V.D. Relative importance of criteria: a quantitative approach// J. Multi-Criteria Decision Analysis, 1997, 6, 355-363.
Noghin V.D. What is the relative importance of criteria and how to use it in MCDM. - In “Multiple Criteria Decision Making in the New Millenium”, Proceedings of the XV International Conference on MCDM (ed. by M Köksalan, S. Zionts) in Ankara, Turkey (July, 2000), Springer, 2001, pp. 59-68.
Noghin V.D. The Edgeworth-Pareto principle in decision making. Российско-финская школа-семинар «Динамические игры и многокритериальная оптимизация». Сентябрь 2006г., Петрозаводск, Россия. Ресурс ИНТЕРНЕТ: http://www.apmath.spbu.ru/ru/staff/nogin/Edgeworth_Pareto_Principle.pdf