Проект «Методика подготовки учащихся к изучению нового материала по теме: «Системы однородных уравнений»

Цель урока:
Сформировать представление о системах однородных уравнений.
Овладеть умением совершать равносильные преобразования, решая системы однородных уравнений.
Отработать навыки решения систем однородных уравнений с двумя переменными различными методами.

Ход урока
Актуализация опорных знаний:
Проверка домашнего задания (учащиеся выполняют работу на компьютере)
Задание 1
Задание 2
Задание 3
Задание 4

Индивидуальная работа с учащимися.
Карточка 1.
Решить однородное уравнение
x2+4xy-5y2=0
Карточка 2.
Решить однородное уравнение
6х2+11ху-7у2=0

Дополнительные вопросы
Что называют системой уравнений?
Что называют решением системы уравнений
Что значит решить систему уравнений
Алгоритм решения систем уравнений методом подстановки
Алгоритм решения систем уравнений методом алгебраического сложения
Алгоритм решения систем уравнений методом замены переменной

Самостоятельная работа
Вариант 1
(5;2)
(-4;-2,5)
Ответ: (5;2) (-4;-2,5)
Вариант 2
y(-2y+1)=-6
x+2y=1
-2у2+у+6=0
х=-2у+1
2у2-у-6=0
х=-2у+1
у=2
у=-1,5
х=-2у+1
х=-3
у=2
х=4
у=-1,5
(-3;2) (4;-1,5)
Ответ: (-3;2) (4;-1,5)
Решить систему уравнений
х2-у2=16
х+у=2
2(х-у)=16
х+у=2
(х-у)(х+у)=16
х+у=2
(х-у)=8
х+у=2
2х=10
-2у=6
х=5
у=-3
(5;-3)
Ответ: (5;-3)
1)
2)
1)
2)

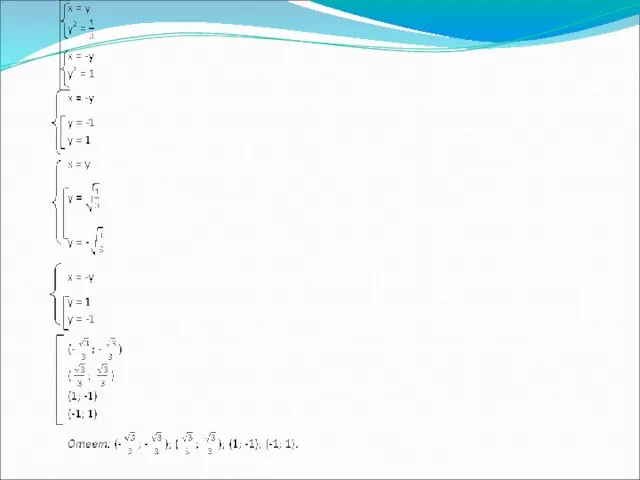
Устная работа
1) (5;-3) (-5;3)
2) (-5;7) (3;-1)
3) (5;-3) (-3;5)
4) (-5;7) (5;-7)
1) Решить систему уравнений
2)Найти значение суммы х + у, если известно, что (х ; у )- решение системы уравнений
1) 4
2) 2
3) -2
4) -4
3) При каких значениях а уравнение х2-6х+а=0 имеет 1 корень?
1) 0
2) 2
3) 9
4) -9
4) Решить квадратное уравнение х2+4х-5=0
1) -5;1
2) 2;3
3) 5;-1
4) -3;2

Объяснение нового материала
Повторить определение однородных уравнений
Дать определение систем однородных уравнений
Рассмотреть системы, содержащие однородные уравнения
Рассмотреть различные методы решения систем однородных уравнений

Однородные уравнения
Многочлен с двумя переменными вида
p(x;y)=anxn+an-1xn-1y+an-2xn-2y2+…a1xyn-1+a0yn, где аn отлично от нуля, называют однородным многочленом n-ой степени с двумя переменными х, у.
Если p(x;y) – однородный многочлен, то уравнение p(x;y) =0 называют однородным уравнением.
Характерный признак однородного многочлена – сумма показателей степеней переменных в каждом члене многочлена одна и та же.

Примеры
P(x,y)=2x+3y – однородный многочлен первой степени; 2x+3y=0 – однородное уравнение первой степени
P(x,y)=3x2+5xy-7y2 – однородный многочлен второй степени; 3x2+5xy-7y2 =0 однородное уравнение второй степени
P(x,y)= x3+4x2y-5y3 – однородный многочлен третьей степени; x3+4x2y-5y3=0 – однородное уравнение третьей степени

Устно
Какие из данных уравнений являются однородными?
x+2y2=3
x3+4x2y-8y3+3xy=0
x2+2xy+3y2=0
4x2-4xy+y=0
x2+xy=0

Тема урока: «Системы однородных уравнений»
Определение.
Система уравнений
называется однородной, если p(x,y), q(x,y) – однородные многочлены, а и b - действительные числа .

Пример решения системы однородных уравнений
x2+4xy-5y2=0 (1)
x2-3xy+4y=0
(1) – однородное уравнение второй степени

3)Решим вторую систему уравнений
х=у
у2-3у2+4у=0
х=у
-2у(у-2)=0
х=у
у=0 (2;2)
у=2 (0;0)
Ответ: (2;2) (0;0) (0,5;-0,1)
Получим:
х = -5у
x2-3xy+4y=0
х = у
x2-3xy+4y=0
2)Решим первую систему уравнений методом подстановки:
х=-5у
25у2+15у2+4у=0
х=-5у
40у2+4у=0
х=-5у
4у(10у+1)=0
х=-5у
у=-0,1 (0;0)
у=0 (0,5; -0,1)
(1)
(2)

№2
х2+3ху=7
у2+ху=6
-6х2-18ху=-42
7у2+7ху=42
-6
7

Если t= , то = , х= у
Если t= , х= у, то
(1;-2)
(-1;2)
Ответ: (-1;2)(1;-2)
ø

Закрепление нового материала
Решить систему уравнений
Решить систему уравнений
Решить систему уравнений

Итоги урока
Ввели понятие системам однородных уравнений и рассмотрели различные методы решения систем.
§12 (стр. 89-91)
№12.07(а), 12.08(б), 12.14(в,г)
Домашнее задание