Прогнозирование на основе использования эконометрических моделей

Что мы знаем:
Спецификация эконометрической модели
Сбор исходной информации
Вычислительный этап:
Оценка параметров модели (теорема Гаусса-Маркова)
4. Анализ полученных результатов:
4.1. Тестирование качества спецификации модели
(коэффициент R2, F-тест, проверка H0: ai=0)
4.2 Исследование модели на мультиколлинеарность

Одно из условий возможности применения МНК – это матрица X должна иметь полный ранг.
Это означает, что все столбцы матрицы коэффициентов системы уравнений наблюдений должны быть линейно-независимыми
Данное условие математически можно записать так:
где: k – число столбцов матрицы Х (Количество регрессоров в модели +1)
Если среди столбцов матрицы Х имеются линейно-зависимые, то rank(X)
Тогда по свойству определителей
(3.1)
(3.2)
ПОНЯТИЕ МУЛЬТИКОЛЛИНЕАРНОСТИ

Условие (3.2) приводит к тому, что матрица (XTX)-1 не существует, то есть является вырожденной.
Следовательно, нет возможности воспользоваться процедурами, сформулированными в теореме Гаусса-Маркова для оценки параметров модели и их ковариационной матрицы.
Наличие линейных (иногда функциональных) связей между факторами X1,X2,....Xk, включенными во множественную эконометрическую модель называется мультиколлинеарностью.
Существует полная и частичная мультиколлинеарности.
Понятие мультиколлинеарности

Если, регрессоры в модели связаны строгой функциональной зависимостью, то говорят о наличии полной (совершенной) мультиколинеарности
Полная мультиколлинеарность не позволяет однозначно оценить параметры исходной модели и разделить вклады регрессоров в эндогенную переменную по результатам наблюдений
Рассмотрим пример
Пусть спецификация модели имеет вид:
(3.3)
Предположим, что регрессоры x1 и x2 связаны между собой строгой линейной зависимостью:
(3.4)
Полная мультиколлинеарность

Подставив (3.4) в (3.3), получим уравнение парной регрессии
Раскрыв скобки и приведя преобразования, получим модель в виде:
(3.5)
Уравнение (3.5) можно записать в виде:
Полная мультиколлинеарность
По оценкам параметров b0 и b1 невозможно однозначно оценить параметры модели (3.3), так как в системе (3.6) неизвестных больше, чем исходных данных. Такая система, в общем случае, имеет бесчисленное множество решений.
(3.6)

Так как в реальности мы имеем дело с данными, имеющими стохастический характер, то случай полной мультиколлинеарности на практике встречается крайне редко.
На практике мы имеем дело с частичной мультиколлинеарностью.
Частичная (несовершенная, стохастическая) мультиколлинеарность характерна для случаев, когда часть экзогенных факторов (X1, X2, …, Xk) находится в корреляционной связи или образовывает различные линейные комбинации вида
Для определения степени коррелированности строят матрицу взаимных корреляций регрессоров R={rij}, I,j=1,2,…,k
Частичная мультиколлинеарность

Если между регрессорами имеется корреляционная связь, соответствующий коэффициент корреляции будет близок к единице rij≈1
Матрица (XTX)-1 будет иметь полный ранг, но близка к вырожденной, т.е det(XTX)-1≈0
В этом случае, формально можно получить оценки параметров модели, их точностные показатели, но все они будут неустойчивыми.
Подобная ситуация возникает, если при спецификации модели в качестве факторных признаков одновременно используются такие показатели, как затраты на единицу продукции, себестоимость товара, его цена.
Частичная мультиколлинеарность

Последствия частичной мультиколлинеарности:
- Увеличение дисперсий оценок параметров. Это расширяет интервальные оценки и снижает их точность;
- Уменьшение значений t-статистик для параметров, что приводит к неправильному выводу о их статистической значимости;
Неустойчивость оценок МНК-параметров и их дисперсий;
Возможность получения неверного (с точки зрения теории) знака у оценки параметра.
Частичная мультиколлинеарность

Поясним это на примере
Пусть спецификация модели имеет вид:
Для такой модели значения дисперсий параметров и их ковариация может быть выражена через значение выборочного коэффициента корреляции следующим образом:
Частичная мультиколлинеарность

Точные количественные критерии для обнаружения частичной мультиколлинеарности отсутствуют.
В качестве признаков ее наличия используют следующие:
- Модуль парного коэффициента корреляции между регрессорами Хi и Xj больше 0,75
- Близость к нулю определителя матрицы (XTX)-1
- Большое количество статистически незначимых параметров в модели
Частичная мультиколлинеарность

ПРИЗНАКИ МУЛЬТИКОЛЛЛИНЕАРНОСТИ
К общим признакам наличия мультиколлинеарности в регрессионной модели следует отнести:
1. Небольшое изменение исходных данных (например, добавление новых наблюдений) приводит к существенному изменению оценок параметров модели;
2. Оценки имеют большие стандартные ошибки и малую значимость в то время как модель в целом является значимой (наблюдается высокое значение коэффициента детерминации и соответствующей F-статистики);
3. Оценки параметров имеют неоправданно большие значения или неверные знаки

СПОСОБЫ ОПРЕДЕЛЕНИЯ НАЛИЧИЯ МУЛЬТИКОЛЛИНЕАРНОСТИ

СПОСОБЫ ОПРЕДЕЛЕНИЯ НАЛИЧИЯ МУЛЬТИКОЛЛИНЕАРНОСТИ

СПОСОБЫ ОПРЕДЕЛЕНИЯ НАЛИЧИЯ МУЛЬТИКОЛЛИНЕАРНОСТИ

СПОСОБЫ ОПРЕДЕЛЕНИЯ НАЛИЧИЯ МУЛЬТИКОЛЛИНЕАРНОСТИ
5. Метод Феррара-Глобера, который основан на применении трех видов статистических критериев:
1) всего массива независимых переменных ( критерий);
2) каждой независимой переменной со всеми другими (F-критерий);
3) каждой пары независимых переменных (t-критерий).
Сравнив эти критерии с их критическими значениями, можно сделать вывод о наличии или отсутствии мультиколлинеарности между независимыми переменными.

ЧАСТНЫЕ КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ
Коэффициент корреляции, очищенный от влияния других факторов, называется частным коэффициентом корреляции
Частный коэффициент корреляции определяет степень зависимости между двумя переменными без учета влияния на них других факторов
Рассмотрим пример. Пусть спецификация модели имеет вид:
(3.6)
Задача. Определить корреляцию между Y и X1, исключив влияние переменной X2

ЧАСТНЫЕ КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ
Алгоритм решения заключается в следующем:
1. Строится регрессия Y на X2
2. Строится регрессия X1 на X2
3. Для удаления влияния X2 вычисляются остатки:
4. Значение частного коэффициента корреляции между переменными Y и X1 вычисляется по формуле:

ЧАСТНЫЕ КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ
Частные коэффициенты корреляции могут быть вычислены по значениям парных коэффициентов
В общем случае связь между частными и обычными коэффициентами корреляции осуществляется следующим образом:
(3.7)
(3.8)

ЧАСТНЫЕ КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ
Пример 1. Вычислить частный коэффициент корреляции r(Y,X1│X2) между переменными модели (3.6)
Пусть матрица R имеет вид:
Тогда частный коэффициент корреляции r(Y,X1│X2) вычисляется с помощью (3.7)

ЧАСТНЫЕ КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ
Пример 2. В таблице приведены данные об объеме импорта Y (млрд.дол), ВНП X1 (млрд.дол) и индексе цен X2 в США за период 1964-1979 гг
Вычислить элементы матрицы взаимных корреляций модели:
Решение.
1. Вычисляем матрицу взаимных корреляций
2. Вычисляется обратная матрица

ЧАСТНЫЕ КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ
Пример 2. (Продолжение)
3. Вычисляются оценки частных коэффициентов корреляции с помощью (3.8)
Обратная матрица R-1
Выражение (3.8)
Тогда:
Проверка гипотезы Н0: r(x1,x2│Y)=0

МЕТОДЫ УСТРАНЕНИЯ МУЛЬТИКОЛЛИНЕАРНОСТИ
Существуют следующие группы методов устранения мультиколлинеарности в уравнениях регрессии:
Методы исключения переменных модели;
Методы, которые используют внешнюю информацию;
Методы, предполагающие переход к смещенным оценкам параметров модели;
Методы преобразования данных;
Метод главных компонент

Метод дополнительных регрессий
Алгоритм метода заключается в следующем:
Строятся уравнения регрессии, которые связывают каждый из регрессоров со всеми оставшимися
2. Вычисляются коэффициенты детерминации R2 для каждого уравнения регрессии
3. Проверяется статистическая гипотеза H0: R2=0 с помощью F теста
Вывод: если гипотеза H0: R2=0 не отклоняется, значит данный регрессор не приводит к мультиколлинеарности
Основным методом устранения мультиколлинеарности заключается в исключении переменных
Существует несколько способов решения этой задачи
МЕТОДЫ УСТРАНЕНИЯ МУЛЬТИКОЛЛИНЕАРНОСТИ

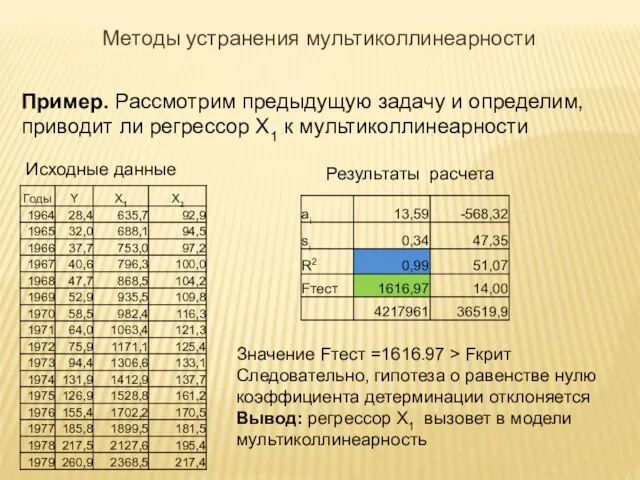
Пример. Рассмотрим предыдущую задачу и определим, приводит ли регрессор X1 к мультиколлинеарности
Исходные данные
Результаты расчета
Значение Fтест =1616.97 > Fкрит
Следовательно, гипотеза о равенстве нулю коэффициента детерминации отклоняется
Вывод: регрессор X1 вызовет в модели мультиколлинеарность
Методы устранения мультиколлинеарности

2. Метод последовательного присоединения (пошаговая регрессия)
В отличие от рассмотренного, метод последовательного присоединения регрессоров позволяет выявить набор регрессоров, который ни только не приводит к мультиколлинеарности, но и обеспечивает наилучшее качество спецификации модели
Алгоритм метода следующий:
Строится регрессионная модель с учетом всех предполагаемых регрессоров. По признакам делается вывод о возможном присутствии мультиколлинеарности
Рассчитывается матрица корреляций и выбирается регрессор, имеющий наибольшую корреляцию с эндогенной переменной
К выбранному регрессору последовательно в модель добавляется каждый из оставшихся регрессоров и вычисляются скорректированные коэффициенты детерминации для каждой из моделей.
К модели присоединяется тот регрессор, который обеспечивает наибольшее значение скорректированного R2
Методы устранения мультиколлинеарности

4. К паре выбранных регрессоров последовательно присоединяется третий из числа оставшихся Строятся модели, вычисляется скорректированный R2, добавляется тот регрессор, который обеспечивает наибольшее значение скорректированного R2
Процесс присоединения регрессоров прекращается, когда значение скорректированного R2 становится меньше достигнутого на предыдущем шаге
Замечание. Каким бы образом не осуществлялся отбор факторов, уменьшение их числа приводит к улучшению обусловленности матрицы (XTX)-1, а, следовательно, к повышению качества оценок параметров модели
Методы устранения мультиколлинеарности

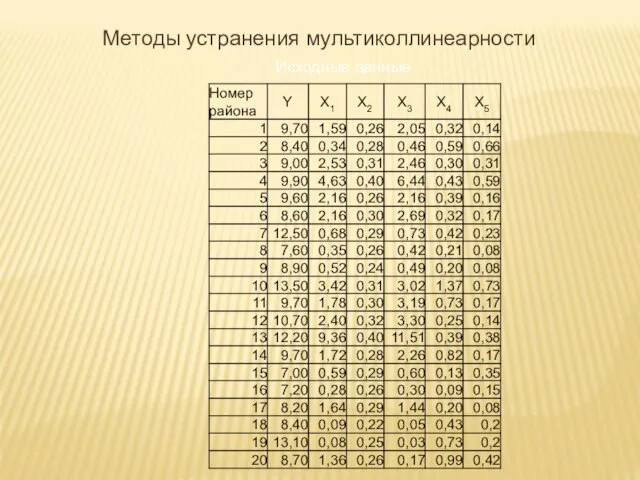
Пример 2.
Исследуется зависимость урожайности зерновых культур Y от следующих факторов производства:
X1 – число тракторов на 100га
X2 – число зерноуборочных комбайнов на 100га
X3 – Число орудий поверхностной обработки почвы на 100 га
X4 - количество удобрений, расходуемых на гектар (т/га)
X5 – количество химических средств защиты растений (т/га)
Методы устранения мультиколлинеарности

Исходные данные
Методы устранения мультиколлинеарности

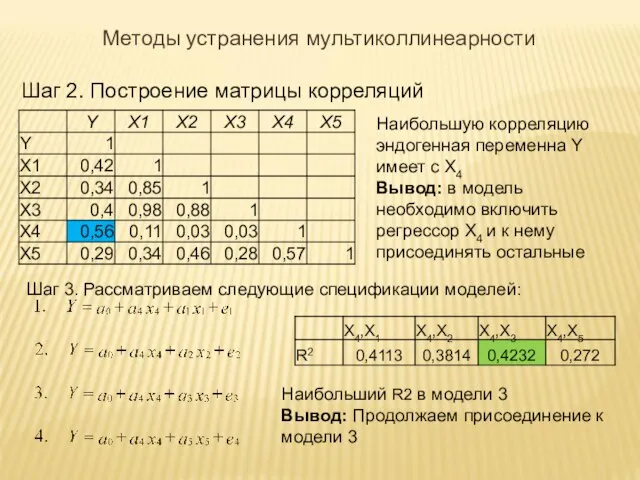
Шаг 2. Построение матрицы корреляций
Наибольшую корреляцию эндогенная переменна Y имеет с X4
Вывод: в модель необходимо включить регрессор X4 и к нему присоединять остальные
Шаг 3. Рассматриваем следующие спецификации моделей:
Наибольший R2 в модели 3
Вывод: Продолжаем присоединение к модели 3
Методы устранения мультиколлинеарности

Шаг 4. Рассматриваем следующие спецификации моделей:
Наибольший коэффициент детерминации соответствует модели 3.
Однако его значение меньше, чем было достигнуто ранее: R2=0,4232
Выводы:
1. Не имеет смысл рассматривать спецификацию 3.
2. Для построения следует принять спецификацию модели в виде:
Методы устранения мультиколлинеарности