Содержание
- 2. Приращение функции 1) Сформулируйте определения приращения аргумента и приращения функции в данной точке x0. 2) От
- 3. Физический смысл производной, рассмотрим падение тела с некоторой высоты рассмотрим промежуток Δt от момента t0 до
- 4. Определение Производной функции в точке x0 называется предел отношения приращения функции к приращению аргумента, если приращение
- 5. Определения. 1) Функция называется дифференцируемой в точке x0, если ∃f’(x0). 2) Функция называется дифференцируемой на множестве
- 6. Вычисление производных по определению 1) f(x) = C. Δf(x0) = f(x0 + Δx) – f(x0) =
- 7. Алгоритм нахождения производной: Зафиксировать значение х0 и найти f(x0) Дать аргументу х0 приращение Δ х ,и
- 8. Вычислить по определению производные 3) f(x) = ax2 + bx + c 4) f(x) = .
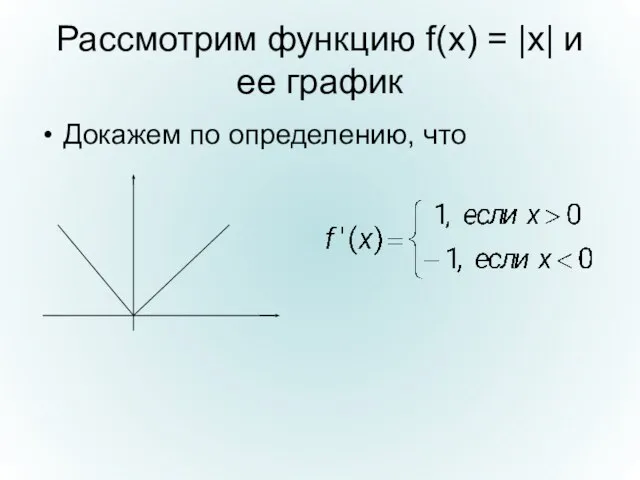
- 9. Рассмотрим функцию f(x) = |x| и ее график Докажем по определению, что
- 10. А) Пусть x0 > 0, тогда выберем Δx так, чтобы x0 + Δx > 0. Δf(x0)
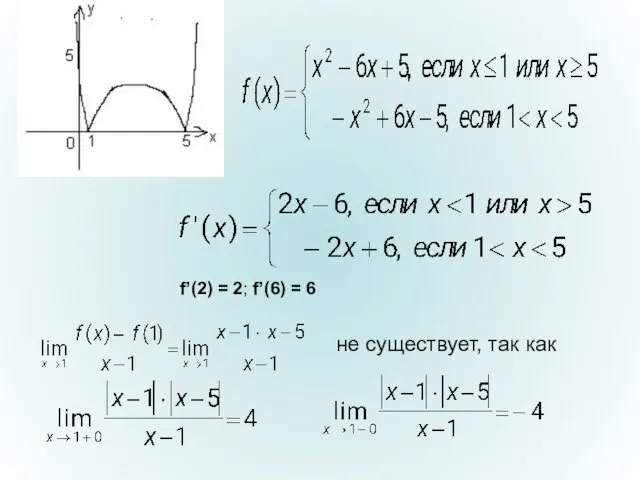
- 11. F(x) = |x2 – 6x + 5|. А) Постройте график функции. Б) Найдите f’(2) и f’(6).
- 12. f’(2) = 2; f’(6) = 6 f’(2) = 2; f’(6) = 6 не существует, так как
- 13. не существует, так как
- 15. Скачать презентацию









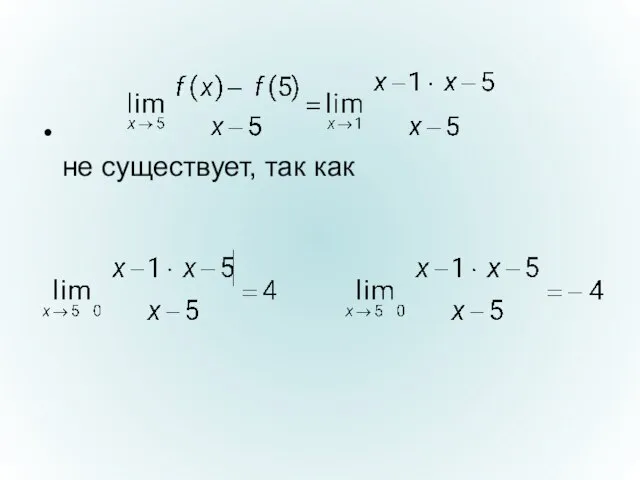
 Воскресенский дорожный колледж. Проект
Воскресенский дорожный колледж. Проект Тестовая игра Кокология
Тестовая игра Кокология Стратегический и инновационный менеджмент
Стратегический и инновационный менеджмент Реклама во Вконтакте
Реклама во Вконтакте Поле чудес на английском
Поле чудес на английском Греко-римская борьба. Тестирование технической подготовленности
Греко-римская борьба. Тестирование технической подготовленности Дыхание, его значение. Строение и функции органов дыхания
Дыхание, его значение. Строение и функции органов дыхания День открытых дверей
День открытых дверей Анализ разработки пласта Б2 Баклановского поднятия Баклановского месторождения
Анализ разработки пласта Б2 Баклановского поднятия Баклановского месторождения Одноклеточные и многоклеточные организмы
Одноклеточные и многоклеточные организмы Влияние водных ресурсов на
Влияние водных ресурсов на ФГОС: преемственность НОО и ООО
ФГОС: преемственность НОО и ООО Гениальный современник Александр Шилов
Гениальный современник Александр Шилов Ввертные петли Apecs
Ввертные петли Apecs Ранняя половая связь - половой инстинкт или распущенность?
Ранняя половая связь - половой инстинкт или распущенность? Цвет в произведениях живописи
Цвет в произведениях живописи Семь чудес света Древнего Мира
Семь чудес света Древнего Мира ритмика русский танец
ритмика русский танец Презентация на тему Исаак Бабель
Презентация на тему Исаак Бабель Приемы вычислений 1 класс Моро
Приемы вычислений 1 класс Моро ТЕМА № 2 (ХПИ)
ТЕМА № 2 (ХПИ) Татарские женские головные уборы
Татарские женские головные уборы Презентация на тему Ноев ковчег
Презентация на тему Ноев ковчег Угольная промышленность
Угольная промышленность История школьной оценки
История школьной оценки Технологический процесс приготовления сложных горячих жареных блюд из овощей
Технологический процесс приготовления сложных горячих жареных блюд из овощей проспкпЖукова
проспкпЖукова Турпоход на Перемиловскую высоту
Турпоход на Перемиловскую высоту