Содержание
- 2. Задача 1. По графику производной укажите количество промежутков возрастания непрерывной на [-7;4] функции. -7 4 Y=f'(x)
- 3. Задача 2. По графику производной, определенной на [а;b] функции, укажите длину интервала убывания функции. Y Y
- 4. Задача 3. По графику производной, определенной на [а;b] функции, укажите наименьшую точку максимума функции. Y Y
- 5. Задача 4. По графику производной, определенной на [а;b] функции, укажите количество: а)критических точек, б) точек экстремума.
- 6. Задача 5. f(x) – непрерывная на [а;b] функция. По графику ее производной определите количество: а) критических
- 7. Решите задачи 1. Найдите значение функции при наименьшем натуральном значении переменной из промежутка (промежутков) убывания функции
- 8. Проверим решение задачи 1. Производная имеет вид: f’=[(x+3)(x-5)]/(x-1)² 2. Методом интервалов находим, что производная отрицательна на
- 9. Проверим решение задачи 1. Представим производную в виде f´=(x-2)(x-1)(x+3)(x-4) 2. Решив уравнение f´(x)=0, найдем критические точки:
- 10. Решите задачи 1. Сколько корней в зависимости от параметра а имеет уравнение 2. При каком значении
- 12. Скачать презентацию
![Задача 1. По графику производной укажите количество промежутков возрастания непрерывной на [-7;4]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/369870/slide-1.jpg)
![Задача 2. По графику производной, определенной на [а;b] функции, укажите длину интервала](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/369870/slide-2.jpg)
![Задача 3. По графику производной, определенной на [а;b] функции, укажите наименьшую точку](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/369870/slide-3.jpg)
![Задача 4. По графику производной, определенной на [а;b] функции, укажите количество: а)критических](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/369870/slide-4.jpg)
![Задача 5. f(x) – непрерывная на [а;b] функция. По графику ее производной](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/369870/slide-5.jpg)

![Проверим решение задачи 1. Производная имеет вид: f’=[(x+3)(x-5)]/(x-1)² 2. Методом интервалов находим,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/369870/slide-7.jpg)


 Андреев Леонид
Андреев Леонид Коучинг в QA Дмитрий Ворончев. Acronis, Inc
Коучинг в QA Дмитрий Ворончев. Acronis, Inc МОЙСЧЕР Система глубокого увлажнения сухих волос
МОЙСЧЕР Система глубокого увлажнения сухих волос Анализ результатов деятельности школы и планирование изменений. Проблемно-ориентированный анализ.
Анализ результатов деятельности школы и планирование изменений. Проблемно-ориентированный анализ. Культурное растение лён
Культурное растение лён Социально-значимый проект "Береги себя для жизни!"
Социально-значимый проект "Береги себя для жизни!" Правила безопасного поведения при угрозе взрыва и взрыве
Правила безопасного поведения при угрозе взрыва и взрыве МЕРЛОНИ ПРОДЖЕТТИ С.П.А. 02 ноября 2011 г. г. Липецк
МЕРЛОНИ ПРОДЖЕТТИ С.П.А. 02 ноября 2011 г. г. Липецк Миф. Функция мифа
Миф. Функция мифа Анализ типичных нарушений законодательства, выявленных в ходе проверок образовательных учреждений, расположенных на территории
Анализ типичных нарушений законодательства, выявленных в ходе проверок образовательных учреждений, расположенных на территории  Найди свою книгу
Найди свою книгу Закони, які регламентують діяльність
Закони, які регламентують діяльність Презентация на тему Права ребенка
Презентация на тему Права ребенка Они гостили на Воронежской земле
Они гостили на Воронежской земле Экономическая безопасность
Экономическая безопасность Технологическое предпринимательство для школьников: от изобретения к бизнесу! Занятие 2
Технологическое предпринимательство для школьников: от изобретения к бизнесу! Занятие 2 Германия
Германия Роль социально-бытовой ориентировки в адекватной интеграции обучающихся, воспитанников школы-интерната в системе современных
Роль социально-бытовой ориентировки в адекватной интеграции обучающихся, воспитанников школы-интерната в системе современных Презентация на тему Линии пересекающиеся и непересекающиеся
Презентация на тему Линии пересекающиеся и непересекающиеся  Презентация на тему Путешествие капельки
Презентация на тему Путешествие капельки Zanyatie_1_L
Zanyatie_1_L Иванова Наталья Геннадьевна
Иванова Наталья Геннадьевна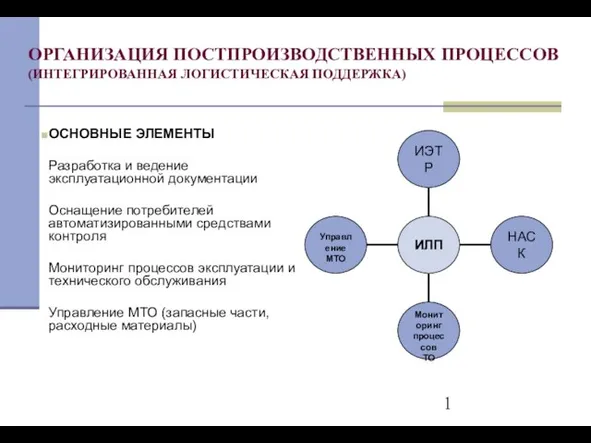 ОРГАНИЗАЦИЯ ПОСТПРОИЗВОДСТВЕННЫХ ПРОЦЕССОВ(ИНТЕГРИРОВАННАЯ ЛОГИСТИЧЕСКАЯ ПОДДЕРЖКА)
ОРГАНИЗАЦИЯ ПОСТПРОИЗВОДСТВЕННЫХ ПРОЦЕССОВ(ИНТЕГРИРОВАННАЯ ЛОГИСТИЧЕСКАЯ ПОДДЕРЖКА) Карева Е.Н.
Карева Е.Н. Интимная жизнь кожи
Интимная жизнь кожи Презентация на тему Русские народные песни
Презентация на тему Русские народные песни  ИСПОЛЬЗОВАНИЕ АФОРИЗМОВ НА УРОКАХ ФИЗИЧЕСКОЙ КУЛЬТУРЫ
ИСПОЛЬЗОВАНИЕ АФОРИЗМОВ НА УРОКАХ ФИЗИЧЕСКОЙ КУЛЬТУРЫ Роман А.А.Фадеева «Разгром»
Роман А.А.Фадеева «Разгром»