ПРОСТЫЕ МЕХАНИЗМЫ

ИСТОРИЯ ПРОСТЫХ МЕХАНИЗМОВ
С древних времен для облегчения своего труда человек использует различные механизмы (греч. "механэ" - машина, орудие).
В физике приспособления для преобразования движения и силы называют механизмами. Большинство из них были изобретены еще до Нашей эры. Например, блоки, вороты, кабестаны, полиспасты издревле применялись при кораблестроении и мореплавании.
Используемые человеком механизмы могут быть устроены очень сложно, однако для понимания их работы достаточно изучить так называемые простые механизмы - рычаг и наклонную плоскость.
В большинстве случаев простые механизмы применяют для того чтобы получить выигрыш в силе,т. е. увеличить силу действующую на тело, в несколько раз.

РАЗНОВИДНОСТИ ПРОСТЫХ МЕХАНИЗМОВ
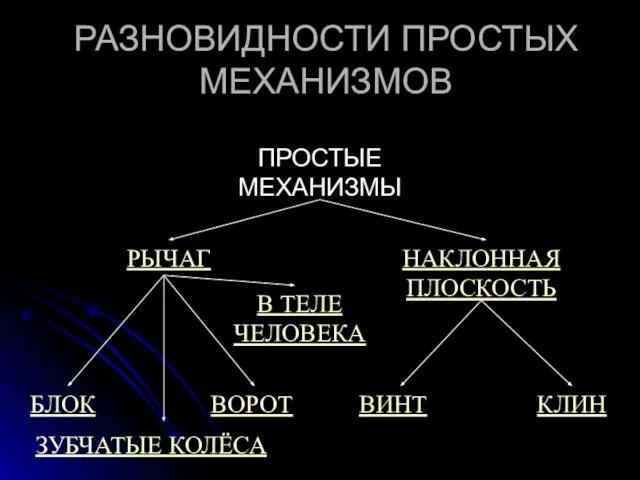
ПРОСТЫЕ МЕХАНИЗМЫ
РЫЧАГ
НАКЛОННАЯ ПЛОСКОСТЬ
БЛОК
ВОРОТ
ВИНТ
КЛИН
ЗУБЧАТЫЕ КОЛЁСА
В ТЕЛЕ ЧЕЛОВЕКА

РЫЧАГ
Рычаг - это жесткий стержень, который может свободно поворачиваться относительно неподвижной точки, называемой точкой опоры. Примером рычага могут служить лом, молоток с расщепом, тачка, метла.
Рычаги бывают трех родов, различающихся взаимным расположением точек приложения нагрузки и усилия и точки опоры.

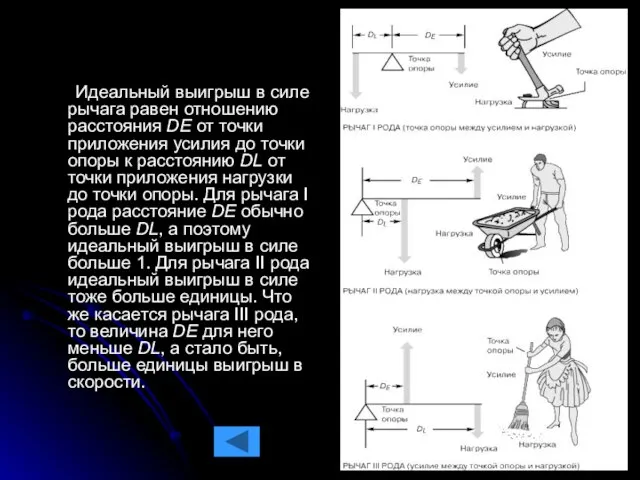
Идеальный выигрыш в силе рычага равен отношению расстояния DE от точки приложения усилия до точки опоры к расстоянию DL от точки приложения нагрузки до точки опоры. Для рычага I рода расстояние DE обычно больше DL, а поэтому идеальный выигрыш в силе больше 1. Для рычага II рода идеальный выигрыш в силе тоже больше единицы. Что же касается рычага III рода, то величина DE для него меньше DL, а стало быть, больше единицы выигрыш в скорости.

БЛОК
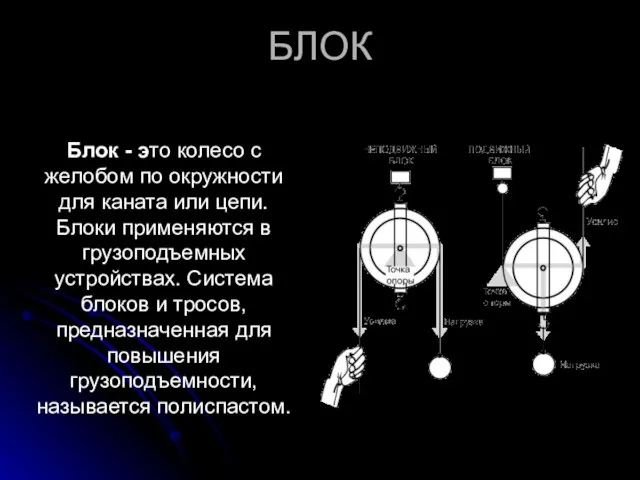
Блок - это колесо с желобом по окружности для каната или цепи. Блоки применяются в грузоподъемных устройствах. Система блоков и тросов, предназначенная для повышения грузоподъемности, называется полиспастом.

Одиночный блок может быть либо с закрепленной осью (уравнительным), либо подвижным. Блок с закрепленной осью действует как рычаг I рода с точкой опоры на его оси. Поскольку плечо усилия равно плечу нагрузки (радиус блока), идеальный выигрыш в силе и скорости равен 1. Подвижный же блок действует как рычаг II рода, поскольку нагрузка расположена между точкой опоры и усилием. Плечо нагрузки (радиус блока) вдвое меньше плеча усилия (диаметр блока). Поэтому для подвижного блока идеальный выигрыш в силе равен 2.

ВОРОТ
Это, в сущности, два колеса, соединенные вместе и вращающиеся вокруг одной оси, например, колодезный ворот с ручкой.
Ворот может давать выигрыш как в силе, так и в скорости. Это зависит от того, где прилагается усилие, а где – нагрузка, поскольку он действует как рычаг I рода. Точка опоры расположена на закрепленной (фиксированной) оси, а поэтому плечи усилия и нагрузки равны радиусам соответствующих колес. Пример такого устройства для выигрыша в силе – отвертка, а для выигрыша в скорости – шлифовальный круг.

ЗУБЧАТЫЕ КОЛЁСА
Система двух находящихся в зацеплении зубчатых колес, сидящих на валах одинакового диаметра, в какой-то мере аналогична дифференциальному вороту. Скорость вращения колес обратно пропорциональна их диаметру. Если малая ведущая шестерня A (к которой приложено усилие) по диаметру вдвое меньше большого зубчатого колеса B, то она должна вращаться вдвое быстрее. Таким образом, выигрыш в силе такой зубчатой передачи равен 2. Но если точки приложения усилия и нагрузки поменять местами, так что колесо B станет ведущим, то выигрыш в силе будет равен 1/2, а выигрыш в скорости – 2.

НАКЛОННАЯ ПЛОСКОСТЬ
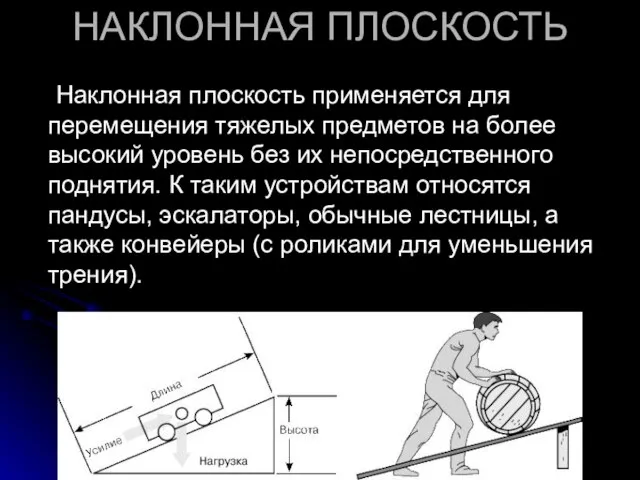
Наклонная плоскость применяется для перемещения тяжелых предметов на более высокий уровень без их непосредственного поднятия. К таким устройствам относятся пандусы, эскалаторы, обычные лестницы, а также конвейеры (с роликами для уменьшения трения).

Идеальный выигрыш в силе, обеспечиваемый наклонной плоскостью, равен отношению расстояния, на которое перемещается нагрузка, к расстоянию, проходимому точкой приложения усилия. Первое есть длина наклонной плоскости, а второе – высота, на которую поднимается груз. Поскольку гипотенуза больше катета, наклонная плоскость всегда дает выигрыш в силе. Выигрыш тем больше, чем меньше наклон плоскости. Этим объясняется то, что горные автомобильные и железные дороги имеют вид серпантина: чем меньше крутизна дороги, тем легче по ней подниматься.

КЛИН
Это, в сущности, сдвоенная наклонная плоскость. Главное его отличие от наклонной плоскости в том, что она обычно неподвижна, и груз под действием усилия движется по ней, а клин вгоняют под нагрузку или в нагрузку. Принцип клина используется в таких инструментах и орудиях, как топор, зубило, нож, гвоздь, швейная игла.
Идеальный выигрыш в силе, даваемый клином, равен отношению его длины к толщине на тупом конце. Реальный выигрыш клина, в отличие от других простейших механизмов, трудно определить. Сопротивление, встречаемое им, непредсказуемо меняется для разных участков его «щек».

ВИНТ
Резьба винта – это, в сущности, наклонная плоскость, многократно обернутая вокруг цилиндра. В зависимости от направления подъема наклонной плоскости винтовая резьба может быть левой (A) или правой (B). Сопрягающаяся деталь, естественно, должна иметь резьбу такого же направления. Примеры простых устройств с винтовой резьбой – домкрат, болт с гайкой, микрометр, тиски.

Поскольку резьба – наклонная плоскость, она всегда дает выигрыш в силе. Идеальный выигрыш равен отношению расстояния, проходимого точкой приложения усилия за один оборот винта (длины окружности), к расстоянию, проходимому при этом нагрузкой по оси винта. За один оборот нагрузка перемещается на расстояние между двумя соседними витками резьбы (a и b или b и c на рисунке), которое называется шагом резьбы. Шаг резьбы обычно значительно меньше ее диаметра, так как иначе слишком велико трение.

БИОМЕХАНИКА
БИОМЕХАНИКА (от греч. bios — жизнь и механика), изучает механические свойства живых тканей, органов и организма в целом, а также происхождение в них механического явления (при движениях, дыхании).
Биомеханика рассматривает органы в теле человека как механизмы.