Содержание
- 2. План лекции
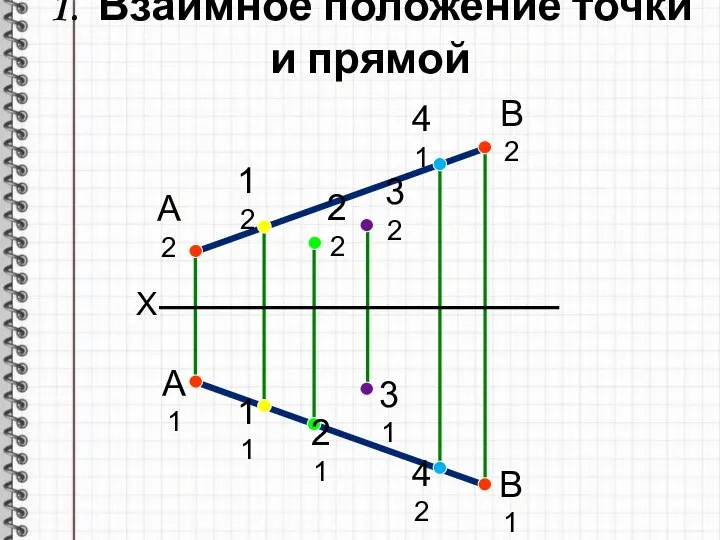
- 3. 1. Взаимное положение точки и прямой X А2 В2 А1 В1 12 11 22 21 32
- 4. Если точка принадлежит прямой, то проекции точки принадлежат одноименным проекциям прямой 1. Взаимное положение точки и
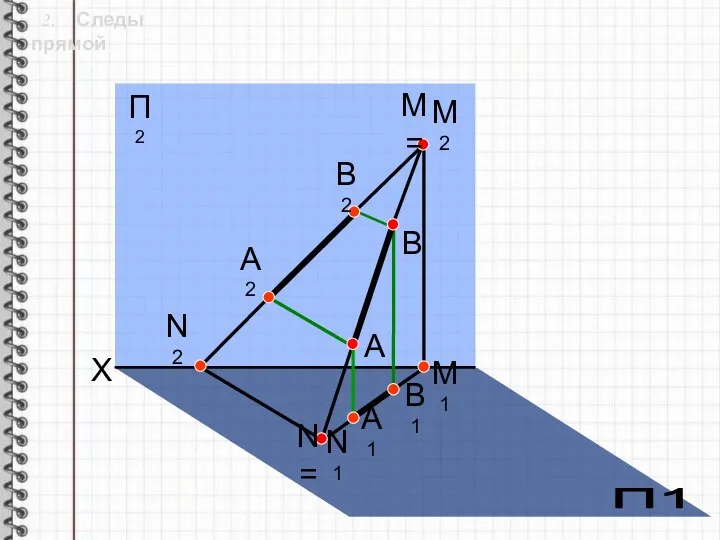
- 5. 2. Следы прямой Определение: След прямой - точка пересечения прямой с плоскостью проекций.
- 6. 2. Следы прямой X А1 В А В1 А2 В2 N= N1 N2 M2 M= M1
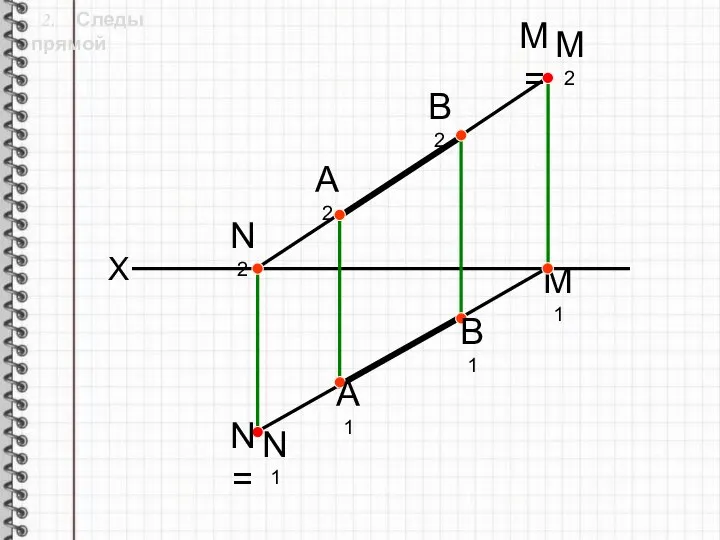
- 7. 2. Следы прямой А1 В1 А2 N= N1 N2 M2 M1 B2 X M=
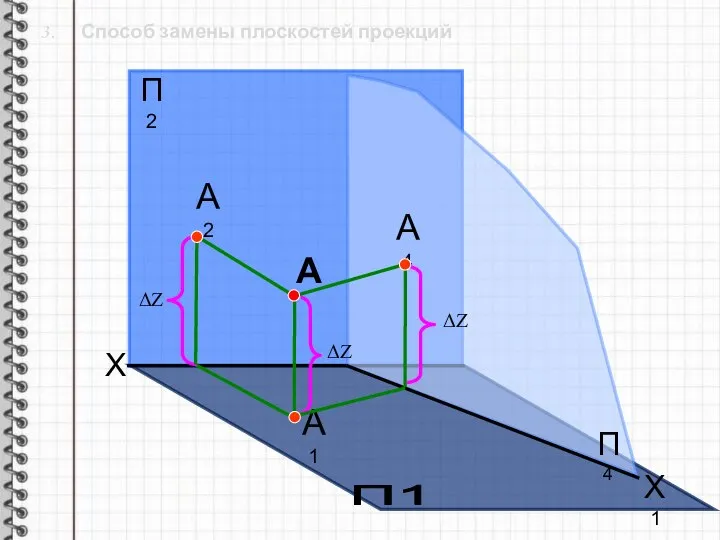
- 8. 3. Способ замены плоскостей проекций Способ замены плоскостей проекций заключается в последовательной замене одной из плоскостей
- 9. 3. Способ замены плоскостей проекций При этом должны быть выдержаны следующие условия: 1. Новая плоскость должна
- 10. 3. Способ замены плоскостей проекций X П2 П1 А1 А А2 П4 Х1 А4 ΔΖ ΔΖ
- 11. 3. Способ замены плоскостей проекций X П2 П1 П4 Х1
- 12. 3. Способ замены плоскостей проекций X П2 П1 Х1 П4
- 13. 3. Способ замены плоскостей проекций X П2 П1 Х1 П4
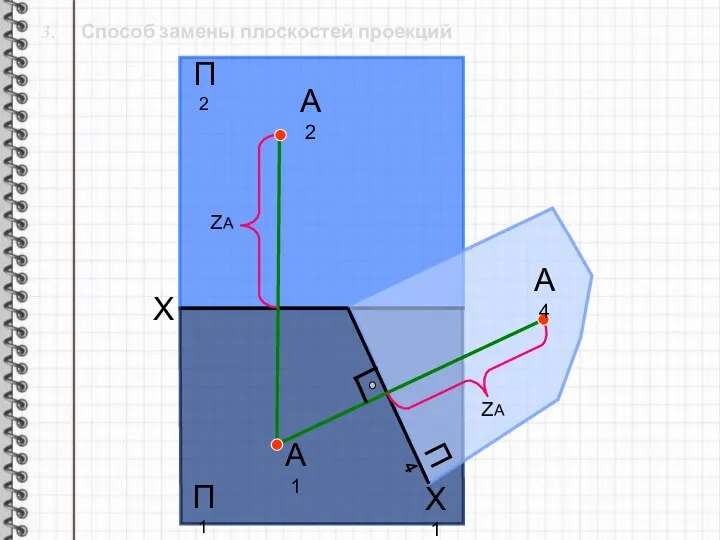
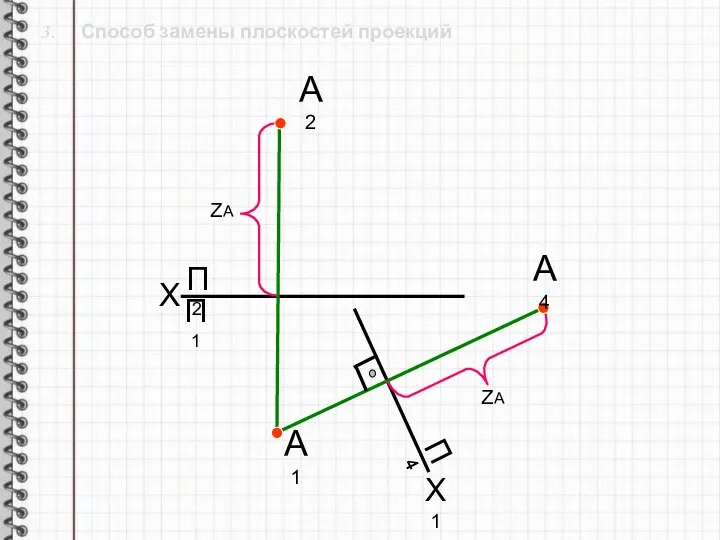
- 14. 3. Способ замены плоскостей проекций X П2 Х1 П1 П4 А1 А2 ZА ZА А4
- 15. 3. Способ замены плоскостей проекций X П2 Х1 П1 П4 А1 А2 ZА ZА А4
- 16. 4. Преобразование чертежа прямой Прямая общего положения может быть преобразована в: 1. Прямую уровня 2. Проецирующую
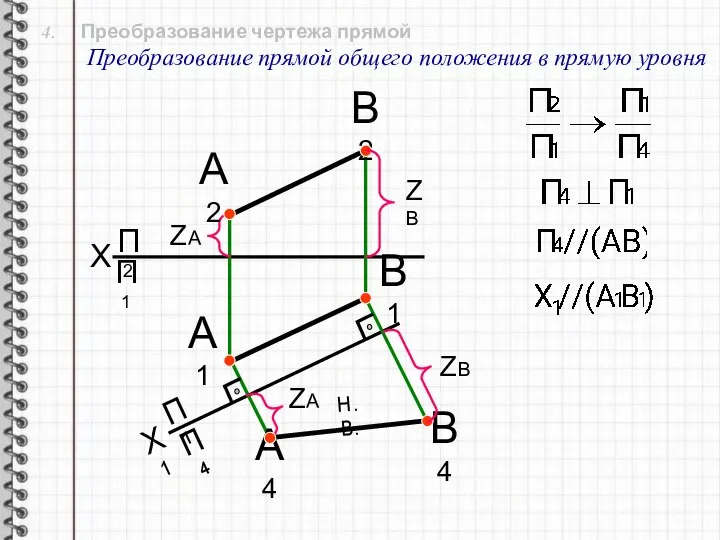
- 17. 4. Преобразование чертежа прямой Преобразование прямой общего положения в прямую уровня X П2 Х1 П1 П4
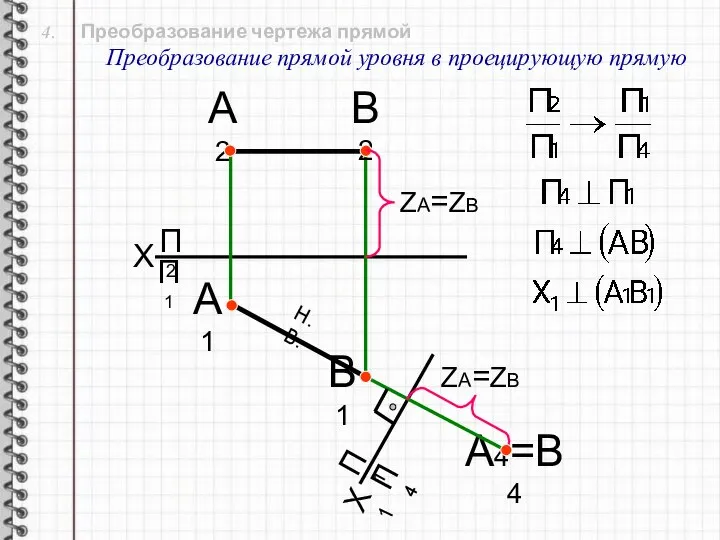
- 18. 4. Преобразование чертежа прямой Преобразование прямой уровня в проецирующую прямую X П2 Х1 П1 П4 А1
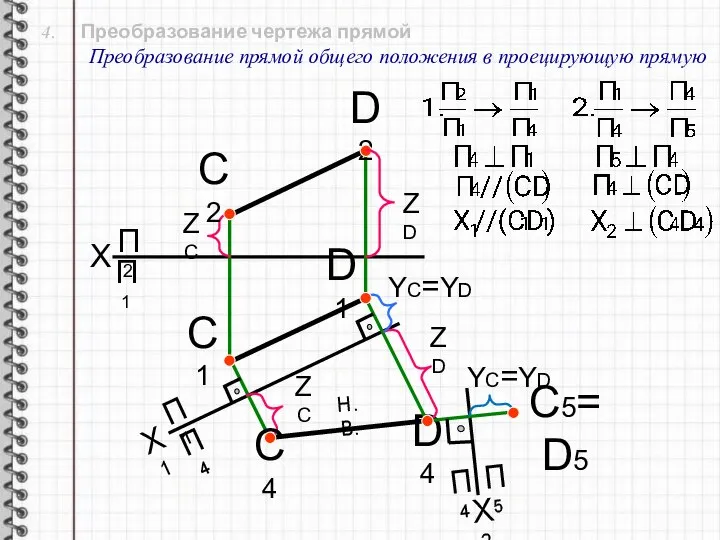
- 19. 4. Преобразование чертежа прямой Преобразование прямой общего положения в проецирующую прямую X П2 Х1 П1 П4
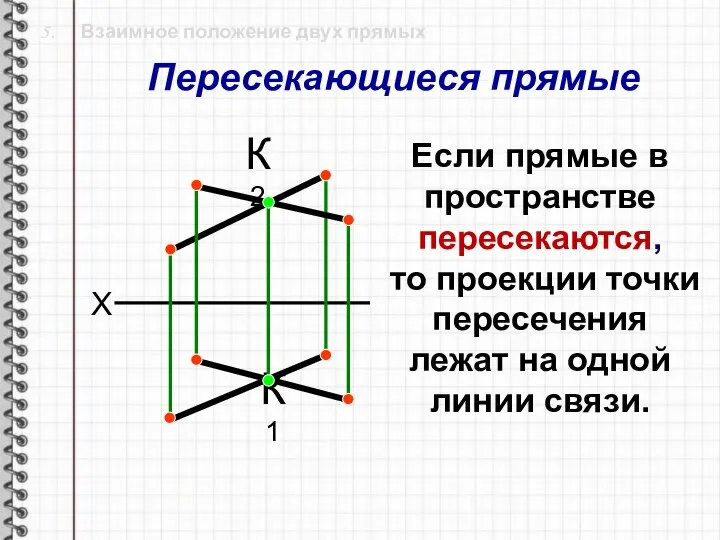
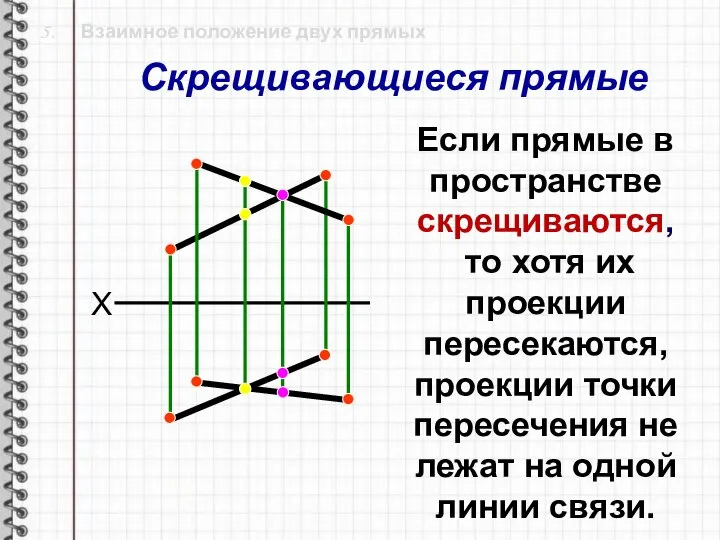
- 20. 5. Взаимное положение двух прямых Прямые в пространстве могут быть: пересекающимися; скрещивающимися; параллельными (в частности совпадать).
- 21. 5. Взаимное положение двух прямых К1 К2 X Если прямые в пространстве пересекаются, то проекции точки
- 22. 5. Взаимное положение двух прямых X Если прямые в пространстве скрещиваются, то хотя их проекции пересекаются,
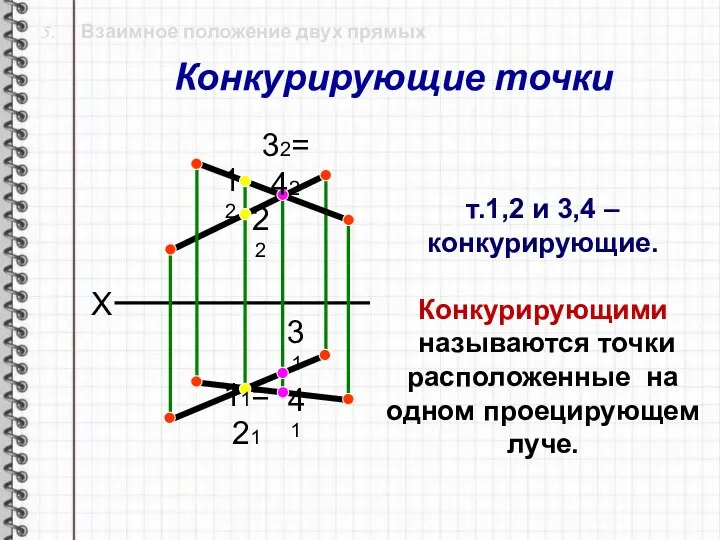
- 23. 5. Взаимное положение двух прямых X т.1,2 и 3,4 – конкурирующие. Конкурирующими называются точки расположенные на
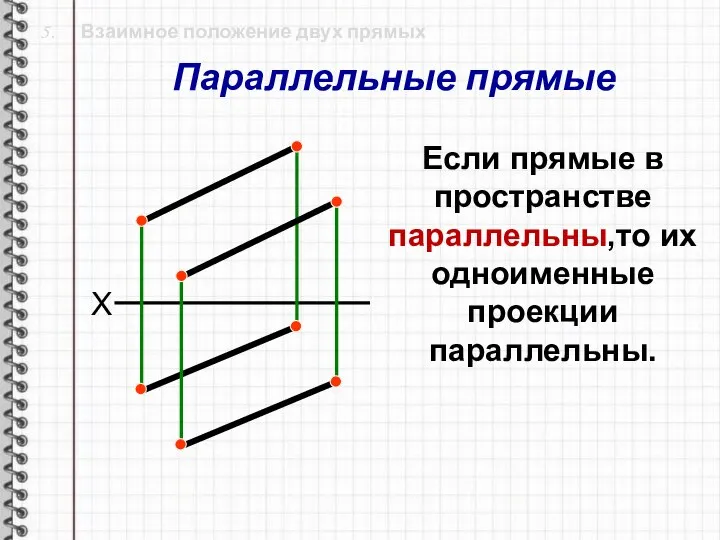
- 24. 5. Взаимное положение двух прямых X Если прямые в пространстве параллельны,то их одноименные проекции параллельны. Параллельные
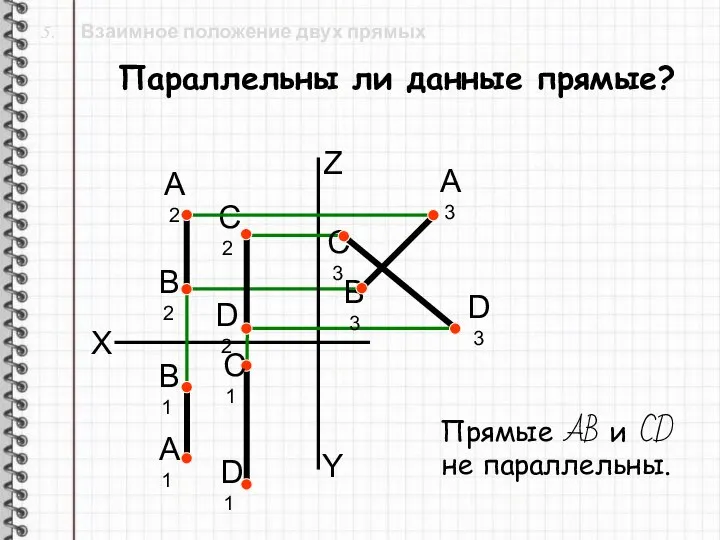
- 25. 5. Взаимное положение двух прямых X Параллельны ли данные прямые? Z Y B1 B2 A1 D1
- 26. 6. Проекции плоских углов В зависимости от положения сторон плоского угла по отношению к плоскости проекций
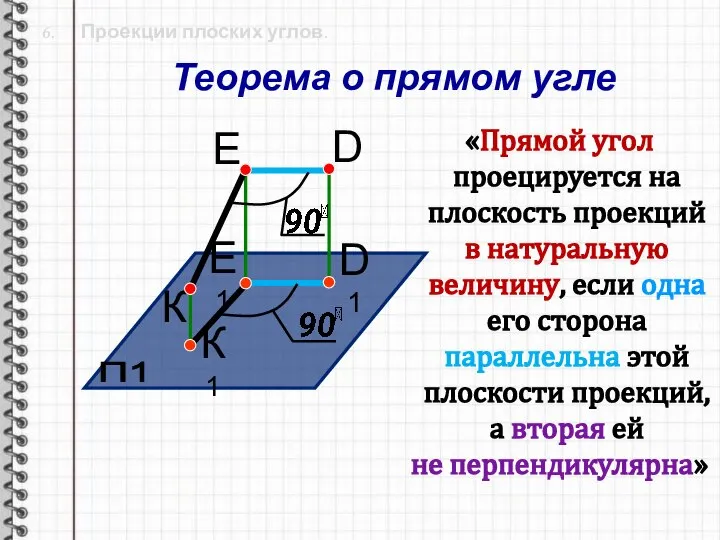
- 27. 6. Проекции плоских углов. «Прямой угол проецируется на плоскость проекций в натуральную величину, если одна его
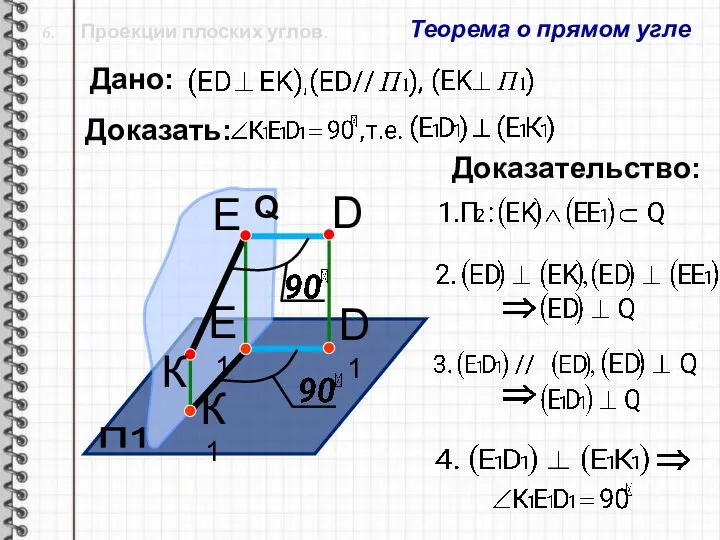
- 28. 6. Проекции плоских углов. Теорема о прямом угле П1 D1 D К1 Дано: Доказать: Доказательство: Q
- 30. Скачать презентацию








 Колледж железнодорожной медицины
Колледж железнодорожной медицины Волож Аркадий Юрьевич Генеральный директор Соколов Алексей Юрьевич Директор по развитию сетевой инфраструктуры
Волож Аркадий Юрьевич Генеральный директор Соколов Алексей Юрьевич Директор по развитию сетевой инфраструктуры Небеса коснулись меня Я тону в присутствии Вижу на престоле Царя Он в меня поверил Чем могу воздать Тебе мой Бог
Небеса коснулись меня Я тону в присутствии Вижу на престоле Царя Он в меня поверил Чем могу воздать Тебе мой Бог «Личностно - ориентированное взаимодействие педагога и ребёнка на уроках коми языка и литературы»
«Личностно - ориентированное взаимодействие педагога и ребёнка на уроках коми языка и литературы» А.А.СапроновВице-президентОАО «НК «Роснефть»
А.А.СапроновВице-президентОАО «НК «Роснефть» Естественные системы человека для защиты от негативных воздействий
Естественные системы человека для защиты от негативных воздействий Мир Леонардо да Винчи15апреля1452г. – 2мая 1519г.
Мир Леонардо да Винчи15апреля1452г. – 2мая 1519г. Я люблю тебя, Татарстан
Я люблю тебя, Татарстан  Приготовление супов-пюре
Приготовление супов-пюре Торговый кодекс 1807 г. Развитие французского гражданского и торгового права в XIX – XX вв
Торговый кодекс 1807 г. Развитие французского гражданского и торгового права в XIX – XX вв Презентация на тему Приспособленность организмов к среде обитания
Презентация на тему Приспособленность организмов к среде обитания Подготовка кадров для рыночной электроэнергетикиК вопросу развития системы управления процессами государственного тарифного р
Подготовка кадров для рыночной электроэнергетикиК вопросу развития системы управления процессами государственного тарифного р Кафедра общей гигиены СамГМУ
Кафедра общей гигиены СамГМУ Презентация на тему Интерактивная доска
Презентация на тему Интерактивная доска Презентация на тему Жизнь и творчество Н.А. Заболоцкого
Презентация на тему Жизнь и творчество Н.А. Заболоцкого  К В Н по русскому языку
К В Н по русскому языку Дебюрократизация возвращение свободы
Дебюрократизация возвращение свободы Политические режимы
Политические режимы Острый и хронический ларингит. Отек и стеноз гортани
Острый и хронический ларингит. Отек и стеноз гортани  Дистанционные методы обучения
Дистанционные методы обучения 20141104_2_osobo_okhranyaemye_prirodnye_territorii_u._o
20141104_2_osobo_okhranyaemye_prirodnye_territorii_u._o Распределение солнечного тепла и света на Земле
Распределение солнечного тепла и света на Земле Решение показательных уравнений 10 класс
Решение показательных уравнений 10 класс Что такое сила трения, и что случится, если ее отменить?
Что такое сила трения, и что случится, если ее отменить? Создание документов в текстовых редакторах
Создание документов в текстовых редакторах Размножение на клеточном и организменном уровне
Размножение на клеточном и организменном уровне Панки
Панки Урок розвитку зв'язного мовлення.
Урок розвитку зв'язного мовлення.