Содержание
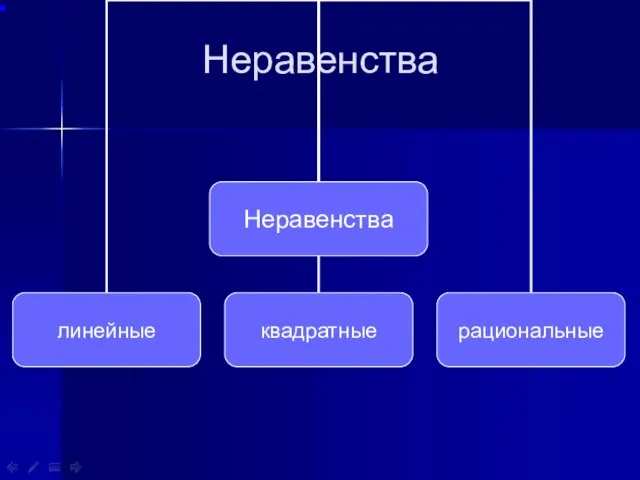
- 2. Неравенства
- 3. Линейные неравенства Линейным неравенством с одной переменной х называется неравенство вида ах + b › 0,
- 4. Пример 1: Являются ли числа 3, -5 решением данного неравенства 4х + 5 При х =
- 5. Два неравенства f(х) Правила (преобразования неравенств, приводящие к равносильным неравенствам): 1. Любой член неравенства можно перенести
- 6. 2: а) обе части неравенства можно умножить или разделить на одно и то же положительное число,
- 7. 3.а) Обе части неравенства можно умножить или разделить на одно и то же отрицательное число, изменив
- 8. Решите неравенство: 5х + 3(2х – 1)>13х - 1 Решение: 5х + 6х – 3 >13х
- 9. Квадратные неравенства Неравенства вида ах2 + bх + с > 0, где а ≠ 0, а,b,с
- 10. Алгоритм применения графического метода: 1. Найти корни квадратного трехчлена ах2+bх+с, т.е. решить уравнение ах2+bх+с=0. 2.Отметить найденные
- 11. Решите неравенство: 3х + 9 Ответ: х 3 или (-∞;-1,5)U(3;+∞).
- 12. Алгоритм выполнения метода интервалов: 1. Разложить на множители квадратный трехчлен, используя формулу ах2+bх+с = а(х-х1)(х-х2), где
- 13. Решите неравенство: х2 – 6х + 8 > 0 Решение: Разложим квадратный трехчлен х2 – 6х
- 15. Скачать презентацию











 Защита
Защита Вредные привычки.
Вредные привычки. МОНИТОРИНГ И ОЦЕНКА РАДОНОВОЙ ОПАСНОСТИ
МОНИТОРИНГ И ОЦЕНКА РАДОНОВОЙ ОПАСНОСТИ Клеточная оболочка и цитоплазма
Клеточная оболочка и цитоплазма Госзакупки. Электронные торги. Как работать на электронных торговых площадках(Семинар 01.06.2011)
Госзакупки. Электронные торги. Как работать на электронных торговых площадках(Семинар 01.06.2011) Иванова Нина Борисовна учитель биологии МБОУ «Себежская средняя общеобразователь- ная школа» г.Себеж
Иванова Нина Борисовна учитель биологии МБОУ «Себежская средняя общеобразователь- ная школа» г.Себеж 24.09pptx
24.09pptx Практика взаимодействия с заинтересованными сторонами при подготовке отчетов в области устойчивого развития
Практика взаимодействия с заинтересованными сторонами при подготовке отчетов в области устойчивого развития Педагогический состав МО начальных классов
Педагогический состав МО начальных классов Пластиковая карта Банка Казани
Пластиковая карта Банка Казани Фотоэффект
Фотоэффект Услуги по выплате единовременного пособия беременной жене военнослужащего,
Услуги по выплате единовременного пособия беременной жене военнослужащего, Черная металлургия
Черная металлургия Презентация на тему Физиология эндокринных желез
Презентация на тему Физиология эндокринных желез  Организация международного маркетинга
Организация международного маркетинга  Раскряжевка древесины
Раскряжевка древесины Производственная сигнализация при выполнении такелажных работ
Производственная сигнализация при выполнении такелажных работ Республика Азербайджан
Республика Азербайджан Внедрение биометрических документов в Республике Беларусь
Внедрение биометрических документов в Республике Беларусь 9 класс История 19.09.2022
9 класс История 19.09.2022 Региональный ресурсный центр лидерства и компетенций. Формирование цели у человека
Региональный ресурсный центр лидерства и компетенций. Формирование цели у человека Преобразование рисунка
Преобразование рисунка \виды страховок: групповая, самостраховка, комбинированная. Приемы и способы страховки. Выбор места страховки
\виды страховок: групповая, самостраховка, комбинированная. Приемы и способы страховки. Выбор места страховки Основы эпидемиологии
Основы эпидемиологии Моделирование и управление электроэнергетическими системами. Шаблон
Моделирование и управление электроэнергетическими системами. Шаблон Диаграммы потоков данных
Диаграммы потоков данных Правовые основы декларирования товаров
Правовые основы декларирования товаров Семейные традиции семьи Сухановских
Семейные традиции семьи Сухановских