Содержание
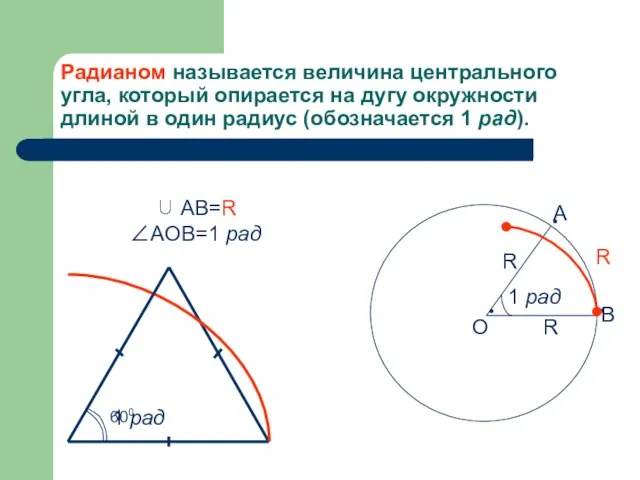
- 2. Радианом называется величина центрального угла, который опирается на дугу окружности длиной в один радиус (обозначается 1
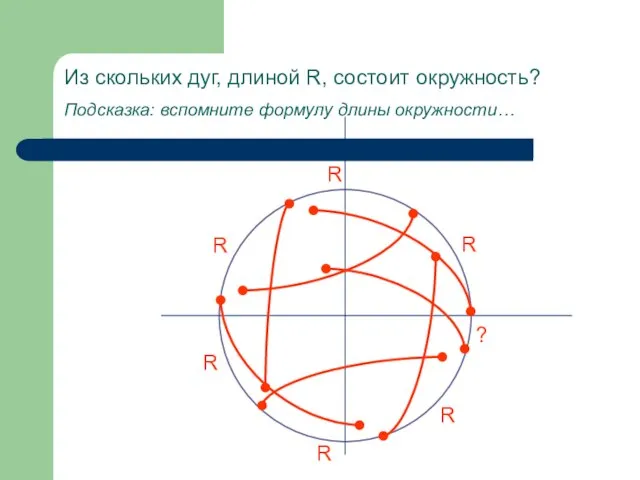
- 3. Из скольких дуг, длиной R, состоит окружность? Подсказка: вспомните формулу длины окружности… R R R R
- 4. Задание 1. Вывести правила перевода из радианной меры в градусную и наоборот. Ответ: α0= α0· рад
- 5. Окружность с центром в начале системы координат Oxy и радиусом, равным единице, называется единичной, а ограниченный
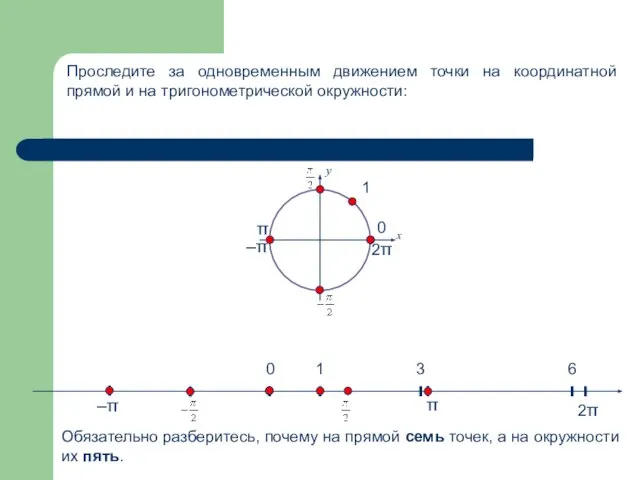
- 6. 0 1 0 3 2π 6 π π 2π у х 1 –π –π Проследите за
- 7. Так как дуги – это части окружности, то длины некоторых из них будут выражены через число
- 8. Напомним, что декартова система разбивается координатными осями на четыре координатные четверти – I, II, III и
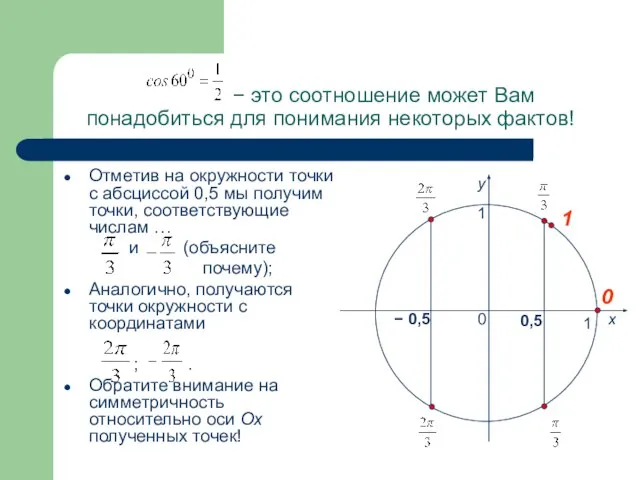
- 9. − это соотношение может Вам понадобиться для понимания некоторых фактов! Отметив на окружности точки с абсциссой
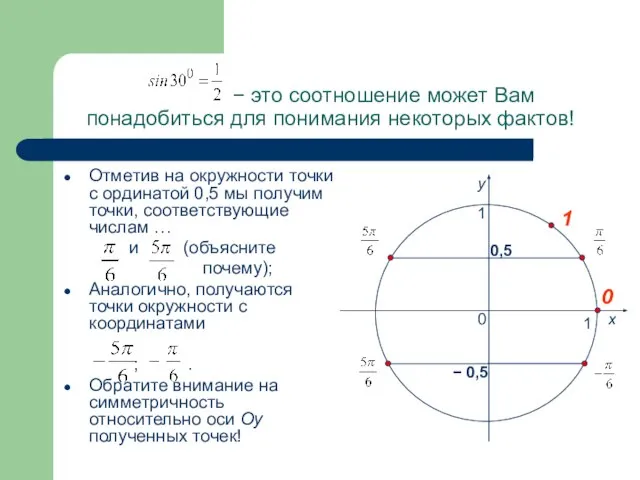
- 10. − это соотношение может Вам понадобиться для понимания некоторых фактов! Отметив на окружности точки с ординатой
- 12. Скачать презентацию




 Сохраняя традиции вкуса, используя уникальные современные технологии, мы создали для Вас столовые приборы, которые сделают Вашу ж
Сохраняя традиции вкуса, используя уникальные современные технологии, мы создали для Вас столовые приборы, которые сделают Вашу ж Технология возведения подземных инженерных сооружений
Технология возведения подземных инженерных сооружений Жан Пиаже
Жан Пиаже Презентация на тему Разработка экспортных и импортных контрактов
Презентация на тему Разработка экспортных и импортных контрактов  ИССЛЕДОВАНИЕ РОЛИ ЭКСПЕРТНОГО СООБЩЕСТВА, СМИ, ОТРАСЛЕВЫХ АССОЦИАЦИЙ, ДРУГИХ ОБЩЕСТВЕННЫХ ОБЪЕДИНЕНИЙ В ОПРЕДЕЛЕНИИ ПРОДОВОЛЬСТ
ИССЛЕДОВАНИЕ РОЛИ ЭКСПЕРТНОГО СООБЩЕСТВА, СМИ, ОТРАСЛЕВЫХ АССОЦИАЦИЙ, ДРУГИХ ОБЩЕСТВЕННЫХ ОБЪЕДИНЕНИЙ В ОПРЕДЕЛЕНИИ ПРОДОВОЛЬСТ PowerPoint Show by Andrew
PowerPoint Show by Andrew СООО ПП Полесье - крупнейший производитель пластмассовых игрушек
СООО ПП Полесье - крупнейший производитель пластмассовых игрушек Портфолио успешной личности (9 КЛАСС)
Портфолио успешной личности (9 КЛАСС) Деятельность ОУ в реализации проекта «Профилактика правонарушений среди несовершеннолетних»
Деятельность ОУ в реализации проекта «Профилактика правонарушений среди несовершеннолетних» Библиотека университета Барселоны
Библиотека университета Барселоны Читаем классику без словаря
Читаем классику без словаря Аттракцион колотушка: маленькое яблоко
Аттракцион колотушка: маленькое яблоко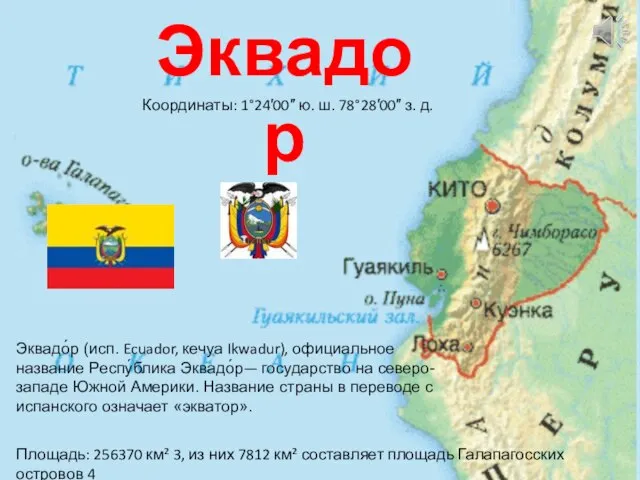 Презентация на тему Эквадор
Презентация на тему Эквадор Рекламная кампания центра дополнительного образования
Рекламная кампания центра дополнительного образования Решение задач на построение сечений..pptx
Решение задач на построение сечений..pptx Образовательная система «ГРАНИ БОГАТСТВА» Чтобы заработать на жизнь, надо работать, но чтобы разбогатеть нужно представить что-то
Образовательная система «ГРАНИ БОГАТСТВА» Чтобы заработать на жизнь, надо работать, но чтобы разбогатеть нужно представить что-то Общественное здоровье
Общественное здоровье Мировой океан проблемы
Мировой океан проблемы Презентация на тему Типы собеседников
Презентация на тему Типы собеседников ПРИСТАВКИ
ПРИСТАВКИ Алканы
Алканы Коррупция как препятствие развития предпринимательской деятельности в регионе
Коррупция как препятствие развития предпринимательской деятельности в регионе Эвакуация населения
Эвакуация населения Внедрение нового формата ведения бизнеса
Внедрение нового формата ведения бизнеса Система работы по выполнению ФЗ № 120 «Об основах системы профилактики правонарушений и безнадзорности несовершеннолетних» в МОУ
Система работы по выполнению ФЗ № 120 «Об основах системы профилактики правонарушений и безнадзорности несовершеннолетних» в МОУ  Пушкин и Тамбовский край
Пушкин и Тамбовский край Подготовка к сочинению в форме эссе "Человек и война" 11 класс
Подготовка к сочинению в форме эссе "Человек и война" 11 класс Публикация материалов в сборнике проектных технологий
Публикация материалов в сборнике проектных технологий