Содержание
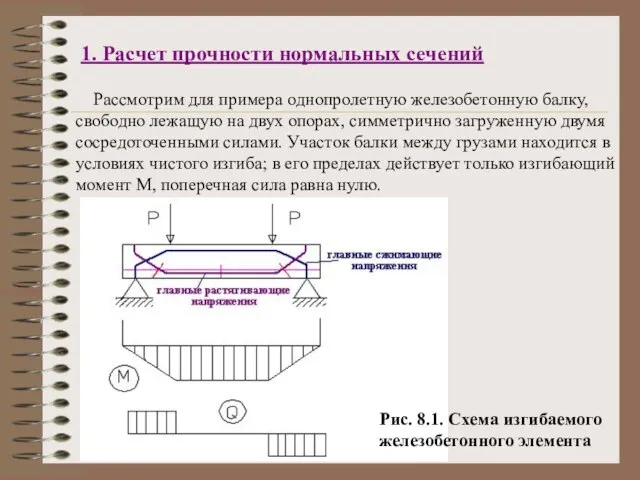
- 2. 1. Расчет прочности нормальных сечений Рассмотрим для примера однопролетную железобетонную балку, свободно лежащую на двух опорах,
- 3. В сечениях, нормальных к продольной оси элементов – изгибаемых, внецентренно сжатых, внецентренно растянутых – при двузначной
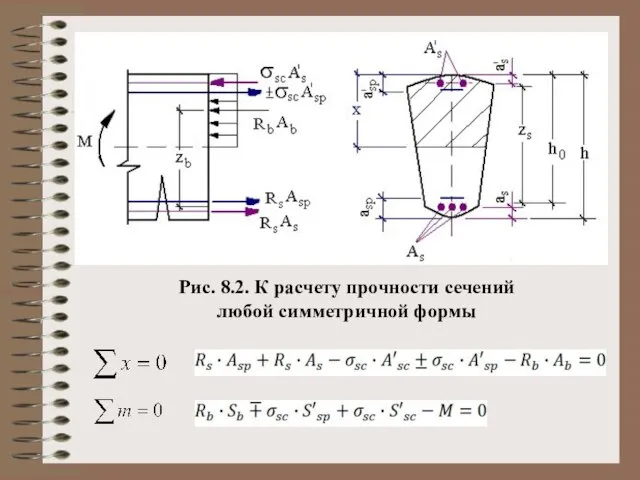
- 4. Рис. 8.2. К расчету прочности сечений любой симметричной формы
- 5. 2. Общий случай расчета нормальных сечений Основные предпосылки: 1. растянутый бетон в деформировании сечения не учитывается;
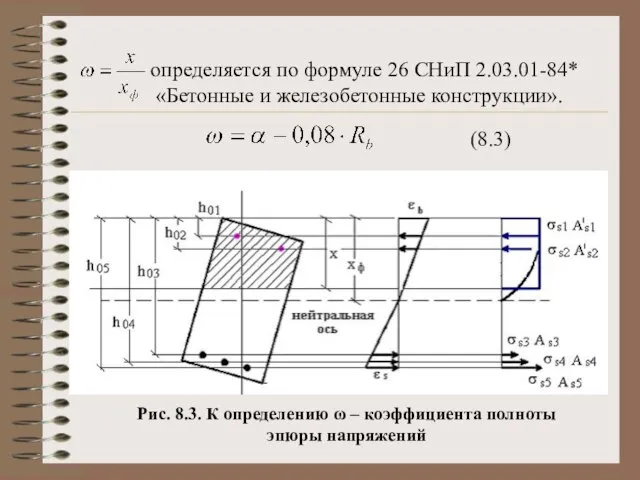
- 6. – определяется по формуле 26 СНиП 2.03.01-84* «Бетонные и железобетонные конструкции». (8.3) Рис. 8.3. К определению
- 7. Высоту сжатой зоны для сечений, деформирующихся по случаю 1, когда в растянутой арматуре и сжатом бетоне
- 8. Распределение напряжений по высоте сечений происходит линейно: (8.6)
- 9. предельная деформация в бетоне сжатой зоны (8.7) где предельная деформация в арматуре сжатой зоны. При центральном
- 10. Тогда (8.8) напряжение в i-ом стержне продольной арматуры: (8.9) где предельное напряжение в арматуре сжатой зоны;
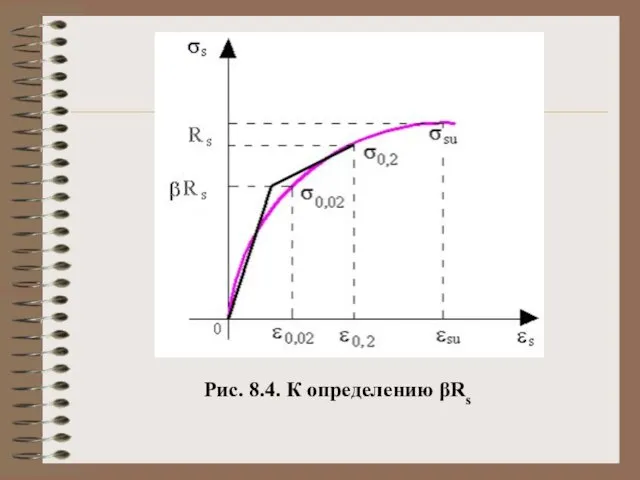
- 11. Рис. 8.4. К определению βRs
- 14. При механическом, а также автоматизированных электротермическом, электромеханическом способах предварительного напряжения арматуры классов A-IV (A600), A-V (A800),
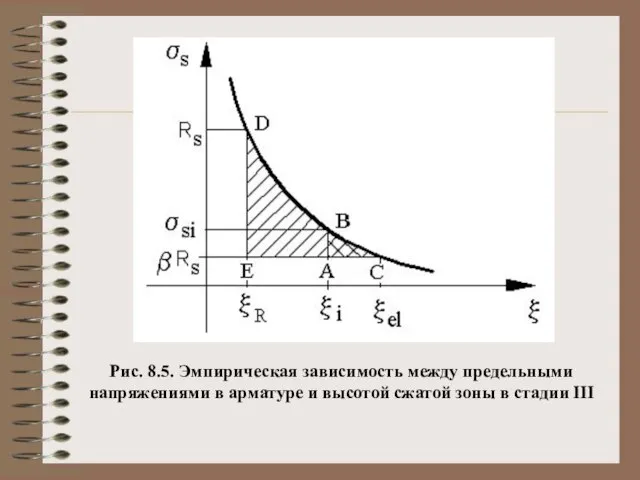
- 15. Рис. 8.5. Эмпирическая зависимость между предельными напряжениями в арматуре и высотой сжатой зоны в стадии III
- 16. Из подобия треугольников ABC ~ EDC: (8.12) (8.13) (8.14)
- 17. Определение граничной высоты сжатой зоны Принимаем предположение, что . Тогда и уравнение (8.9) преобразуется: (8.15) или
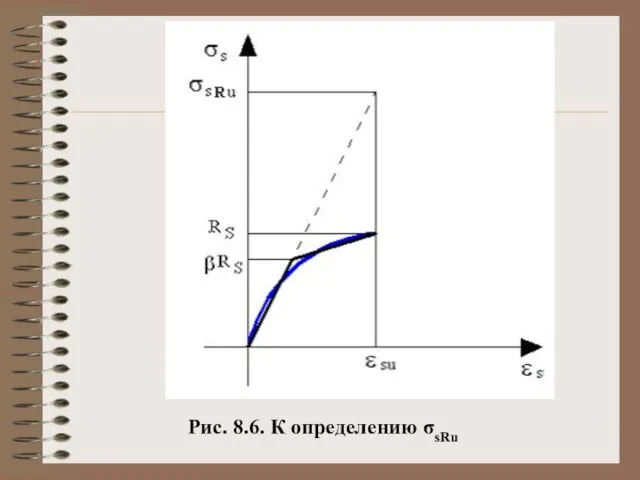
- 18. (8.16) (8.17) условное напряжение, которое при выполнении закона Гука соответствует граничной высоте сжатой зоны.
- 19. Рис. 8.6. К определению σsRu
- 20. напряжение в арматуре, МПа, принимаемое для арматуры классов: A-I (А240), A-II (А300), A-III (А400), Bp-I (Вр500)
- 22. Скачать презентацию











 THE CHRISTIAN WORKER
THE CHRISTIAN WORKER 1665678763032__30ro86
1665678763032__30ro86 Агрессия (4 класс)
Агрессия (4 класс) 1.1 + 1.2
1.1 + 1.2 История носового платка
История носового платка Поля листа
Поля листа Вкусное и красивое лакомство для неожиданных гостей
Вкусное и красивое лакомство для неожиданных гостей Добро пожаловать
Добро пожаловать Независимое распределение затрат в управленческом и регламентированном учете
Независимое распределение затрат в управленческом и регламентированном учете Абсолютные показатели оценки риска
Абсолютные показатели оценки риска Кипение
Кипение Страны Северной Европы
Страны Северной Европы Конструкция головы человека и её пропорции (6 класс)
Конструкция головы человека и её пропорции (6 класс) Энтеровирусная инфекция
Энтеровирусная инфекция Конвекция
Конвекция САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКИЕ ТРЕБОВАНИЯ К УСЛОВИЯМИ ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЯХ
САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКИЕ ТРЕБОВАНИЯ К УСЛОВИЯМИ ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЯХ Ассоциация «МЫ»
Ассоциация «МЫ»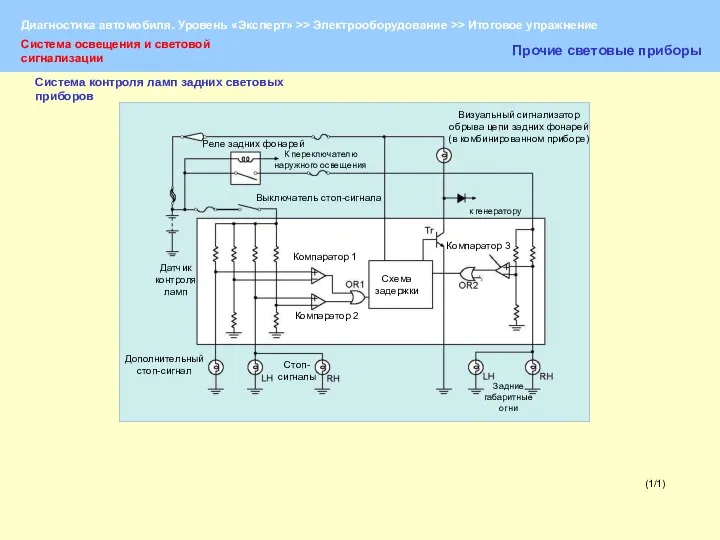 Диагностика автомобиля. Диагностирование осветительных приборов
Диагностика автомобиля. Диагностирование осветительных приборов Денис Васильевич Давыдов
Денис Васильевич Давыдов Рекомендую как пособие по медицинской генетике
Рекомендую как пособие по медицинской генетике Любимый семейный завтрак семьи Пьянковых
Любимый семейный завтрак семьи Пьянковых Доброта
Доброта О РЕЗУЛЬТАТАХ ЕГЭ в г. Сочи в 2011 ГОДУ
О РЕЗУЛЬТАТАХ ЕГЭ в г. Сочи в 2011 ГОДУ Психологические закономерности формирования личности в тренировочном процессе.
Психологические закономерности формирования личности в тренировочном процессе. Базовый межшкольный методический центр 26311
Базовый межшкольный методический центр 26311 Сложение и вычитание двузначных чисел 2 класс
Сложение и вычитание двузначных чисел 2 класс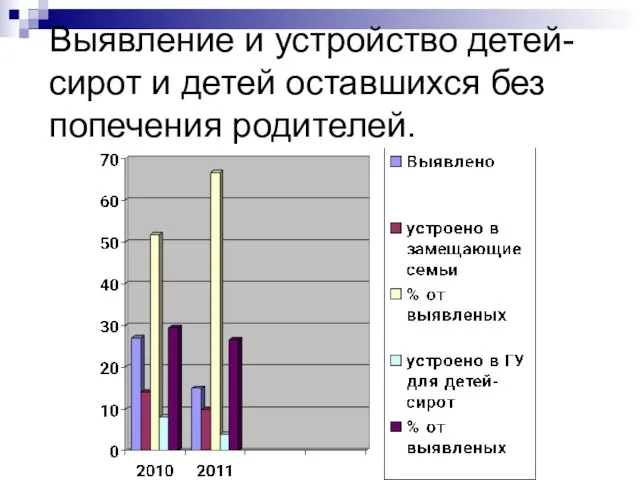 Выявление и устройство детей-сирот и детей оставшихся без попечения родителей.
Выявление и устройство детей-сирот и детей оставшихся без попечения родителей. Создание единого китайского государства
Создание единого китайского государства