Содержание
- 2. Цели и задачи. Определение диофантова уравнения Биография Диофанта Диофантовые уравнения первой степени Диофантовые уравнения высших степеней
- 3. Цели урока: Образовательные: 1.Познакомить учащихся с уравнениями, которые решаются в целых числах. 2.Организовать самостоятельный поиск решений
- 4. Задача. У мальчика было 50 р., на которые он хотел купить почтовые марки. В киоске имелись
- 5. Решение. Пусть марок по 4 р. х штук, по 3 р. – у штук. Всего имеется
- 6. Первым начал рассматривать такие уравнения Диофант (II – III вв. до нашей эры). Он рассматривал уравнения,
- 7. Диофант пытался ответить на следующий вопрос: «Дано уравнение с целыми коэффициентами. Имеет ли оно целые решения?»
- 8. Биографических данных о древнегреческом ученом-математике Диофанте из Александрии практически не сохранилось. До наших времен дошла лишь
- 9. Рассмотрим линейное диофантово уравнение 2х + 3у = 1. Найдите целые решения. Одно из решений –
- 10. При с = 0 уравнение (1) имеет вид ах + bу = 0 и называется однородным
- 11. В общем виде решением уравнения ах + bу = 0 является пара (-b n, an) Общим
- 12. Работа в группах. 1 группа. Предложите как можно подобрать частное решение уравнения 31х + 11 у
- 13. = 5·(31 – 11 · 2) – 4 · 11= 5 · 31+ 11· (- 14).
- 14. Группа 2. 6х + 9у = 2 (6х + 9у) ⫶ 3; 2 не делится на
- 15. Группа 4. 2х + 3у = 7 Частное решение х = 2; у = 1 Решение
- 16. Другой способ решения. 2х + 3у = 7 х = 3 – у + ; =
- 17. Диофантовы уравнения высших степеней. 1. Метод разложения на множители Задача 1. Доказать: что уравнение (x -
- 18. Задача 2. Решите уравнение в целых числах : 3ху + 2х + 3у = 0 Решение:
- 19. Проект учащихся «Метод бесконечного спуска»
- 20. 2. Метод «бесконечного спуска» Предположим, что уравнение имеет решение, строим бесконечный процесс, в то время как
- 21. Историческая справка. Метод бесконечного спуска изобрели, по-видимому, древнегреческие математики. Метод бесконечного спуска был существенно развит Пьером
- 22. Несмотря на отсутствие многих важных деталей в беглых заметках Ферма, в них отчетливо просматривался один из
- 23. Задача. Решите уравнение в целых числах: Решение. 1 4 - 2 - 8z13 = 0 2х3
- 24. Значит числа х1, у1 и z1 – тоже делятся на 2. Сколько бы раз мы не
- 25. Задание для самостоятельной работы. Доказать, что уравнение x 3 + 2y 3 + 4z 3 -
- 26. Другие методы решения диофантовых уравнений Задача: Доказать, что уравнение x 3 + y 3 + z
- 27. Домашнее задание. № 1 Решите в целых числах уравнение: а)8х + 14у = 32; б)6х –
- 28. За что ты можешь себя ПОХВАЛИТЬ? Что тебе УДАЛОСЬ на уроке? Над чем еще нужно ПОРАБОТАТЬ?
- 29. Удачи! Урок окончен!
- 31. Скачать презентацию




























 Студентське самоврядування як невід’ємна складова демократизації школи
Студентське самоврядування як невід’ємна складова демократизації школи Цвет - основа языка живописи
Цвет - основа языка живописи О Х Р А Н А Т Р У Д АТ Е М А:АТТЕСТАЦИЯ РАБОЧИХ МЕСТ ПО УСЛОВИЯМ ТРУДА.
О Х Р А Н А Т Р У Д АТ Е М А:АТТЕСТАЦИЯ РАБОЧИХ МЕСТ ПО УСЛОВИЯМ ТРУДА. Звуки [х], [х’], [ц]. Буквы Хх, Цц. Наблюдение особенностей правописания це,цы,ци
Звуки [х], [х’], [ц]. Буквы Хх, Цц. Наблюдение особенностей правописания це,цы,ци Особенности современного школьного образования в связи с введением ФГОС
Особенности современного школьного образования в связи с введением ФГОС Человек нравственно выше власти царя
Человек нравственно выше власти царя Структура курса
Структура курса Как животные готовятся к зиме
Как животные готовятся к зиме Человек и природа 13
Человек и природа 13 ОСВОЕНИЕ МИРОВОГО ОКЕАНА
ОСВОЕНИЕ МИРОВОГО ОКЕАНА Библиотечные интернет-сервисы: обслуживание без стен и границ
Библиотечные интернет-сервисы: обслуживание без стен и границ Balles de 0 à 10
Balles de 0 à 10 Репрезентативная система и темперамент человекаПрактико-ориентированное занятие для педагогов Детской школы искусств
Репрезентативная система и темперамент человекаПрактико-ориентированное занятие для педагогов Детской школы искусств Банки и банковские услуги
Банки и банковские услуги Правописание суффиксов прилагательных
Правописание суффиксов прилагательных Растения Подмосковья
Растения Подмосковья Конкурс «Системы качества подготовки выпускников образовательных учреждений профессионального образования »2000-2008 гг.www.usr.misis.ru
Конкурс «Системы качества подготовки выпускников образовательных учреждений профессионального образования »2000-2008 гг.www.usr.misis.ru Защита объектов ТХНГ от коррозии. Анализ графитопластовых заземлителей
Защита объектов ТХНГ от коррозии. Анализ графитопластовых заземлителей Подарки ВИП
Подарки ВИП Город-сказка
Город-сказка Ценные бумаги
Ценные бумаги Презентация на тему Основы предпринимательской деятельности
Презентация на тему Основы предпринимательской деятельности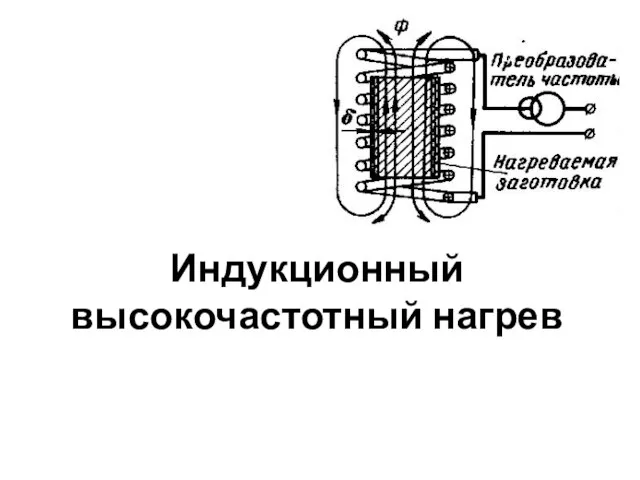 Индукционные печи
Индукционные печи О Канаде
О Канаде Презентация на тему Международные отношения в период между мировыми войнами
Презентация на тему Международные отношения в период между мировыми войнами Задачи на 2014-2015 учебный год (4 класс) ФГОС
Задачи на 2014-2015 учебный год (4 класс) ФГОС Рекомендации РНМОТ и ОССН по диагностике и лечению миокардитов
Рекомендации РНМОТ и ОССН по диагностике и лечению миокардитов «Необходимо подготовить ребят к профессиональной деятельности – с учетом задач модернизации и инновационного развития страны.
«Необходимо подготовить ребят к профессиональной деятельности – с учетом задач модернизации и инновационного развития страны.