Содержание
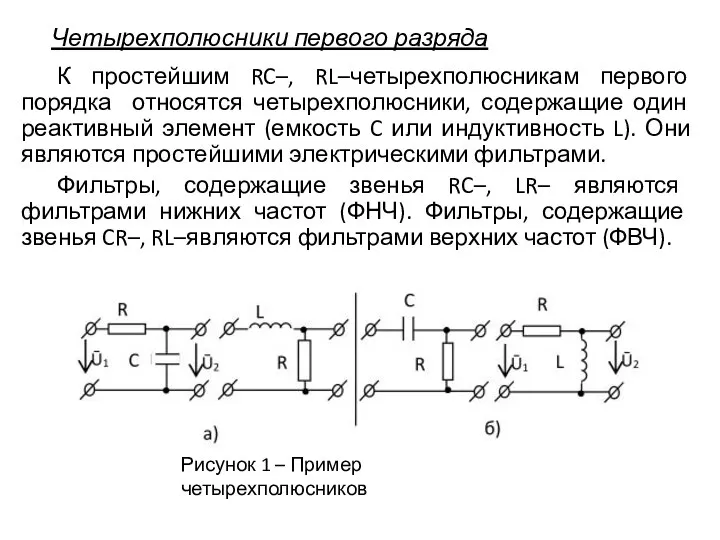
- 2. Четырехполюсники первого разряда К простейшим RC–, RL–четырехполюсникам первого порядка относятся четырехполюсники, содержащие один реактивный элемент (емкость
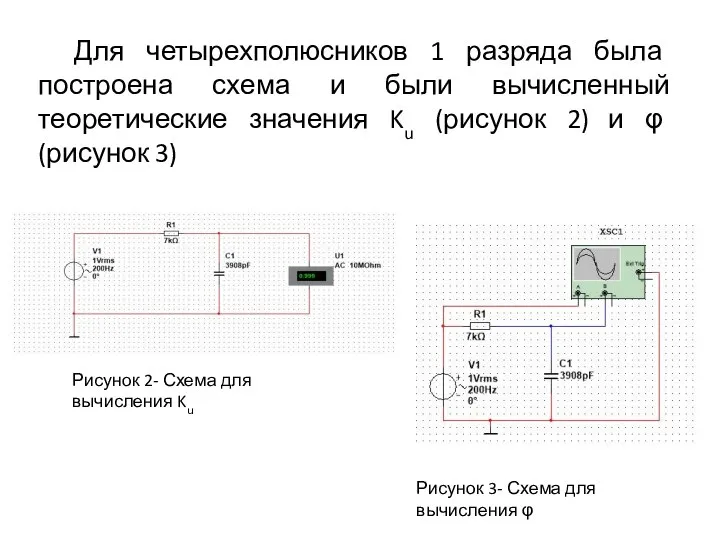
- 3. Для четырехполюсников 1 разряда была построена схема и были вычисленный теоретические значения Ku (рисунок 2) и
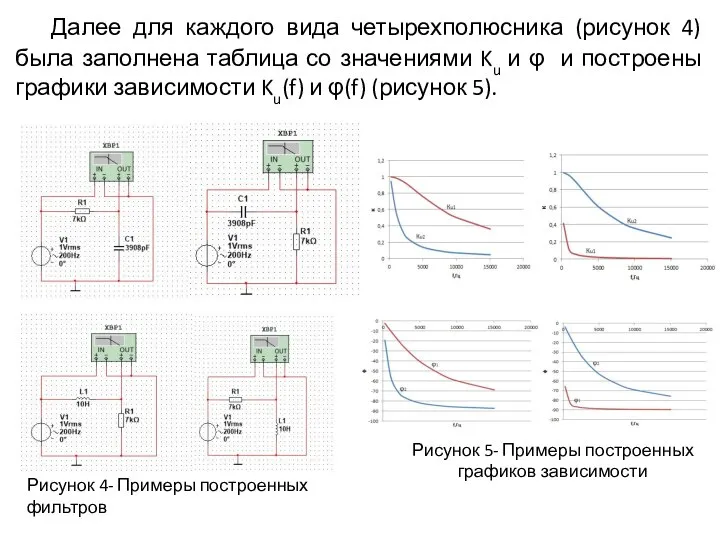
- 4. Далее для каждого вида четырехполюсника (рисунок 4) была заполнена таблица со значениями Ku и φ и
- 5. Многозвенные RC и LC-фильтры Элементы, входящие в состав фильтров, имеют одинаковые параметры. Но в некоторых случаях
- 6. Были смоделированы однозвенные (рисунок 7) и двухзвенные (рисунок 8) фильтры нижних частот и зафиксированы АЧХ при
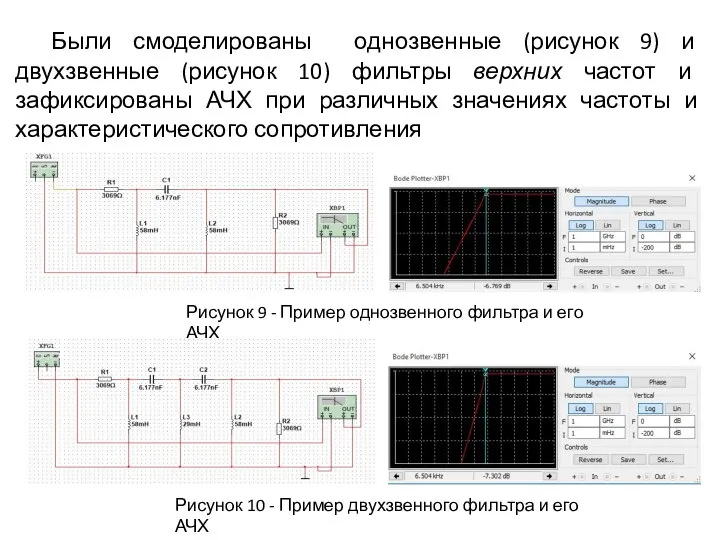
- 7. Были смоделированы однозвенные (рисунок 9) и двухзвенные (рисунок 10) фильтры верхних частот и зафиксированы АЧХ при
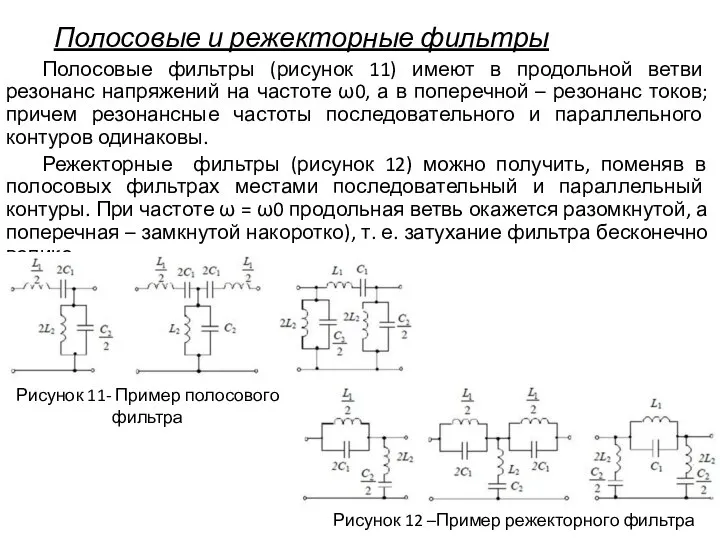
- 8. Полосовые и режекторные фильтры Полосовые фильтры (рисунок 11) имеют в продольной ветви резонанс напряжений на частоте
- 9. По заданным данным была вычислена центральная частота, далее построен двухконтурный полосовой фильтр (рисунок 13) и зафиксировано
- 10. По заданным данным была вычислена центральная частота, далее построен трехконтурный режекторный фильтр (рисунок 14) и зафиксировано
- 11. Синтезирование фильтров низких и высоких частот методами Баттерворта и Чебышева Процедура синтеза электронного фильтра включает в
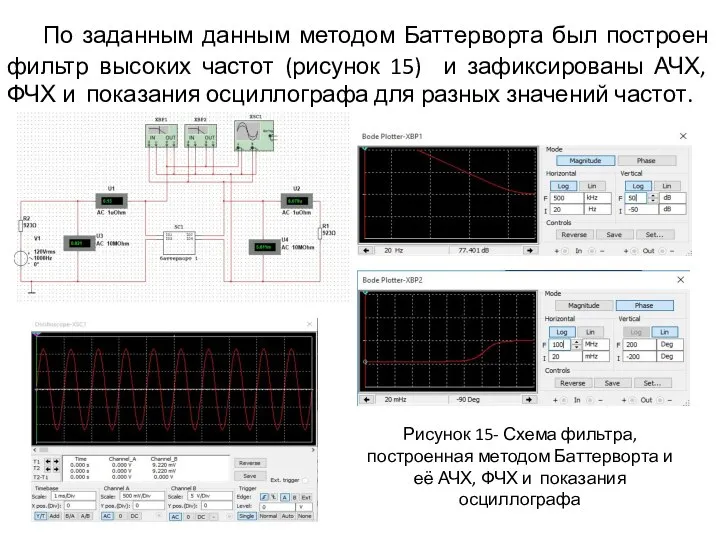
- 12. По заданным данным методом Баттерворта был построен фильтр высоких частот (рисунок 15) и зафиксированы АЧХ, ФЧХ
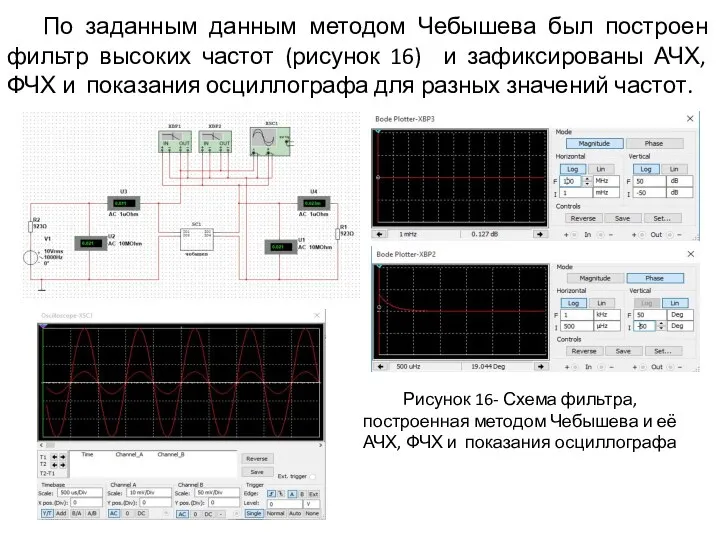
- 13. По заданным данным методом Чебышева был построен фильтр высоких частот (рисунок 16) и зафиксированы АЧХ, ФЧХ
- 15. Скачать презентацию





 Номенклатура алканов разветвлённого строения
Номенклатура алканов разветвлённого строения Симметрия и движение (9 класс)
Симметрия и движение (9 класс) Творческий проект
Творческий проект Составное глагольное сказуемое
Составное глагольное сказуемое Бартоломео Франческо Растрелли
Бартоломео Франческо Растрелли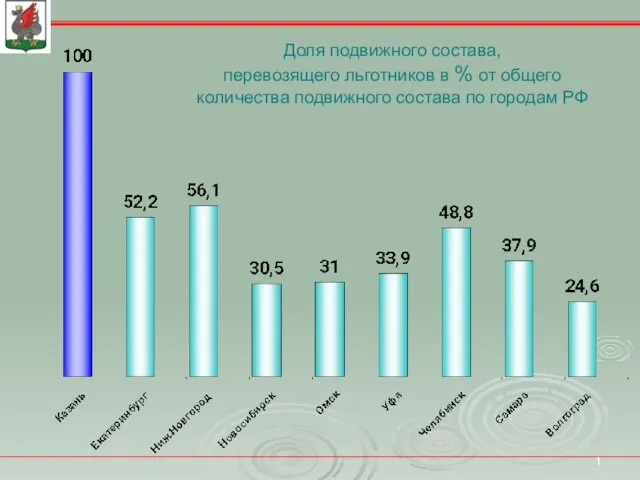 Доля подвижного состава, перевозящего льготников в % от общего количества подвижного состава по городам РФ
Доля подвижного состава, перевозящего льготников в % от общего количества подвижного состава по городам РФ О компании
О компании Конституция - основной закон государства
Конституция - основной закон государства Интересное проектирование – делимся опытом! Траверса для контейнера САО тип I и тип II
Интересное проектирование – делимся опытом! Траверса для контейнера САО тип I и тип II Диаграмма Ишикава. Алгоритм формирования диаграммы
Диаграмма Ишикава. Алгоритм формирования диаграммы Оплата труда гражданских служащих: новые подходы
Оплата труда гражданских служащих: новые подходы Добро пожаловать!!
Добро пожаловать!! Опыт работы администрации городского округа «Город «Хабаровск» в сфере профилактики социального сиротства, безнадзорности нес
Опыт работы администрации городского округа «Город «Хабаровск» в сфере профилактики социального сиротства, безнадзорности нес Скажи мне, как тебя зовут...
Скажи мне, как тебя зовут... Тема проекта:“Диета: за и против.”
Тема проекта:“Диета: за и против.” Культурное растение: «Чай»
Культурное растение: «Чай» СОХРАНИМ ОСТРОВА ДИКОЙ ПРИРОДЫ В ОКЕАНЕ ЦИВИЛИЗАЦИИ
СОХРАНИМ ОСТРОВА ДИКОЙ ПРИРОДЫ В ОКЕАНЕ ЦИВИЛИЗАЦИИ Ребята, давайте жить дружно!
Ребята, давайте жить дружно! Учет движения товаров. Приходные и расходные товарные операции
Учет движения товаров. Приходные и расходные товарные операции Лабораторный практикум Excel
Лабораторный практикум Excel Школьный этикет
Школьный этикет Алфавит в стихах
Алфавит в стихах Современное выставочное пространство Санкт-Петербурга
Современное выставочное пространство Санкт-Петербурга Драгоценные и поделочные камни - соединения кремния
Драгоценные и поделочные камни - соединения кремния Формула сайта:Успешный интернет-магазин от А до Я
Формула сайта:Успешный интернет-магазин от А до Я Factors Driving Industry Change
Factors Driving Industry Change  «Создание ароматических композиций из эфирных масел в условиях малой химической лаборатории»
«Создание ароматических композиций из эфирных масел в условиях малой химической лаборатории» Презентация на тему Как вести себя в конфликтной ситуации
Презентация на тему Как вести себя в конфликтной ситуации