Слайд 2Таким образом, и до, и после взаимодействия нейтрона с ядром имеются свободный

нейтрон и одно и то же ядро, и единственным результатом такого взаимодействия является лишь то, что кинетические энергии исходного и испущенного нейтронов неодинаковы: энергия испускаемого нейтрона в подавляющем большинстве случаев оказывается ниже энергии исходного нейтрона. Кроме того, направления движения исходного и испускаемого нейтронов также неодинаковы.
Слайд 3Внешне такое взаимодействие выглядит не как ядерное, а скорее как обычное механическое

соударение нейтрона с ядром, в результате которого нейтрон передает ядру часть своей кинетической энергии, меняя при этом свою скорость и направление движения.
Многократно повторяемые акты таких соударений в классической механике, как известно, называют рассеяниями. По аналогии с механическими рассеяниями нейтронные реакции подобного типа называют реакциями рассеяния.
Слайд 4Склонностью к реакции рассеяния, как и склонностью к радиационному захвату, обладают все

(без исключения) известные нуклиды, хотя и в различной степени.
Для реакторщика важно знать, ядра каких элементов наделены Природой этой склонностью к рассеянию, поскольку в тепловом реакторе за счёт реакций рассеяния идёт процесс уменьшения кинетической энергии нейтронов при их перемещении в среде активной зоны. Этот процесс коротко именуется замедлением нейтронов. Поэтому ядра - хорошие рассеиватели нейтронов, - обладающие пониженной склонностью к радиационному захвату, как правило, оказываются хорошими замедлителями нейтронов.
Слайд 5Например, ядра атомов водорода (1Н), дейтерия (2D), бериллия (9Be), углерода (12С), кислорода

(16О), циркония (91Zr) и ряд других ядер со слабыми захватными свойствами и сильно выраженной склонностью к рассеянию являются хорошими замедлителями рождаемых в реакторе быстрых нейтронов.
Слайд 6И ещё одна аналогия ядерного рассеяния с механическим: рассеяние может быть упругим

и неупругим, причём, критерии оценки упругости рассеяния в обоих случаях одинаковы:
- если суммы кинетических энергий ядра и нейтрона до и после рассеяния равны между собой
(Ея + Ен)до = (Ея + Ен)после ,
рассеяние называют упругим.
Слайд 7
Иначе говоря, энергетическое состояние и структура ядра до и после рассеяния остаются

неизменными;
Слайд 8- если же сумма кинетических энергий ядра и нейтрона после рассеяния оказывается

ниже, чем их сумма до рассеяния,
(Ея + Ен)до > (Ея + Ен)после ,
рассеяние называют неупругим.
Слайд 9Из этого не следует, что при неупругом рассеянии нарушается закон сохранения энергии:

просто разница сумм кинетических энергий до и после рассеяния затрачивается на изменение внутренней структуры ядра подобно тому, как при неупругом механическом соударении тел (например, свинцовых шариков) суммарное изменение их кинетической энергии расходуется на их деформацию.
Слайд 10Отметим одну важную закономерность ядерного рассеяния:
- упругое рассеяние в большей степени

свойственно лёгким ядрам (с атомной массой А < 20) при взаимодействии их с нейтронами сравнительно небольших кинетических энергий (Е < 0.1 МэВ), в то время как к реакциям неупругого рассеяния более склонны тяжёлые ядра при взаимодействии с нейтронами больших (Е > 1 МэВ) энергий.
Слайд 11Реакция деления.
Третий способ выхода возбуждённого составного ядра в более устойчивые образования

- деление его на две, три или даже более протонно-нейтронных комбинации, называемые осколками деления.
Слайд 12Обозначение: (n, f)
Обозначение сечения: σf, ∑f
Уравнение реакции:

Слайд 13Примечание:
Основная реакция в результате которой освобождается ядерная энергия, получаемая в ядерных реакторах

Слайд 14В отличие от реакций радиационного захвата и рассеяния, к делению склонны далеко

не все известные ядра, а лишь некоторые (главным образом, чётно-нечётные) ядра тяжёлых элементов. Вот некоторые из них:
233U, 235U, 239Pu, 241Pu, 251Cf, ...
Слайд 15Наиболее важным из перечисленных нуклидов является 235U - основное топливо большинства существующих

ядерных реакторов. 235U делится нейтронами любых кинетических энергий, но лучше всего – нейтронами с малыми энергиями.
Слайд 16Вторым по значимости делящимся нуклидом является 239Pu - вторичное топливо в урановых

реакторах, воспроизводящееся в процессе их работы. Как и 235U, 239Pu делится нейтронами любых кинетических энергий, но наиболее эффективно – тепловыми нейтронами.
Слайд 17Третьим по значению делящимся нуклидом является чётно-чётный изотоп урана - (238U). Чётное

число нейтронов в его ядре даёт более устойчивую комбинацию, чем нечётное их число, благодаря чему деление 238U имеет пороговый характер: для инициации деления ядер 238U годны не любые нейтроны, а лишь нейтроны с энергиями выше Еп = 1.1 МэВ. (Говорят: Eп = 1.1 МэВ - энергетический порог деления ядер урана-238).
Слайд 18Три нейтронные реакции
Во-первых, это реакция типа (n,p) - то есть нейтронная реакция,

завершающаяся испусканием протона.
В результате этой реакции образуется изобара исходного ядра, поскольку протон уносит один элементарный заряд, а масса ядра практически не меняется (нейтрон привнесён, а равный ему по массе протон - унесён).
Слайд 19Обозначение: (n, p)
Обозначение сечения: σp, ∑p
Уравнение реакции:
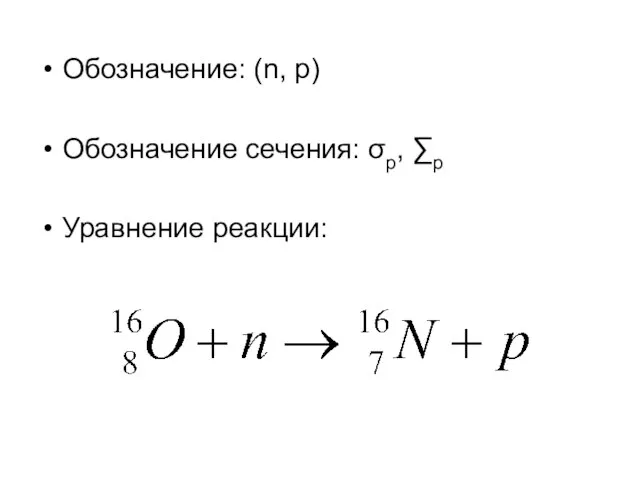
Слайд 20Примечание:
Реакция приводящая к активации воды первого контура.

Слайд 21Во-вторых, это реакция типа (n,α) - то есть реакция, завершающаяся испусканием возбужденным

составным ядром α-частицы (лишённого электронной оболочки ядра атома гелия 4He), в результате которой массовое число результирующего ядра снижается на 3 а.е.м. сравнительно с массой исходного ядра, а протонный заряд уменьшается на 2 единицы.
Слайд 22Обозначение: (n, α)
Обозначение сечения: σα, ∑α
Уравнение реакции:
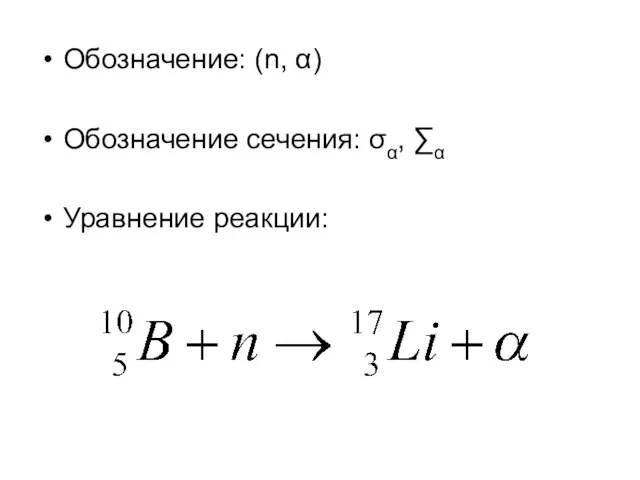
Слайд 23Примечание:
Поглощение нейтронов в регулирующих стержнях, выполненных из бора.
Регистрация замедленных нейтронов.

Слайд 24И, наконец, это реакция типа (n,2n) - то есть реакция с испусканием

возбуждённым составным ядром двух нейтронов, в результате которой образуется изотоп исходного элемента, на единицу меньшей массы сравнительно с массой исходного ядра.
Слайд 25Обозначение: (n, 2n)
Обозначение сечения: σ2n, ∑2n
Уравнение реакции:

Слайд 26Примечание:
Используется для регистрации плотности потока нейтронов с энергией выше пороговой.

Слайд 27Реакция с испусканием нейтронов под действием α-излучения
Обозначение: (α, n)
Обозначение сечения: σ(α,n), ∑(α,n)

Уравнение реакции:
Слайд 28Примечание
Используется для получения нейтронов, применяемых при физическом пуске реактора.

Слайд 29Фотонейтронные реакции
Обозначение: (γ, n)
Обозначение сечения: σ(γ,n), ∑(γ,n)
Уравнение реакции:

Слайд 30Примечание
Реакция фоторасщепления дейтерия, содержащегося в воде, используемой в качестве теплоносителя.
Имеет определенное значение

для увеличения числа нейтронов перед физическим пуском реактора.
Слайд 31Сечения поглощения
Обозначим полное эффективное сечение взаимодействия нейтрона с ядром σt.
После взаимодействия нейтрон

может лидо рассеется, либо поглотится.
Вероятность прохождение той или иной реакции характеризуется своими сечениями.
Слайд 32Обозначим:
σs – микроскопическое сечение упругого рассеяния
σis – микроскопическое сечение не упругого рассеяния
σa

– микроскопическое сечение поглощение нейтрона ядром
Слайд 33Тогда
σt = σs + σin + σa = σis + σa ,

где
σis = σs + σin – суммарное сечение упругого и не упругого рассеяния
Слайд 34Вспомним σ Nv = ∑, тогда
∑t = ∑is + ∑a, где
∑t =

σt Nv - полное макроскопическое эффективное сечение взаимодействия нейтрона с ядром данного нуклида;
∑is = σis Nv - полное макроскопическое эффективное сечение реакции рассеяния нейтрона ядрами данного нуклида
∑a = σa Nv - полное макроскопическое эффективное сечение реакции поглощения нейтрона ядрами данного нуклида
Слайд 35Поглощение нейтронов происходит в реакциях (n, γ); (n, α); деление ядра и

д.р.
С учетом возможностей
σa = σγ + σf + σα
σγ – микроскопическое сечение реакции радиационного захвата (n, γ);
σf – микроскопическое сечение реакции деления (n, f);
σα - микроскопическое сечение реакции с испусканием α частицы (n, γ);
Слайд 36Для энергии нейтронов < 5 МэВ у большинства ядер различных нуклидов реакцией

поглощения является радиационный захват нейтронов
(σa = σγ)
Для ядер нуклидов (232U, 238U, 239Pu и т.д.) наряду с радиационным захватом идет реакция деления
σa = σγ + σf
Слайд 37Вспомним ∑ = σ Nv, тогда
∑а = ∑γ + ∑f + ∑α,

где
∑i = σi Nv (при i= γ, f, α) – макроскопические сечения i-ой ядерной реакции.
Слайд 38Отметим, что Cv=∑φ и из определения ∑а , ∑γ , ∑is следует,

что за 1 секунду в 1 м3 вещества при плотности нейтронов φ происходит ∑а φ – поглощений нейтронов, ∑is φ – актов рассеяния нейтронов, ∑γ φ – делений ядер.
Слайд 39
Средний свободный пробег нейтронов λi – среднее расстояние, проходимое нейтроном между двумя

актами выхода i-ой реакции с ядрами вещества.
Слайд 40За 1 секунду в 1 м3 вещества совершается Сvi актов взаимодействия с

выходом i-ой реакции, при этом длина пути, пройденного нейтроном, равна плотности потока нейтронов φ, тогда среднее расстояние между двумя актами взаимодействий с учетом
Сv = σ Nv n V= σ Nv φ = ∑ φ
λi = φ / Cvi = 1/ ∑i
Слайд 41Если взаимодействие нейтрона с ядром является реакция рассеяния, то λi = λis,

где λis = 1/ ∑is и равняется среднему расстоянию, проходимому нейтроном между двумя последовательными рассеивающими столкновениями.
Величину λis называют средним свободным пробегом рассеяния (длиной рассеяния)
Слайд 42Аналогично для реакций поглощения нейтрона ядром λi = λа, где λа =

1/ ∑а ,
Равняется среднему полному пути, проходимому нейтроном в среде от рождения до его поглощения и называется средним свободным пробегом до поглощения (длиной поглощения)
Слайд 43Полная средняя длина свободного пробега равна
λt = 1/ ∑t
1/λt = 1/λа +

1/λis
∑t = ∑a + ∑is
Слайд 44Микроскопическое сечение различных реакций существенно зависит от энергии нейтрона.
С уменьшением энергии нейтронов

сечения увеличиваются. Это связано с волновыми свойствами нейтрона.
В ядерных реакторах энергия нейтронов изменяется в весьма широком диапазоне от 107 до 10-3 МэВ.
Слайд 45Коэффициент размножения и нейтронный цикл в реакторе на тепловых нейтронах
Активная зона реактора

на тепловых нейтронах состоит из слабообогащенного ядерного топлива, замедлителя, теплоносителя, конструкционных материалов, регулирующих стержней.
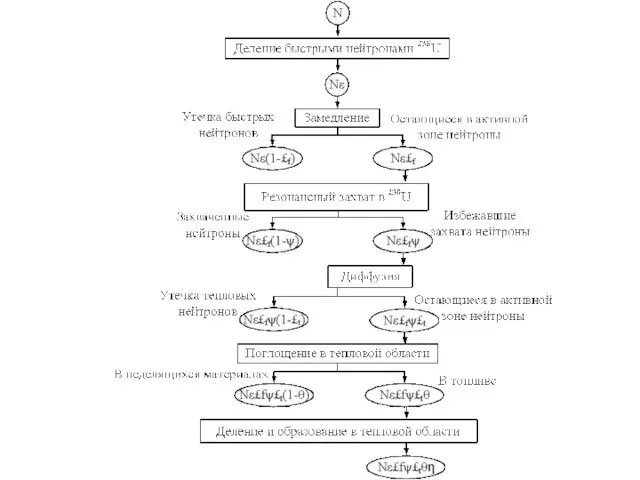
Слайд 46Рассмотрим нейтронный цикл в реакторе, где топливо содержит уран. Допустим, что в

некоторый момент времени в активной зоне в результате деления 235U образовалось N быстрых нейтронов.
Слайд 47Образовавшиеся в результате делений ядер 235U нейтроны в среднем имеют энергию выше

порога деления ядер 238U, поэтому в процессе поглощения ядрами 238U эти нейтроны могут вызвать их деление. Кроме того, некоторое число быстрых нейтронов может вызвать деление ядер 235U. В этой области энергий сечения деления 235U и 238U примерно равны, но ввиду малого содержания в активной зоне 235U
Слайд 48В этой области энергий сечения деления 235U и 238U примерно равны, но

ввиду малого содержания в активной зоне 235U по сравнению с содержанием 238U этот эффект мал. При делении 238U на один поглощенный быстрый нейтрон выделяется в среднем 2,4 новых быстрых нейтрона, поэтому в результате этого процесса число нейтронов несколько возрастает.
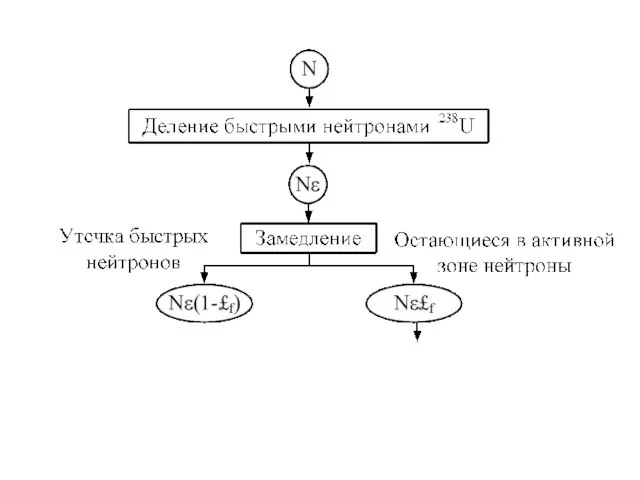
Слайд 49Это увеличение учитывается коэффициентом размножения на быстрых нейтронах в, который показывает, во

сколько раз увеличивается число нейтронов деления 235U из-за дополнительного деления ядер 238U быстрыми нейтронами.
Слайд 50Значение ε зависит, от состава и геометрии активной зоны. Обычно ε≈1,02…1,03. В

результате этого процесса общее число нейтронов в активной зоне будет равно Nε. Однако часть быстрых нейтронов может вылететь из активной зоны.
Слайд 51Этот процесс учитывается параметром £f – вероятностью избежания утечки быстрых нейтронов, равной

доле быстрых нейтронов, избежавших утечки из активной зоны. Таким образом, из-за утечки быстрых нейтронов в активной зоне остается Nε£f нейтронов.
Слайд 53Быстрые нейтроны слабо поглощаются ядрами, претерпевая неупругое рассеяние на ядрах 238U и

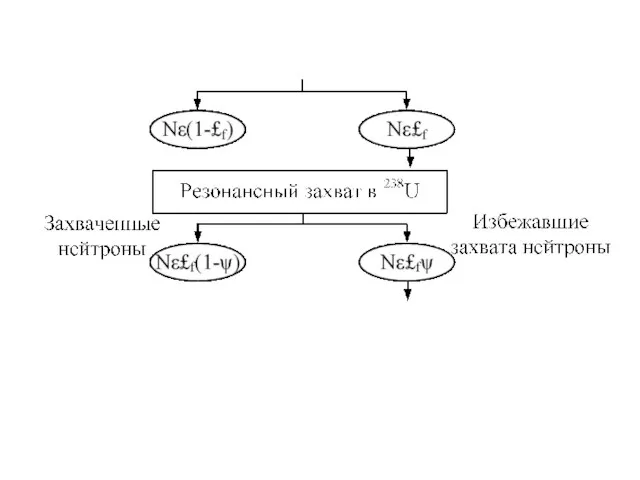
упругое рассеяние на ядрах замедлителя, и в результате замедляются. В процессе замедления имеется определенная вероятность поглощения нейтронов ядрами 238U без деления в резонансной области энергии.
Слайд 54Отметим, что по сравнению с резонансным поглощением поглощение нейтронов нерезонансных энергий незначительно.

Из-за резонансного поглощения число нейтронов, достигающих тепловой энергии, будет уменьшаться.
Слайд 55Этот эффект учитывается коэффициентом ψ – вероятностью избежать резонансного захвата, который равен

отношению числа быстрых нейтронов, избежавших захвата в резонансной области энергии и достигших тепловой энергии, к общему числу быстрых нейтронов.
Слайд 56Очевидно, что ψ<1. Значение ψ зависит от типа замедлителя, степени обогащения ядерного

топлива, относительных количеств топлива и замедлителя и их взаимного расположения. Таким образом, в результате всех описанных процессов из N первоначально быстрых нейтронов в активной зоне образуется Nε£f ψ тепловых нейтронов.
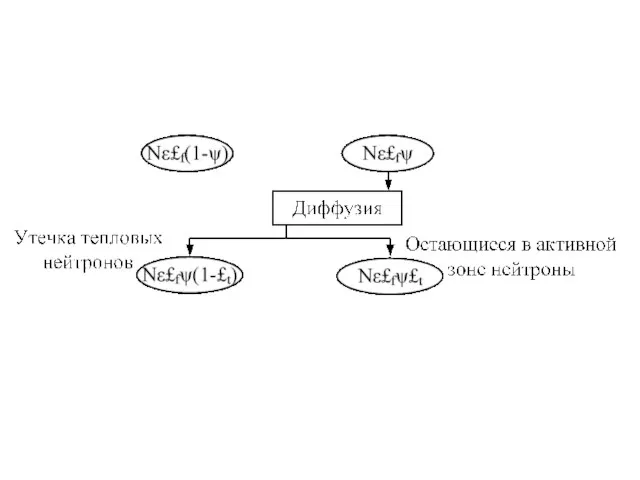
Слайд 58Тепловые нейтроны диффундируют в объеме активной зоны и могут вылететь за ее

пределы. Этот эффект учитывается вероятностью избежать утечки тепловых нейтронов £t , равной доле тепловых нейтронов, избежавших утечки из активной зоны. С учетом этого процесса в активной зоне остается Nε£f ψ £t тепловых нейтронов, которые диффундируют до тех пор, пока не поглотятся.
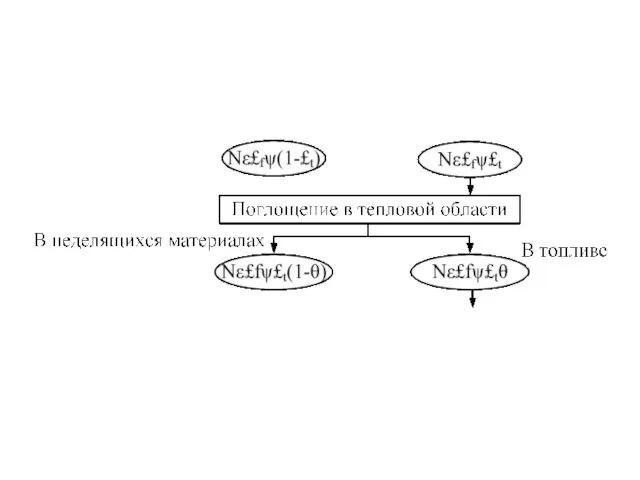
Слайд 60Вероятность того, что тепловой нейтрон поглотится в уране, а не в других

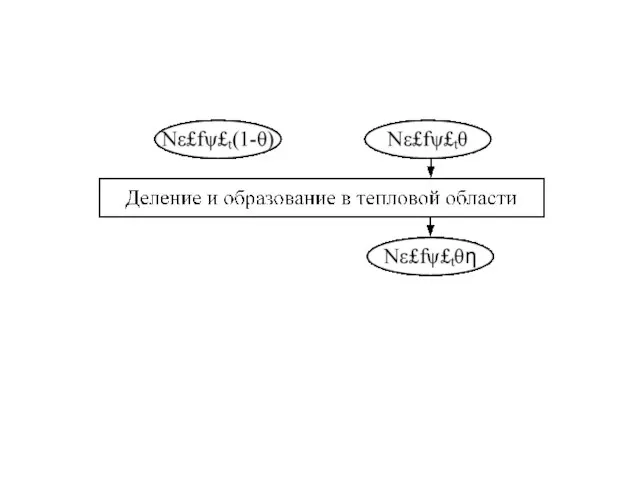
веществах, определяется коэффициентом использования тепловых нейтронов в, который равен отношению числа тепловых нейтронов, поглощенных в уране, к общему числу тепловых нейтронов, поглощенных материалами активной зоны. Общее число тепловых нейтронов, поглощенных в уране, равно Nε£f ψ £t θ.
Слайд 62На один захваченный ураном тепловой нейтрон в среднем в результате деления 235U

выделяется η быстрых нейтронов, тогда из N быстрых нейтронов, имевшихся в начале цикла, получается Nε£f ψ £t θ η таких же быстрых нейтронов следующего поколения. Следовательно, из определения эффективного коэффициента размножения получим kэф = Nε£f ψ £t θ η / N = ε£f ψ £t θ η.
Слайд 65Систему бесконечных больших размеров нейтроны не могут покинуть, и вероятность избежать утечки

равна единице, т. е. £f = 1, £t = 1, тогда коэффициент размножения для системы бесконечного размера
k∞ = ηεψθ
Слайд 66k∞ = ηεψθ
Данную формулу часто называют формулой четырех сомножителей, она показывает зависимость

k∞ от различных факторов, определяющих развитие цепной реакции деления в размножающих системах, в которых ядерным топливом является уран.
Слайд 67Совмещаю формулу четырех сомножителей и kэф, получаем
kэф = k∞ £f £t
Активная

зона находится в критическом состоянии, если kэф = 1, тогда
k∞ £f £t = 1
В реальных активных зонах всегда существует утечка нейтронов, поэтому £f £t <1, отсюда kэф < k∞ .
Слайд 68Таким образом, для того чтобы в активной зоне имела место самоподдерживающаяся цепная

реакция деления, значение k∞ , должно быть несколько больше единицы. Значение k∞ зависит от состава и взаимного расположения материалов активной зоны и показывает возможность осуществления самоподдерживающейся цепной реакции деления в активной зоне при заданной утечке нейтронов.

















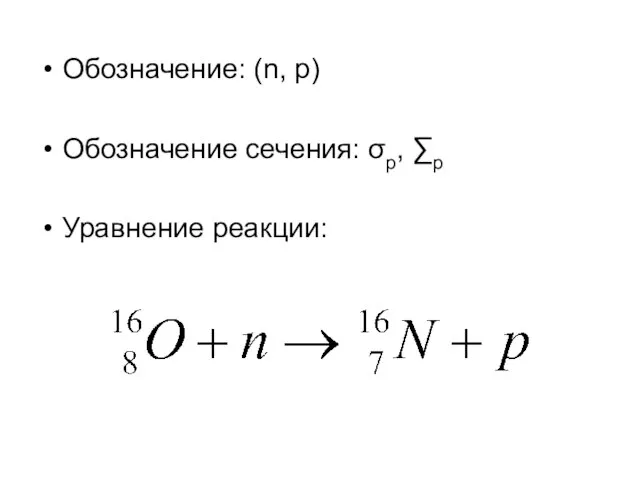


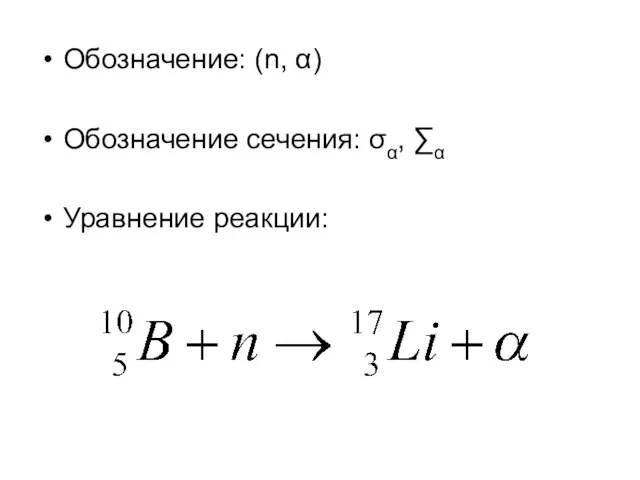








































 Системы лояльности: современные тенденции развития
Системы лояльности: современные тенденции развития Теорема Виета доказательство
Теорема Виета доказательство Словообразовательные гнёзда полисемантичных имён существительных в русском и белорусском языках
Словообразовательные гнёзда полисемантичных имён существительных в русском и белорусском языках СМАЗКИ КАНАТНЫЕ
СМАЗКИ КАНАТНЫЕ Приемы рисования геометрических фигур
Приемы рисования геометрических фигур Metal-Insulator-Semiconductor and Metal-Insulator-Metal Structures
Metal-Insulator-Semiconductor and Metal-Insulator-Metal Structures "Я ЛЮБЛЮ ТЕБЯ,РОССИЯ!" Игра "Звездный час" (для учащихся 3-4классов)
"Я ЛЮБЛЮ ТЕБЯ,РОССИЯ!" Игра "Звездный час" (для учащихся 3-4классов) Три кита в музыке
Три кита в музыке Сбор изображений для тренировки системы распознавания номеров машин
Сбор изображений для тренировки системы распознавания номеров машин Презентация на тему Состав ядра. Ядерные силы (11 класс)
Презентация на тему Состав ядра. Ядерные силы (11 класс) Понятие мотивации. Мотивация по Риссу. Нейрологические уровни Дилтса. Модель ценностей Грейвза
Понятие мотивации. Мотивация по Риссу. Нейрологические уровни Дилтса. Модель ценностей Грейвза Финансовая политика РФ
Финансовая политика РФ Дециметр
Дециметр Материки и океаны
Материки и океаны Конституционное право - ведущая отрасль в правовой системе Российской Федерации. Лекция 1
Конституционное право - ведущая отрасль в правовой системе Российской Федерации. Лекция 1 Александр Родченко
Александр Родченко Спектры.Спектральный анализОткрытый урок
Спектры.Спектральный анализОткрытый урок Лепка фигуры человека
Лепка фигуры человека ОПСиП_ Семенова ПО-3
ОПСиП_ Семенова ПО-3 Градусная сеть на глобусе и географической карте
Градусная сеть на глобусе и географической карте Международный Юридический институт приглашает всех желающих на День Открытых дверей!
Международный Юридический институт приглашает всех желающих на День Открытых дверей! Страхование непредвиденных расходов автовладельцев полис «РЕСОавто ПОМОЩЬ»
Страхование непредвиденных расходов автовладельцев полис «РЕСОавто ПОМОЩЬ» Бюджет доходов и расходов БДР/P&L
Бюджет доходов и расходов БДР/P&L Лексика
Лексика אילו המצאות חדשות הומצאו בישראל ובעולם ?במאה ה?21 -במה תרומתם לאנושות
אילו המצאות חדשות הומצאו בישראל ובעולם ?במאה ה?21 -במה תרומתם לאנושות Главные и второстепенные члены предложения
Главные и второстепенные члены предложения Основные причины ухудшения зрения школьника
Основные причины ухудшения зрения школьника Качество и качества Власти: восприятие населения
Качество и качества Власти: восприятие населения