Содержание
- 2. Определение: Два уравнения называются равносильными, если их множества решений равны
- 3. Теорема 1: Пусть уравнение f(x) = g(x)задано на множестве X и h(x) – выражение, определенное на
- 4. Доказательство: Обозначим через Т1 множество решений уравнения (1), а через Т2 множество решений уравнения (2). Тогда
- 5. Пусть число а – корень уравнения (1). Тогда а Є Т1 и при подстановке в уравнение
- 6. Итак, доказано, что каждый корень уравнения (1) является корнем уравнения (2), т.е. Т1СТ2. Пусть, теперь b
- 7. Итак, доказано, что каждый корень уравнения (2) является и корнем уравнения (1), т.е. Т2 С Т1.
- 8. Теорема 2: Пусть уравнение f(x) = g(x) на множестве X и h (x) – выражение, определенное
- 9. Доказательство этой теоремы аналогично доказательству теоремы 1. Из теоремы 2 вытекает следствие, которое часто воспользуется при
- 13. Возьмем теперь уравнение х(х - 1) = 2х, хЄR. Иногда учащиеся решают его так: делят обе
- 16. Таким образом, множество решений данного уравнения состоит из двух чисел 0 и 3, т.е. имеет вид
- 18. Скачать презентацию















 Весёлая математика
Весёлая математика Асэнсаванне еўрапейскай культуры Новага часу асветнікамі Беларусі
Асэнсаванне еўрапейскай культуры Новага часу асветнікамі Беларусі ВЕТРЫ ЗЕМЛИ
ВЕТРЫ ЗЕМЛИ С днём пионерии
С днём пионерии Концепция рекламно-художественного оформления города
Концепция рекламно-художественного оформления города Михаил Пришвин. Школьная Робинзонада
Михаил Пришвин. Школьная Робинзонада Копия презентации на www.demos.su/integrat/secur.htm
Копия презентации на www.demos.su/integrat/secur.htm Презентация на тему Слово и слог 1 класс
Презентация на тему Слово и слог 1 класс Нужно помогать людям!!!!!!!!!!!!
Нужно помогать людям!!!!!!!!!!!! Арта. Юбилей
Арта. Юбилей Учебный проект
Учебный проект Вопросы от ученого кота
Вопросы от ученого кота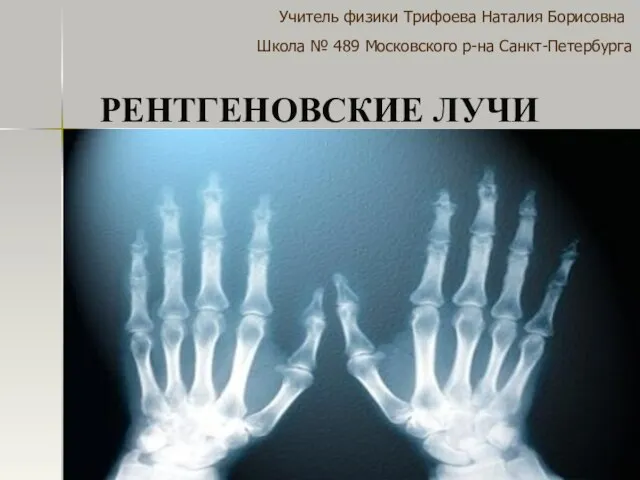 Презентация на тему РЕНТГЕНОВСКИЕ ЛУЧИ
Презентация на тему РЕНТГЕНОВСКИЕ ЛУЧИ  Всероссийский конкурс
Всероссийский конкурс Компетентностная задача №12. Поддержим отечественного производителя
Компетентностная задача №12. Поддержим отечественного производителя Степени сравнения наречий
Степени сравнения наречий 11
11 Контроль и регулирование
Контроль и регулирование  День России
День России Министерство экономического развития Российской Федерации Российская академия народного хозяйства и государственной службы пр
Министерство экономического развития Российской Федерации Российская академия народного хозяйства и государственной службы пр Презентация на тему Насекомые
Презентация на тему Насекомые  Развитие представлений личности по Рубинштейну С.Л
Развитие представлений личности по Рубинштейну С.Л Паустовский «Жильцы старого дома» 3 класс
Паустовский «Жильцы старого дома» 3 класс Карвинг
Карвинг Презентация
Презентация Презентация на тему Биосфера как единая экосистема Земли
Презентация на тему Биосфера как единая экосистема Земли Кафедра таможенного дела Магистерская диссертация Эффективность таможенно-тарифной политики в создании безбарьерной внешнетор
Кафедра таможенного дела Магистерская диссертация Эффективность таможенно-тарифной политики в создании безбарьерной внешнетор c_electron_config
c_electron_config