Различные виды уравнения прямой

Общее уравнение прямой
Уравнение Ax+By+C=0 (где A, B и C могут принимать любые значения, лишь бы коэффициенты A, B не были равны нулю оба сразу) представляет прямую линию.
Всякую прямую можно представить уравнением этого вида. Поэтому его называют общим уравнением прямой.

Ах+Ву+С=0
1) Если A=0, то уравнение представляет прямую, параллельную оси Ох (у= ).
Пример 1.
Графиком уравнения у=-10 является прямая, параллельная оси Ох и проходящая через точку (0;-10).

Ах+Ву+С=0
2) Если В=0, то уравнение представляет прямую, параллельную оси Оу (х= ).
Пример 2.
Графиком уравнения х=6 является прямая, параллельная оси Оу и проходящая через точку (6;0).

Ах+Ву+С=0
3) Когда В=0, то у=
Уравнение у=кх+m, где к= , а m= называется уравнением прямой с угловым коэффициентом к.
4) Если С=0, то есть уравнение Ах+Ву+С=0 не содержит свободного члена, то оно представляет прямую, проходящую через начало координат.

Ах+Ву+С=0
(у= , то есть у=кх – где к – угловой коэффициент прямой. Ясно, что к= , где Х0 и У0 координаты произвольной точки прямой, Х0=0).
х
у
у0
х0
1
0
1

Пример 3.
Составить уравнение прямой, изображенной на рисунке.
Решение.
Так как прямая проходит через начало координат, то она задается уравнением у=кх. Определим угловой коэффициент этой прямой. Возьмем к примеру точку А этой прямой, тогда к= , то есть к= . Значит, к=-2 и уравнение данной прямой имеет вид: у=-2х.
0
у
х
-1
1
1
-1
А
2

Пример 4.
Составить уравнение прямой, изображенной на рисунке.
Решение.
Данная прямая получена из прямой у=кх смещением последней на 3 ед. отрезка вверх вдоль оси Оу. Прямые у=кх и данная параллельны, следовательно, их угловые коэффициенты равны. Определив угловой коэффициент прямой у=кх (к= ), получим, что угловой коэффициент данной прямой равен -2. А так как данная прямая пересекает ось Оу в точке с ординатой 3, то в уравнении данной прямой (у=кх+m), к=-2, m=3. Искомое уравнение имеет вид у= =-2х+3.
у=кх
у
х
А

Теоремы
Уравнение изображенной прямой можно получить и иначе, если иметь ввиду следующие утверждения.
Теорема 1.
Если прямая отсекает на осях отрезки а и в (не равные нулю), то ее можно представить уравнением =1.

Теорема 2.
Уравнение =1 представляет прямую, отсекающую на осях (считая от начала координат) отрезки а и в.
Уравнение =1 называется уравнением прямой в отрезках (ясно, что а=0, в=0).

Вывод уравнения прямой в отрезках.
Уравнение прямой в отрезках легко получается либо из общего уравнения прямой, либо из уравнения прямой с угловым коэффициентом.
Пусть у=кх+m – уравнение прямой с угловым коэффициентом. Приведем его к виду =1.

у=кх+m
Для этого перенесем слагаемое кх в левую часть уравнения, изменив его знак на противоположный и разделим обе части полученного равенства на m. Получим следующее уравнение =1. Перепишем это уравнение в виде =1.
Учтем, что = . Следовательно, = . Обозначив буквой «а», а m – буквой «в» получим искомое уравнение прямой в отрезках =1.

Рассмотрим следующий пример
Пример 5.
Составить уравнение прямой, изображенной на рисунке.
Решение. Прямая отсекает отрезки -2 на оси Оу и 3 – на оси Ох. Поэтому ее уравнение можно записать так:1) =1 или =1. Из последнего уравнения можно получить уравнение прямой в общем виде и уравнение прямой с угловым коэффициентом.
у

Пример 5.
2) =1 6. 2х-3у=6. 2х-3у-6=0.
3) =1. = 1 2. у= -2.
В ответе можно записать любое из уравнений 1), 2) или 3).
Кроме того, уравнение прямой в отрезках удобно использовать для построения этой прямой на чертеже.

Уравнение прямой, проходящей через две точки.
Теперь, допустим, нужно записать уравнение прямой проходящей через две точки А (1;-2) и В (-1;4). Очевидно, что для решения этой задачи надо составить и решить систему уравнений
относительно к и m, где х1=1, у1=-2,
х2=-1, у2=4. И, найдя значения к и m, подставить их в уравнение у=кх+m. Всякий раз решать подобные задачи таким способом довольно-таки нерационально.
у2=кх2+m.
у1=кх1+m,

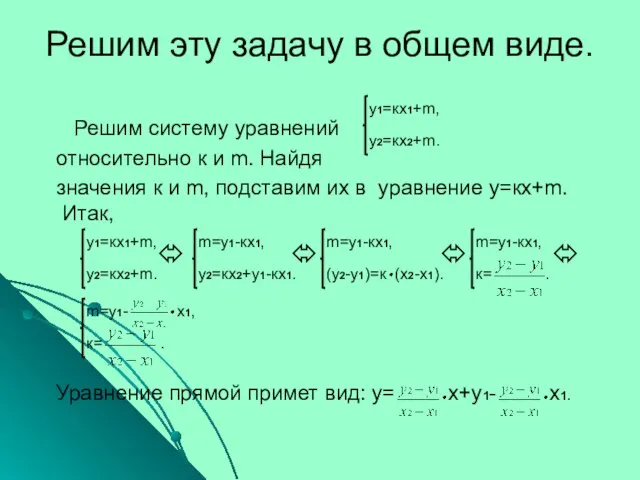
Решим эту задачу в общем виде.
Пусть требуется составить уравнение прямой, проходящей через две различные точки (х1;у1) и (х2;у2) такие, что х1=х2, у1=у2.
Так как прямая проходит через эти точки, то их координаты удовлетворяют уравнению прямой у=кх+m.

Решим эту задачу в общем виде.
Решим систему уравнений
относительно к и m. Найдя
значения к и m, подставим их в уравнение у=кх+m. Итак,
Уравнение прямой примет вид: у= х+у1- х1.
у2=кх2+m.
у1=кх1+m,
m=у1-кх1,
у2=кх2+у1-кх1.
m=у1-кх1,
у2=кх2+m.
у1=кх1+m,
к= .
(у2-у1)=к (х2-х1).
m=у1-кх1,
m=у1- х1,
к= .

Преобразуем его
у-у1= х- х1,
у-у1= (х-х1).
(у-у1) (х2-х1)=(у2-у1) (х-х1) (х2-х1) (у2-у1),
Мы получили уравнение прямой, проходящей через две различные точки (х1;у1) и (х2;у2), причем х1=х2, у1=у2.
,
,

(у-у1) (х2-х1)=(у2-у1) (х-х1)
А что если х2=х1 (при условии, что у2=у1) или у2=у1 (при условии, что х2=х1)?
В этом случае уравнение ( ) будет выглядеть так:
(у2-у1) (х-х1)=0 или (у-у1) (х2-х1)=0. Откуда получим уравнения: х=х1 или у=у1. То есть уравнения прямых, параллельных координатным осям.

В первом случае – уравнение прямой, параллельной оси Оу, а во втором случае – уравнение прямой, параллельной оси Ох.
у
х

Пример 6.
Записать уравнение прямой, проходящей через точки А (1;-2) и В (-1;4).
Решение.
Воспользуемся уравнением прямой, проходящей через две различные точки.
Перепишем его в виде
Теперь подставим в него координаты данных точек:
Итак, у=-3х+1 – уравнение прямой, проходящей через точки А(1;-2) и В (-1;4).
Ответ: у=-3х+1
(-6)
-3(х-1)=у+2.
у=-3х+1.

Рассмотрим задачу:
«Лежат ли точки А1 (-2;5), А2 (4;3), А3 (16;-1) на одной прямой?».
Решить ее можно так:
1) Составить уравнение прямой, проходящей, например, через точки А1 и А2.
2) Подставить координаты точки А3 в полученное уравнение, проверив тем самым, принадлежит ли точка А3 прямой, проходящей через точки А1 и А2.

Итак: «Лежат ли точки А1 (-2;5), А2 (4;3), А3 (16;-1) на одной прямой?»
Использование уравнения прямой, проходящей через две различные точки, значительно сокращает процесс поиска решения данной задачи. Положив в уравнении х=х3, у=у3 и, подставив координаты данных точек в равенство ,
получим: . Полученное равенство верное, следовательно, точки А1, А2 и А3 лежат на одной прямой .
Итак, использование различных видов уравнений прямой позволяет рационализировать поиск решения ряда задач.