Разные задачи повышенного уровня сложности на многогранники, цилиндры, косинус и шар

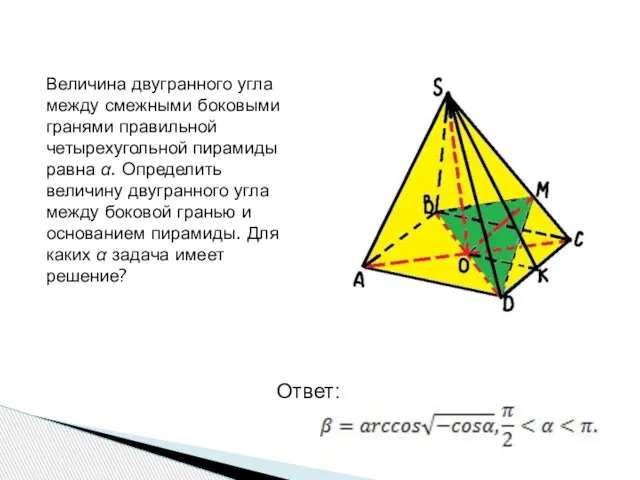
Величина двугранного угла между смежными боковыми гранями правильной четырехугольной пирамиды равна α. Определить величину двугранного угла между боковой гранью и основанием пирамиды. Для каких α задача имеет решение?
Ответ:

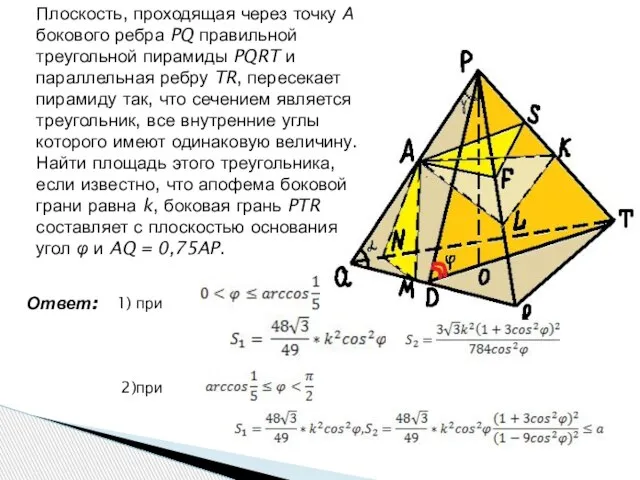
Плоскость, проходящая через точку А бокового ребра PQ правильной треугольной пирамиды PQRT и параллельная ребру TR, пересекает пирамиду так, что сечением является тре­угольник, все внутренние углы которого имеют одинаковую величину. Найти площадь этого треугольника, если известно, что апофе­ма боковой грани равна k, боковая грань PTR составляет с плоскостью основания угол φ и AQ = 0,75AP.
Ответ:
2)при
1) при

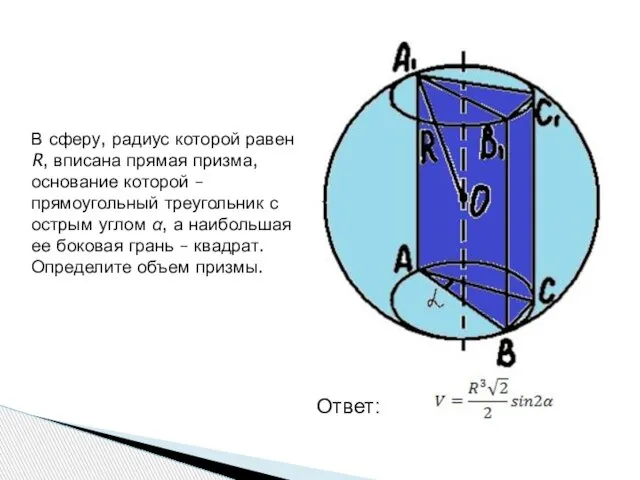
В сферу, радиус которой равен R, вписана прямая призма, основание которой – прямоугольный треугольник с острым углом α, а наибольшая ее боковая грань – квадрат. Определите объем призмы.
Ответ:

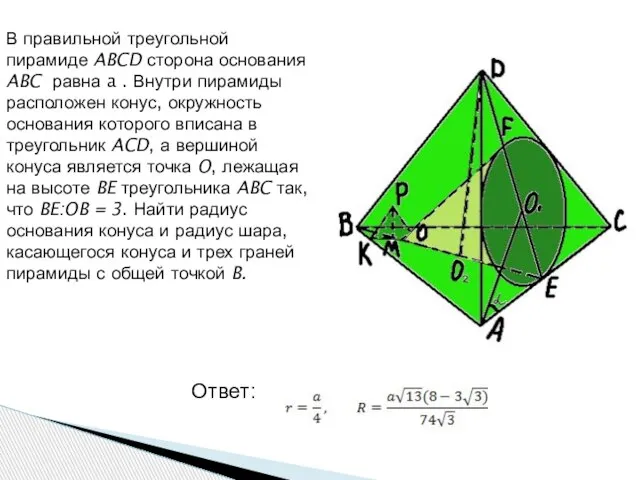
В правильной треугольной пирамиде ABCD сторона основания ABC равна a . Внутри пирамиды расположен конус, окружность основания которого вписана в треугольник ACD, а вершиной конуса является точка O, лежащая на высоте BE треугольника ABC так, что BE:OB = 3. Найти радиус основания конуса и радиус шара, касающегося конуса и трех граней пирамиды с общей точкой B.
Ответ:

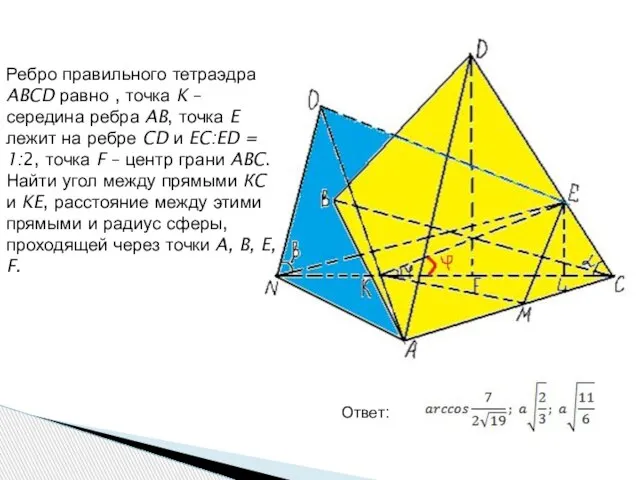
Ребро правильного тетраэдра ABCD равно , точка K – середина ребра AB, точка E лежит на ребре CD и EC:ED = 1:2, точка F – центр грани ABC. Найти угол между прямыми КC и KE, расстояние между этими прямыми и радиус сферы, проходящей через точки A, B, E, F.
Ответ:

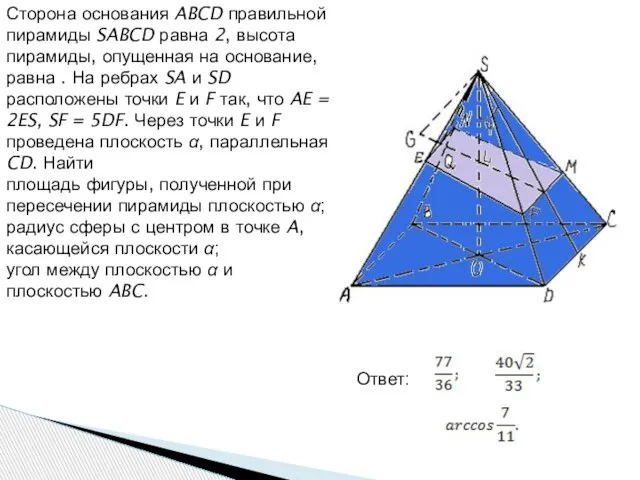
Сторона основания ABCD правильной пирамиды SABCD равна 2, высота пирамиды, опущенная на основание, равна . На ребрах SA и SD расположены точки E и F так, что AE = 2ES, SF = 5DF. Через точки E и F проведена плоскость α, параллельная CD. Найти
площадь фигуры, полученной при пересечении пирамиды плоскостью α;
радиус сферы с центром в точке A, касающейся плоскости α;
угол между плоскостью α и плоскостью ABC.
Ответ:

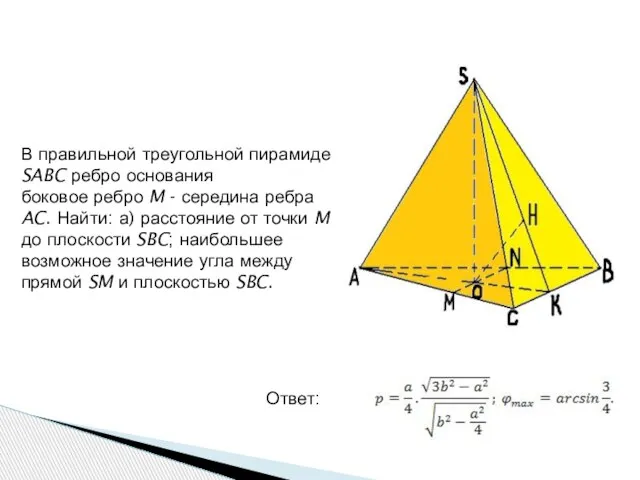
В правильной треугольной пирамиде SABC ребро основания
боковое ребро M - середина ребра AC. Найти: а) расстояние от точки M до плоскости SBC; наибольшее возможное значение угла между прямой SM и плоскостью SBC.
Ответ:

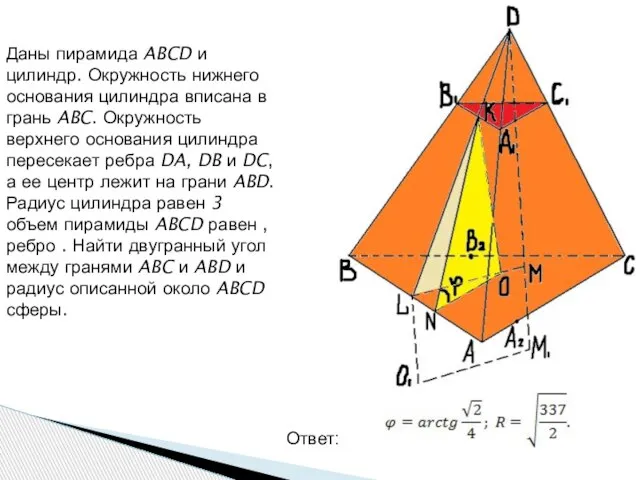
Даны пирамида ABCD и цилиндр. Окружность нижнего основания цилиндра вписана в грань ABC. Окружность верхнего основания цилиндра пересекает ребра DA, DB и DC, а ее центр лежит на грани ABD. Радиус цилиндра равен 3 объем пирамиды ABCD равен , ребро . Найти двугранный угол между гранями ABC и ABD и радиус описанной около ABCD сферы.
Ответ:

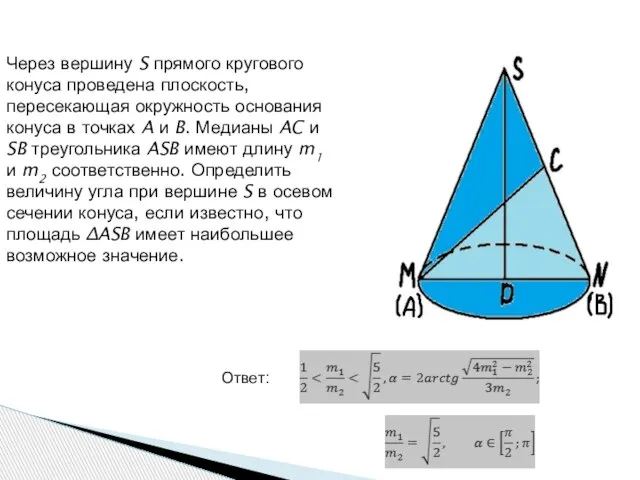
Через вершину S прямого кругового конуса проведена плоскость, пересекающая окружность основания конуса в точках A и B. Медианы AC и SB треугольника ASB имеют длину m1 и m2 соответственно. Определить величину угла при вершине S в осевом сечении конуса, если известно, что площадь ∆ASB имеет наибольшее возможное значение.
Ответ:

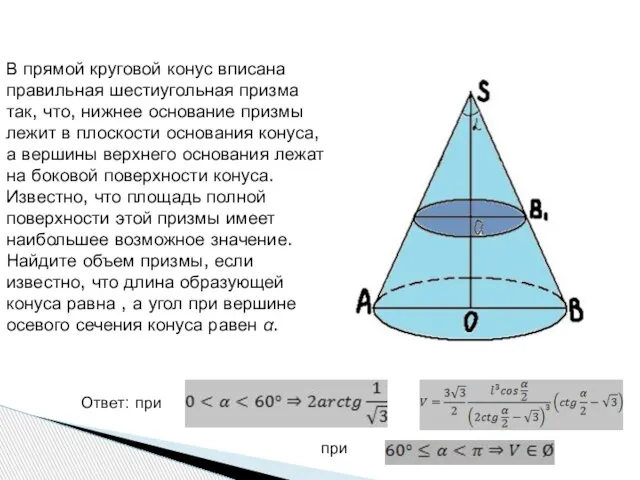
В прямой круговой конус вписана правильная шестиугольная призма так, что, нижнее основание призмы лежит в плоскости основания конуса, а вершины верхнего основания лежат на боковой поверхности конуса. Известно, что площадь полной поверхности этой призмы имеет наибольшее возможное значение. Найдите объем призмы, если известно, что длина образующей конуса равна , а угол при вершине осевого сечения конуса равен α.
Ответ: при
при

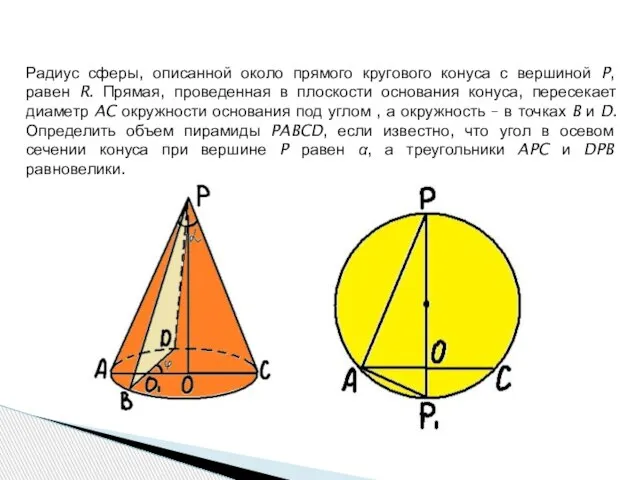
Радиус сферы, описанной около прямого кругового конуса с вершиной P, равен R. Прямая, проведенная в плоскости основания конуса, пересекает диаметр AC окружности основания под углом , а окружность – в точках B и D. Определить объем пирамиды PABCD, если известно, что угол в осевом сечении конуса при вершине P равен α, а треугольники APC и DPB равновелики.

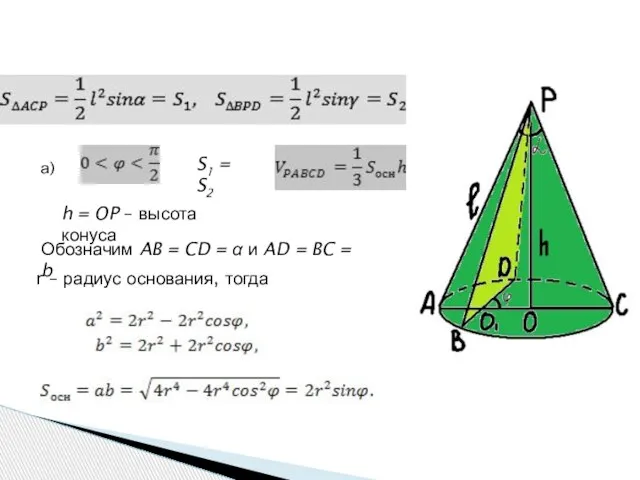
а)
S1 = S2
h = OP – высота конуса
Обозначим AB = CD = α и AD = BC = b
r – радиус основания, тогда

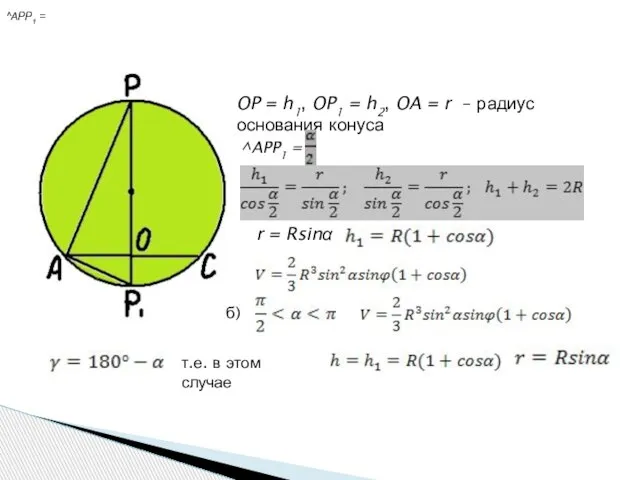
OP = h1, OP1 = h2, OA = r – радиус основания конуса
^APP1 =
^APP1 =
r = Rsinα
,
б)
т.е. в этом случае