Задачи оптимизации

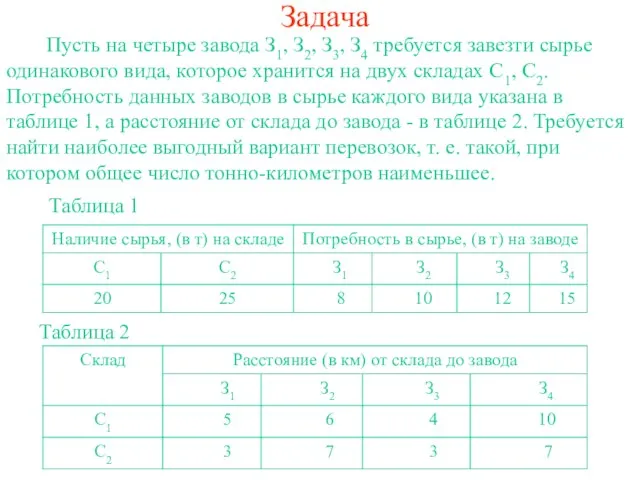
Задача
Пусть на четыре завода З1, З2, З3, З4 требуется завезти сырье одинакового вида, которое хранится на двух складах С1, С2. Потребность данных заводов в сырье каждого вида указана в таблице 1, а расстояние от склада до завода - в таблице 2. Требуется найти наиболее выгодный вариант перевозок, т. е. такой, при котором общее число тонно-километров наименьшее.
Таблица 1
Таблица 2

Решение
Для решения этой задачи, в первую очередь, проанализируем ее условие и переведем его на язык математики, т. е. составим математическую модель. Для этого количество сырья, которое нужно перевезти со склада С1 на заводы З1, З2, З3, обозначим через x, y и z соответственно. Тогда на четвертый завод с этого склада нужно будет перевезти 20 - x – y - z сырья в тоннах, а со второго склада нужно будет перевезти соответственно 8 - x, 10 - y, 12 - z, x + y + z - 5 сырья в тоннах. Запишем эти данные в таблицу 3.
Таблица 3

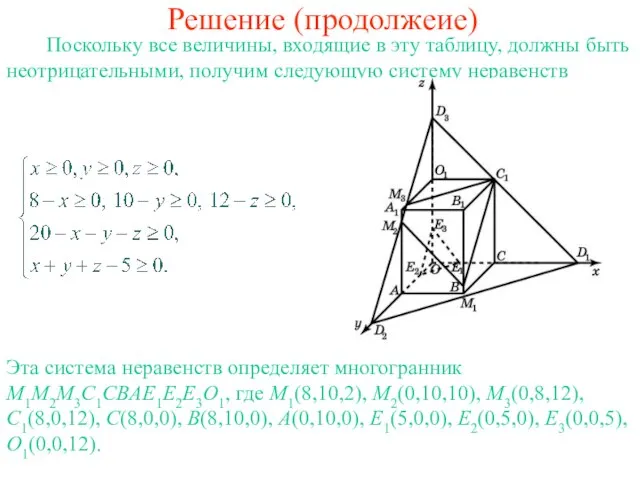
Решение (продолжеие)
Поскольку все величины, входящие в эту таблицу, должны быть неотрицательными, получим следующую систему неравенств
Эта система неравенств определяет многогранник M1M2M3C1CBAE1E2E3O1, где M1(8,10,2), M2(0,10,10), M3(0,8,12), C1(8,0,12), C(8,0,0), B(8,10,0), A(0,10,0), E1(5,0,0), E2(0,5,0), E3(0,0,5), O1(0,0,12).

Решение (продолжение)
Общее число тонно-километров выражается формулой: 5x + 6y + 4z + 10(20 - x - y - z) + 3(8 - x) + 7(10 - y) + 3(12 - z) + 7(x + y + z - 5) = 295 - x - 4y - 2z.
Таким образом, задача сводится к отысканию наименьшего значения функции F = 295 - x - 4y - 2z на многограннике ограничений. Для этого достаточно найти наибольшее значение функции f = x + 4y + 2z. Тогда Fmin = 295 - fmax.
Для нахождения наибольшего значения линейной функции на многограннике, достаточно вычислить значения функции в вершинах многогранника и выбрать из них наибольшее. Вычислим значение функции f = x + 4y + 2z в вершинах многогранника ограниче­ний: f(M1) = 52, f(M2) = 60, f(M3) = 56, f(C1) = 32, f(C) = 8, f(B) = 48, f(A) = 40, f(E1) = 5, f(E2) = 20, f(E3) = 10, f(O1) = 24. Легко видеть, что максимальное значение функции f равно 60. Тогда Fmin = 295 - 60 = 235. Это значение функция F принимает в точке M2(0,10,10).

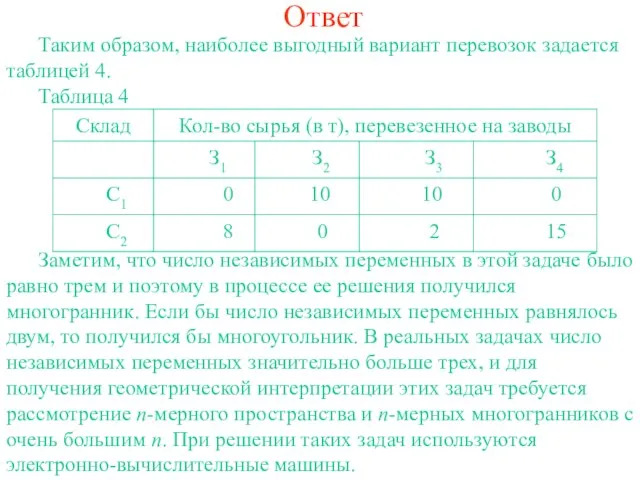
Ответ
Таким образом, наиболее выгодный вариант перевозок задается таблицей 4.
Таблица 4
Заметим, что число независимых переменных в этой задаче было равно трем и поэтому в процессе ее решения получился многогранник. Если бы число независимых переменных равнялось двум, то получился бы многоугольник. В реальных задачах число независимых переменных значительно больше трех, и для получения геометрической интерпретации этих задач требуется рассмотрение n-мерного пространства и n-мерных многогранников с очень большим n. При решении таких задач используются электронно-вычислительные машины.

Упражнение 1
Какая фигура является графиком линейной функции z = ax + by + c?
Ответ: Плоскость.

Упражнение 2
Как расположен график линейной функции z = ax + c по отношению к оси Oy?
Ответ: Параллелен.

Упражнение 3
Как расположен график линейной функции z = ax + by по отношению к началу координат?
Ответ: Проходит через начало координат.

Упражнение 4
Что произойдет с графиком линейной функции z = ax + by + c, если c: а) увеличить на единицу; б) уменьшить на единицу?
Ответ: а) Поднимется на единицу;
б) опустится на единицу.

Упражнение 5
Пусть математическая модель некоторой задачи представляется следующей системой ограничений
Ответ: -2.
На множестве решений этой системы найдите наименьшее значение функции F = y - x.

Упражнение 6
На трех складах хранится сырье одинакового вида в количествах соответственно 10 т, 20 т, 30 т. На завод нужно завезти 35 т сырья. Найдите наиболее выгодный вариант перевозок, если расстояния от складов до завода равны 7 км, 5 км, 8 км.
Ответ: С 1-го склада – 10 т, со 2-го – 20 т, с 3-го – 5 т.

Упражнение 7
Решите предыдущую задачу при дополнительном требовании: со второго склада вывозится сырья не больше, чем с третьего.
Ответ: С 1-го склада – 0 т, со 2-го и 3-го – 17,5 т.