Содержание
- 2. 10. Развёртки поверхностей Развертка поверхности – фигура, полученная при совмещении развертываемой поверхности с плоскостью без разрывов
- 3. 10. Развёртки поверхностей Для развёртываемых поверхностей (гранных, цилиндрических, конических) выполняют: точные развёртки (например, развёртки многогранников); приближённые
- 4. Развертки боковой поверхности прямых круговых цилиндра (рис. 69) и конуса (рис. 70)
- 5. В общем случае: цилиндрическую поверхность можно приближенно развернуть, заменив её вписанной или описанной призмой. коническую поверхность
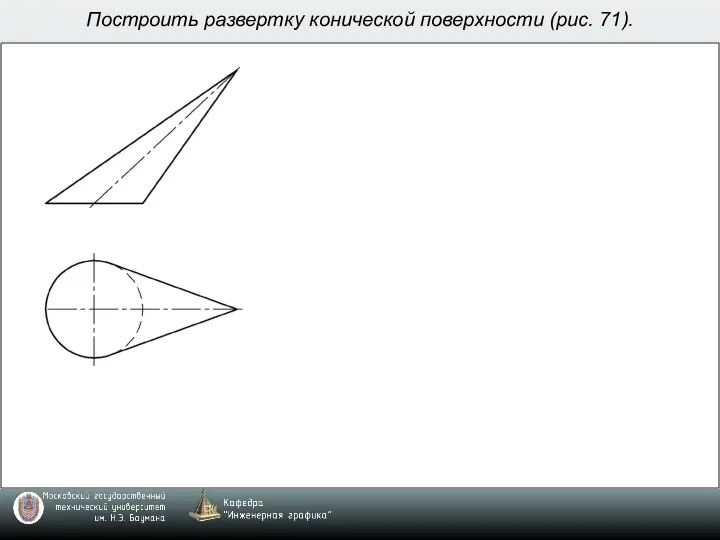
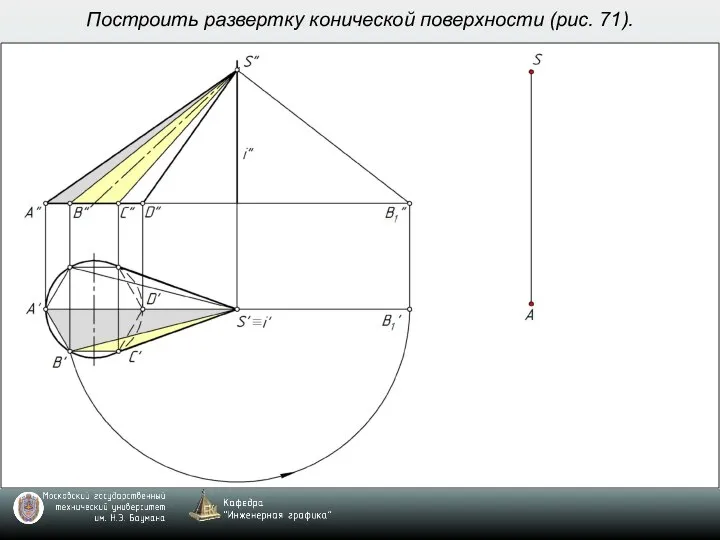
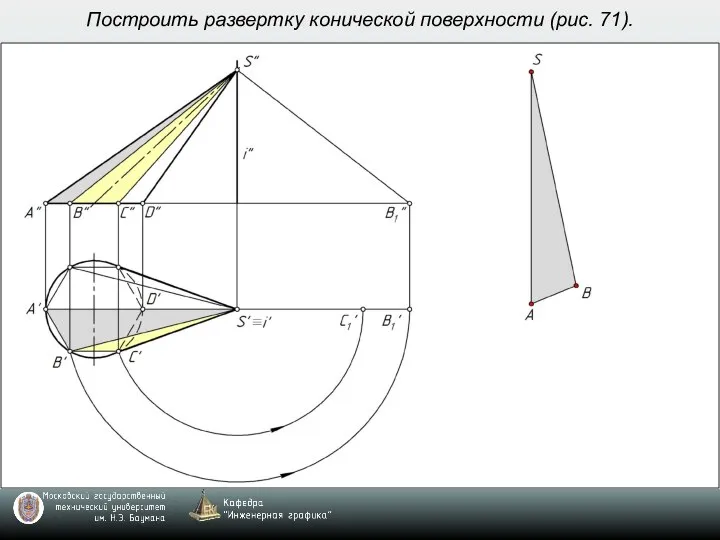
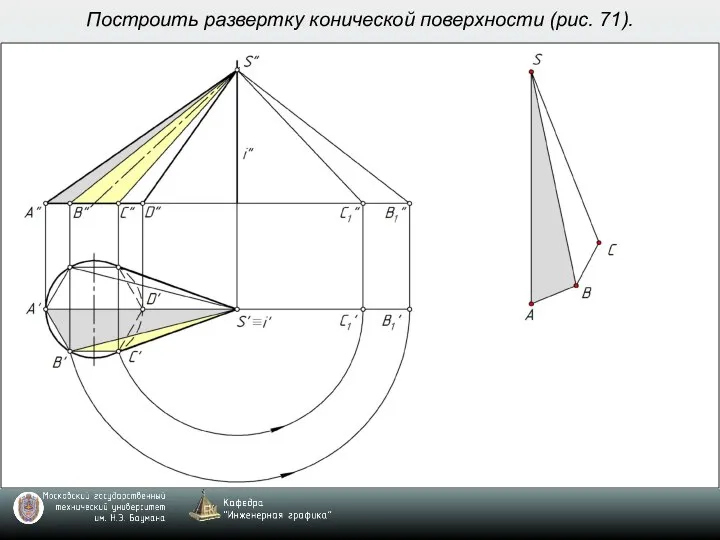
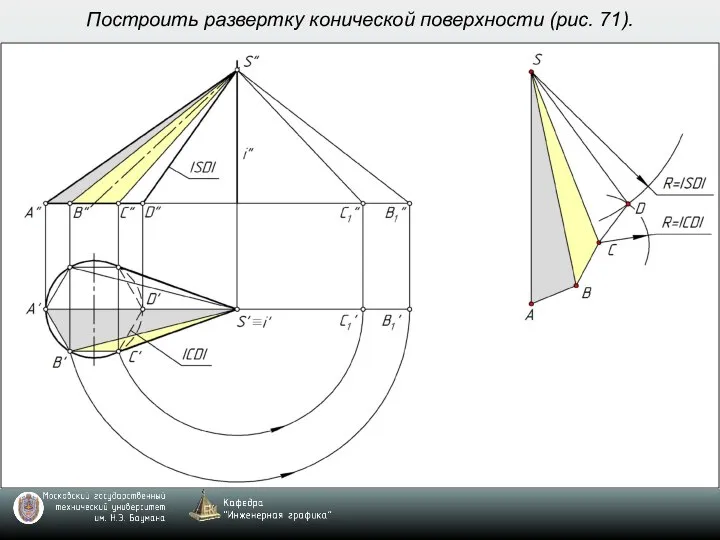
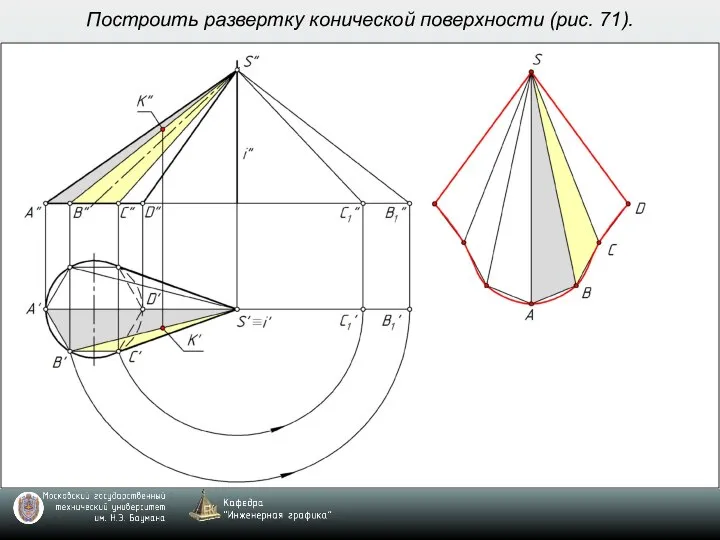
- 6. Построить развертку конической поверхности (рис. 71).
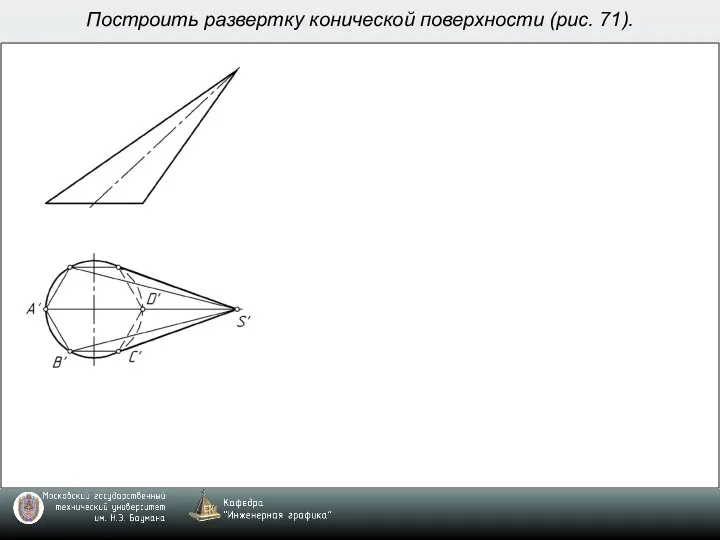
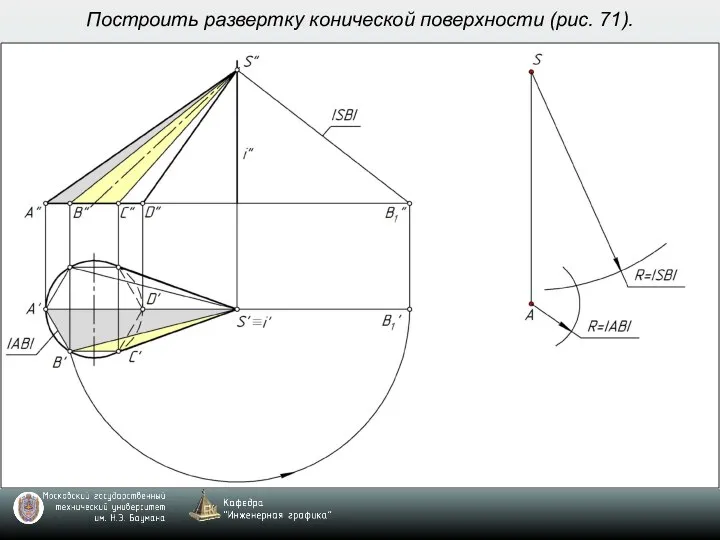
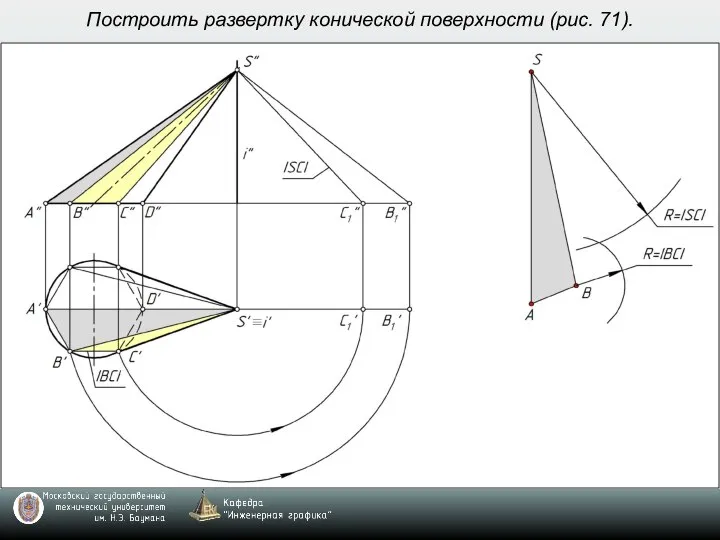
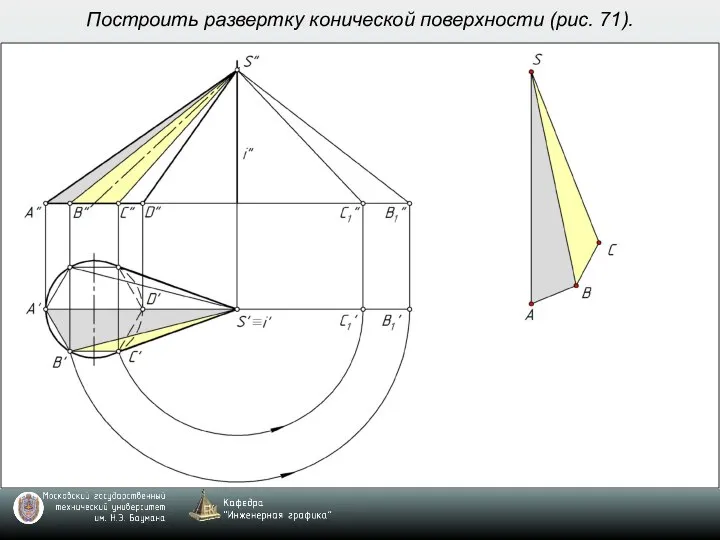
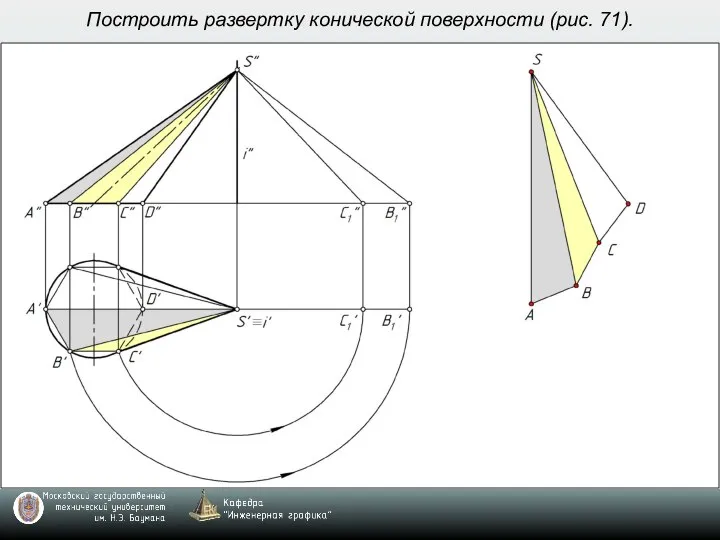
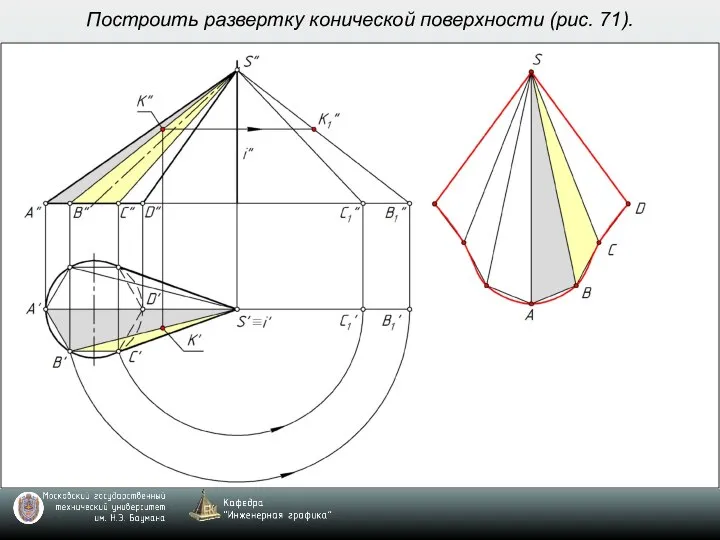
- 7. Построить развертку конической поверхности (рис. 71).
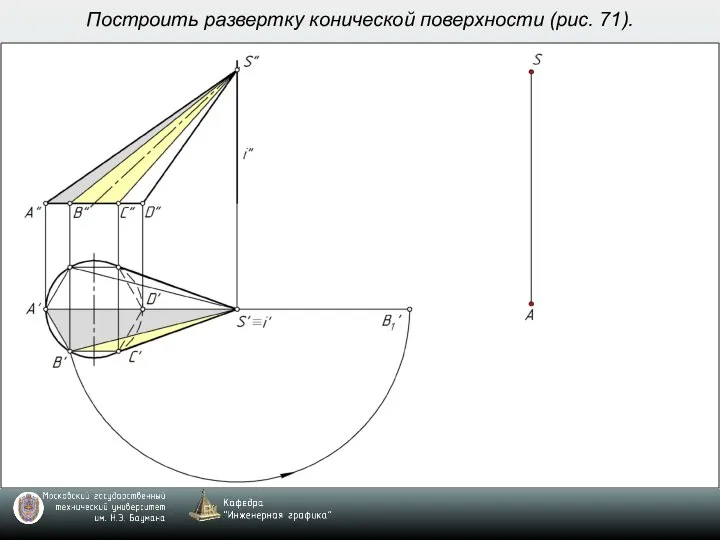
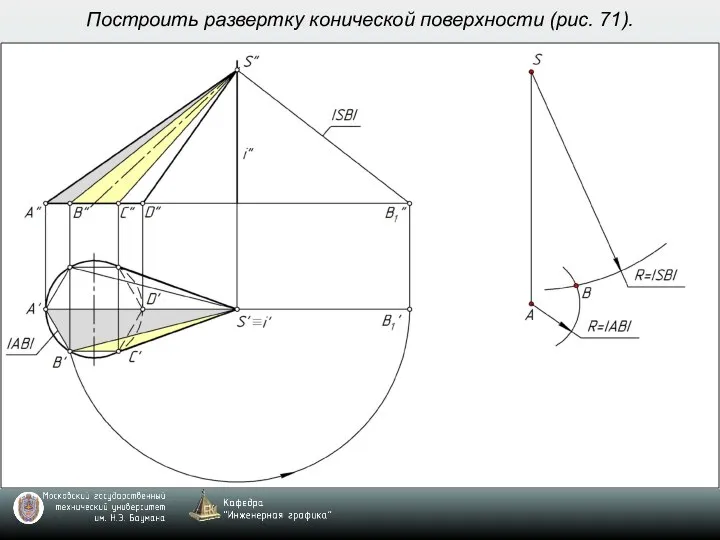
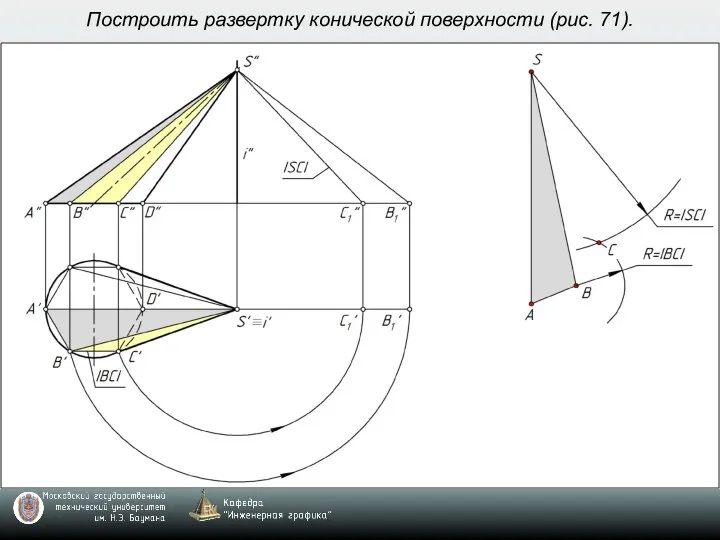
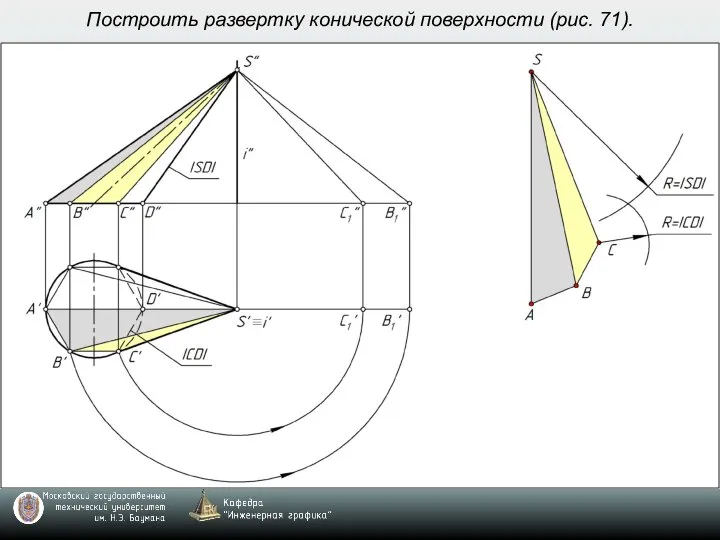
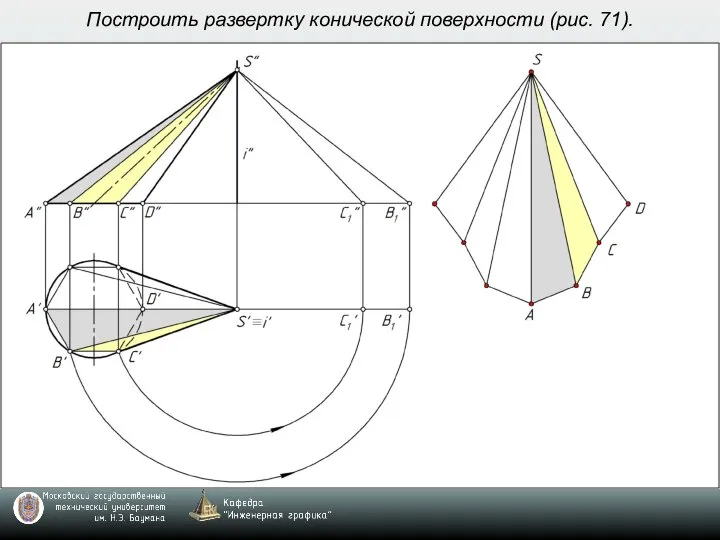
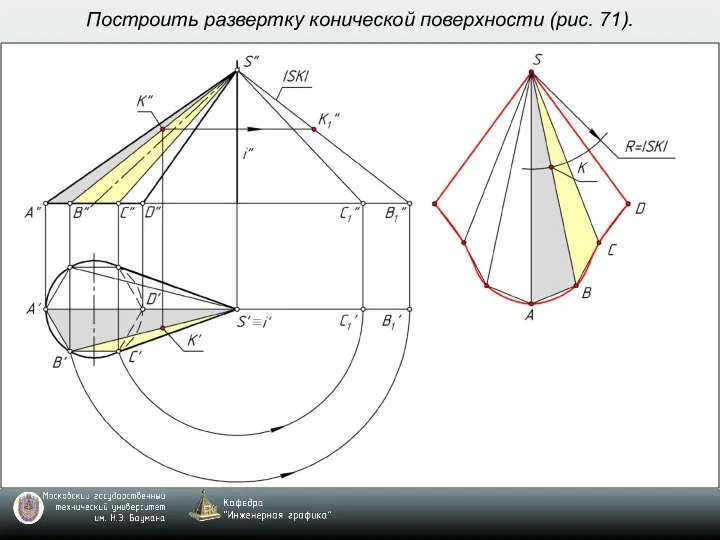
- 8. Построить развертку конической поверхности (рис. 71).
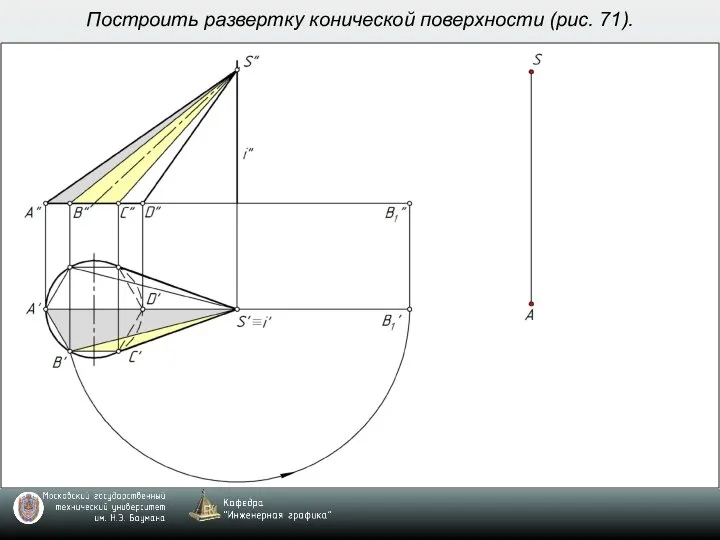
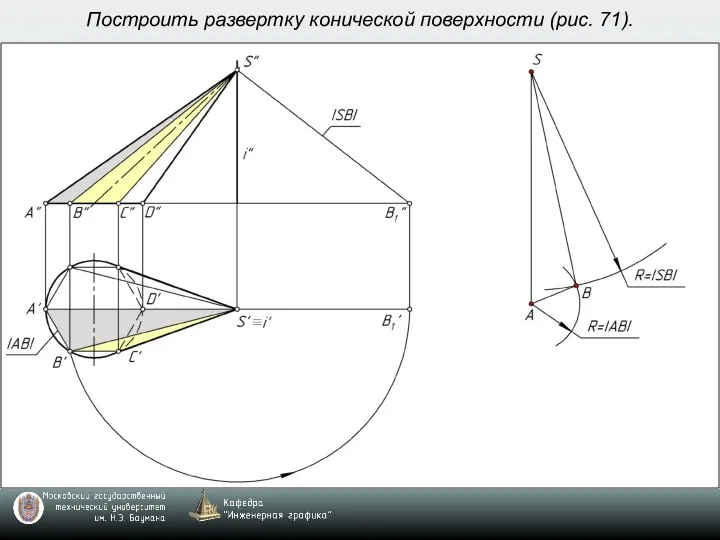
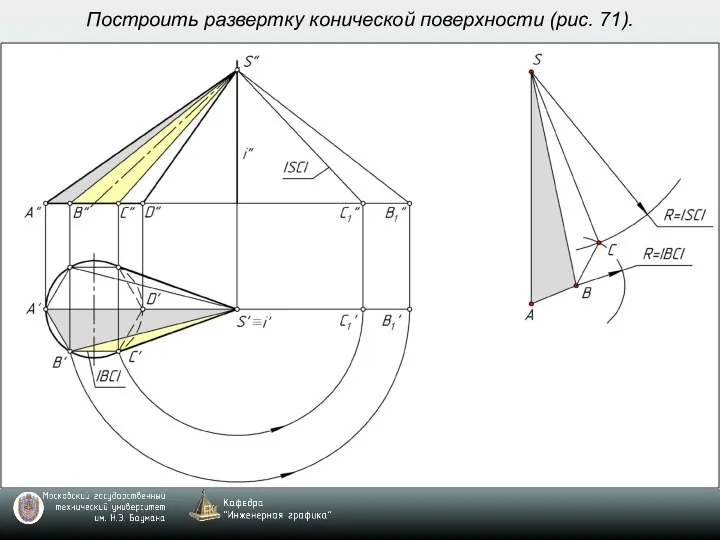
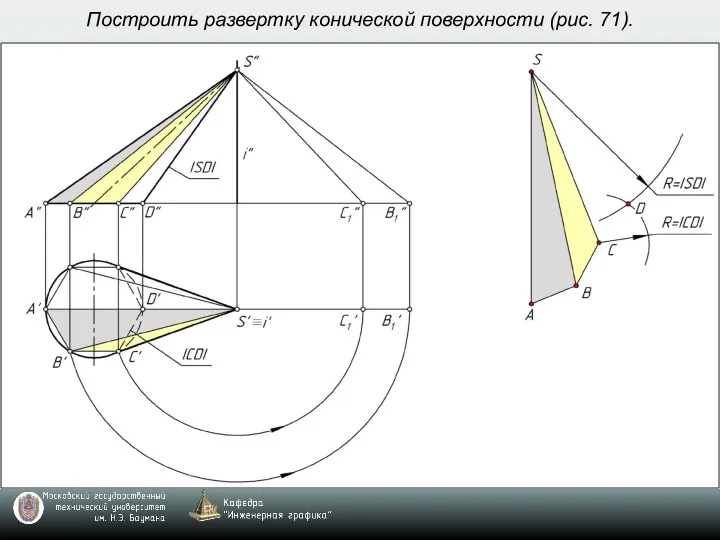
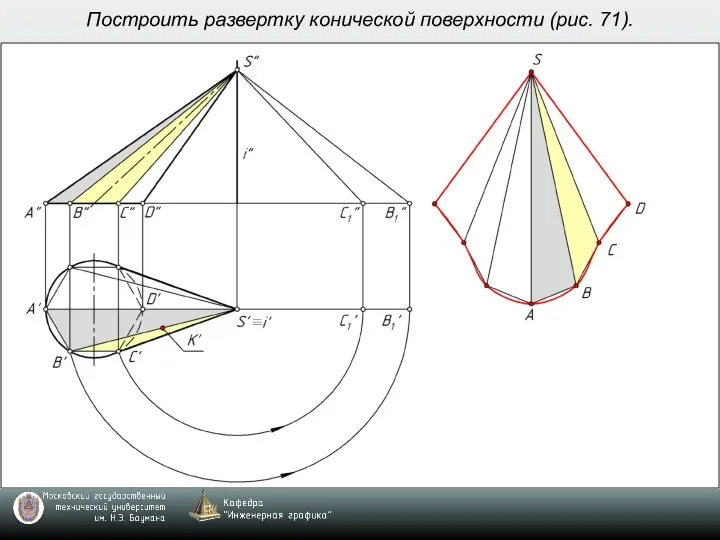
- 9. Построить развертку конической поверхности (рис. 71).
- 10. Построить развертку конической поверхности (рис. 71).
- 11. Построить развертку конической поверхности (рис. 71).
- 12. Построить развертку конической поверхности (рис. 71).
- 13. Построить развертку конической поверхности (рис. 71).
- 14. Построить развертку конической поверхности (рис. 71).
- 15. Построить развертку конической поверхности (рис. 71).
- 16. Построить развертку конической поверхности (рис. 71).
- 17. Построить развертку конической поверхности (рис. 71).
- 18. Построить развертку конической поверхности (рис. 71).
- 19. Построить развертку конической поверхности (рис. 71).
- 20. Построить развертку конической поверхности (рис. 71).
- 21. Построить развертку конической поверхности (рис. 71).
- 22. Построить развертку конической поверхности (рис. 71).
- 23. Построить развертку конической поверхности (рис. 71).
- 24. Построить развертку конической поверхности (рис. 71).
- 25. Построить развертку конической поверхности (рис. 71).
- 26. Построить развертку конической поверхности (рис. 71).
- 27. Построить развертку конической поверхности (рис. 71).
- 28. Построить развертку конической поверхности (рис. 71).
- 29. Построить развертку конической поверхности (рис. 71).
- 30. Построить развертку конической поверхности (рис. 71).
- 31. Построить развертку конической поверхности (рис. 71).
- 32. Построить развертку конической поверхности (рис. 71).
- 33. Построить развертку конической поверхности (рис. 71).
- 34. Построить развертку конической поверхности (рис. 71).
- 35. Построить развертку конической поверхности (рис. 71).
- 36. Построить развертку конической поверхности (рис. 71).
- 37. Построить развертку конической поверхности (рис. 71).
- 38. Построить развертку конической поверхности (рис. 71).
- 39. Построить развертку конической поверхности (рис. 71).
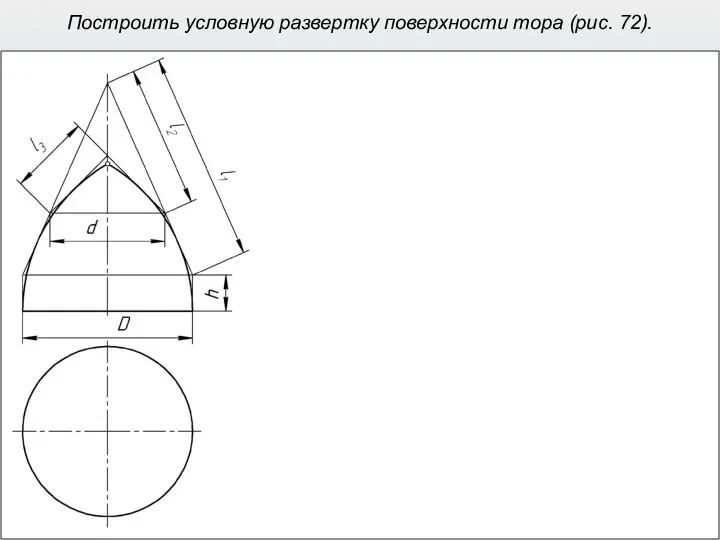
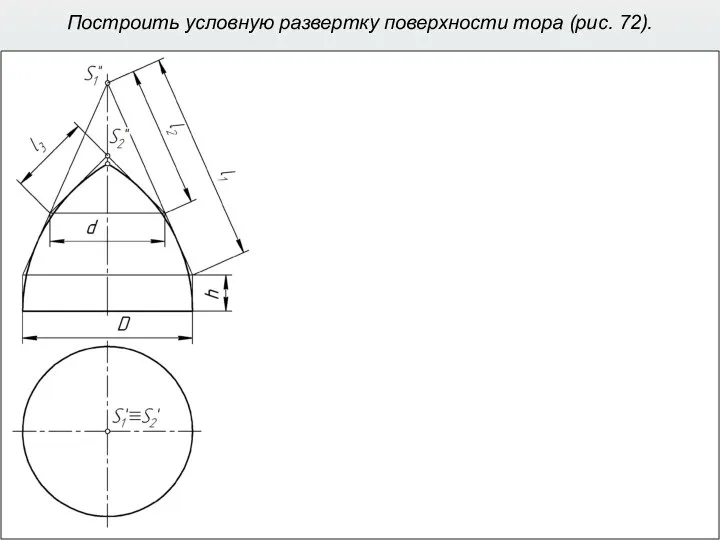
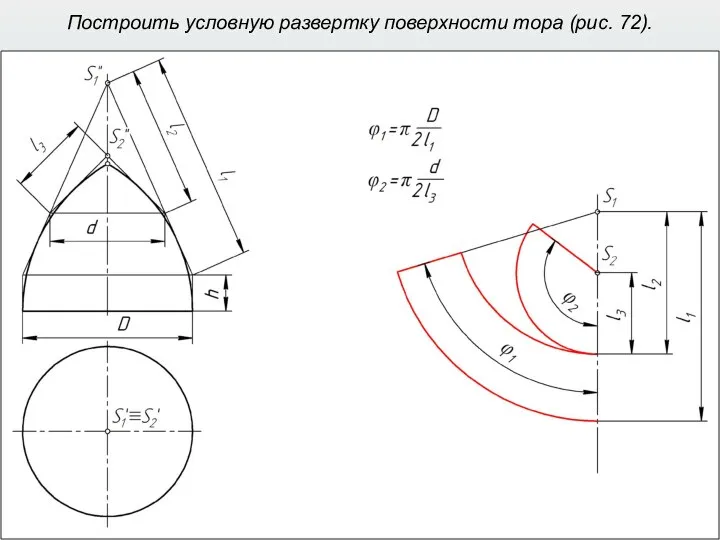
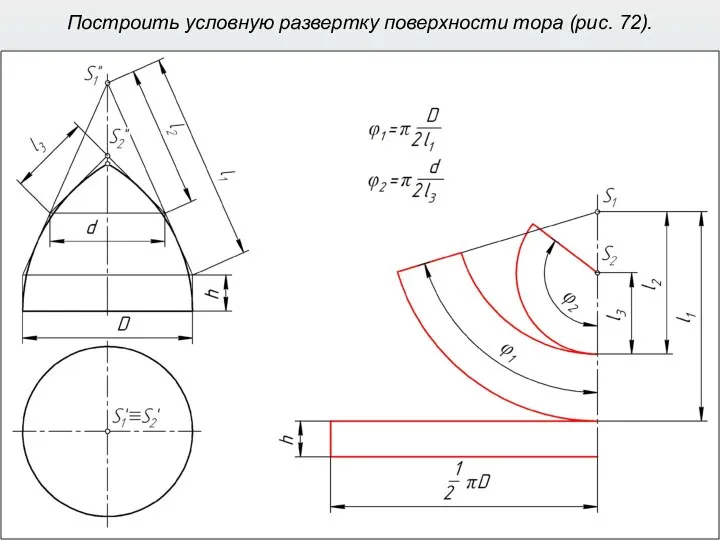
- 40. Построить условную развертку поверхности тора (рис. 72).
- 41. Построить условную развертку поверхности тора (рис. 72).
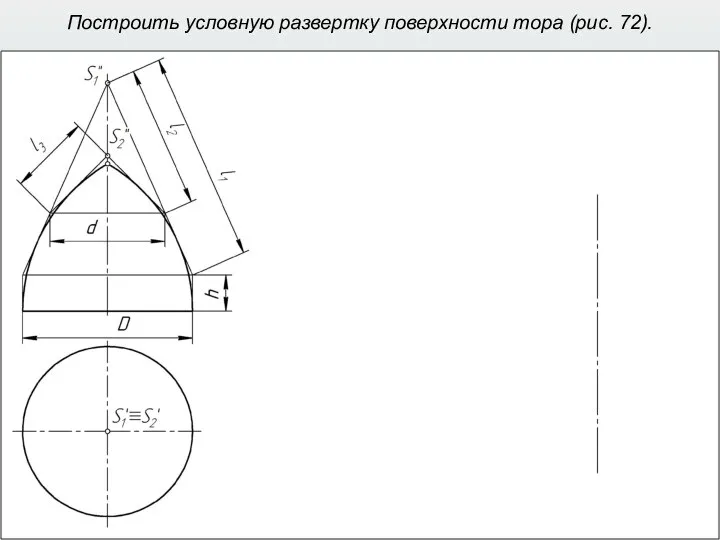
- 42. Построить условную развертку поверхности тора (рис. 72).
- 43. Построить условную развертку поверхности тора (рис. 72).
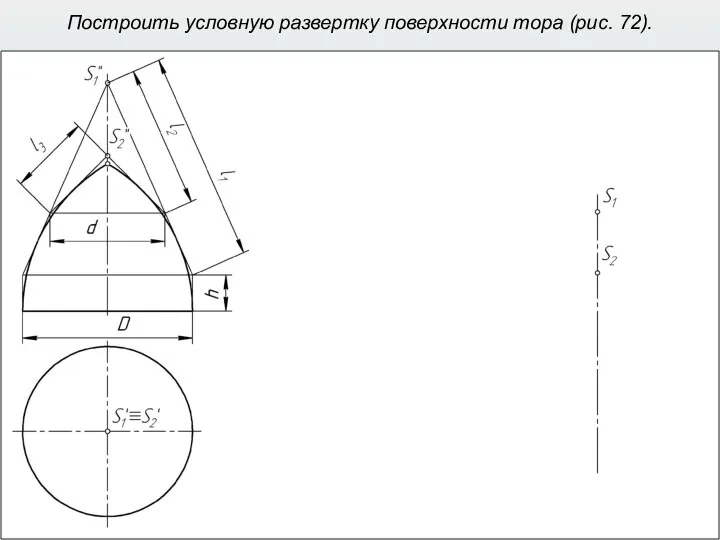
- 44. Построить условную развертку поверхности тора (рис. 72).
- 45. Построить условную развертку поверхности тора (рис. 72).
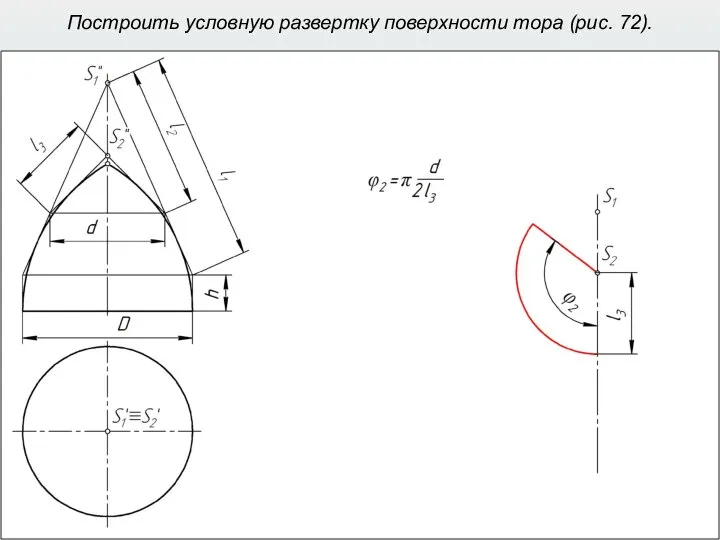
- 46. Построить условную развертку поверхности тора (рис. 72).
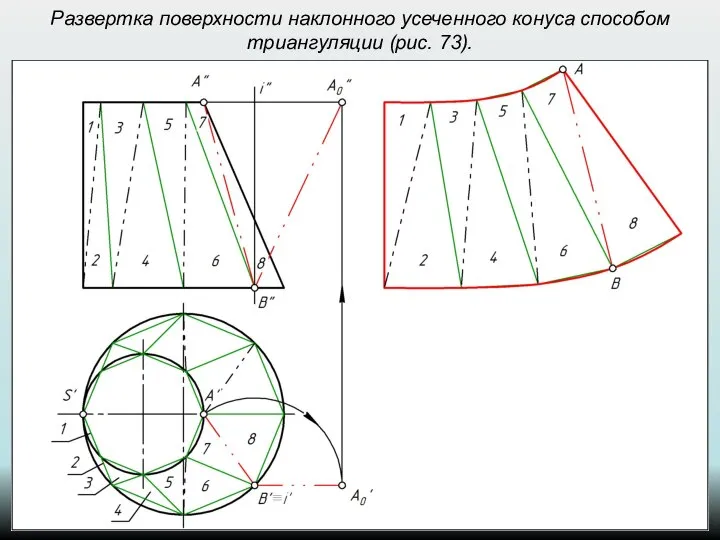
- 47. Развертка поверхности наклонного усеченного конуса способом триангуляции (рис. 73).
- 48. 11. Аксонометрические проекции Аксонометрия позволяет с использованием способа двух изображений получить наглядное изображение фигуры (предмета). Для
- 49. Основная теорема аксонометрии (теорема К. Польке 1851г.) Три отрезка прямых произвольной длины, лежащих в одной плоскости
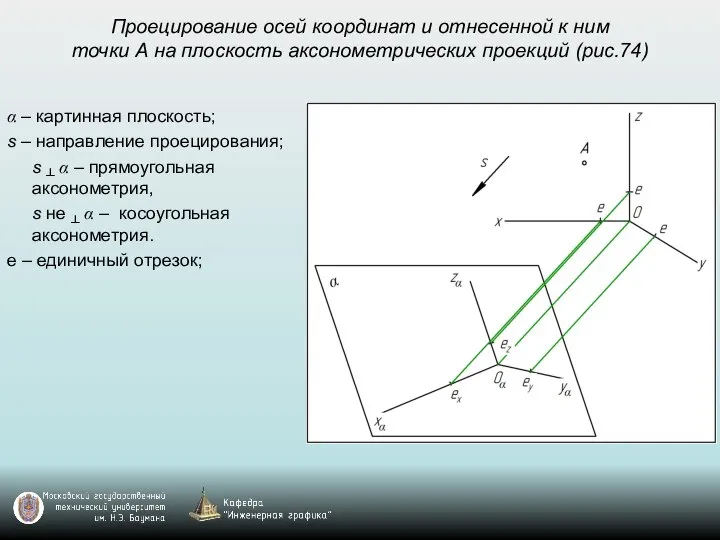
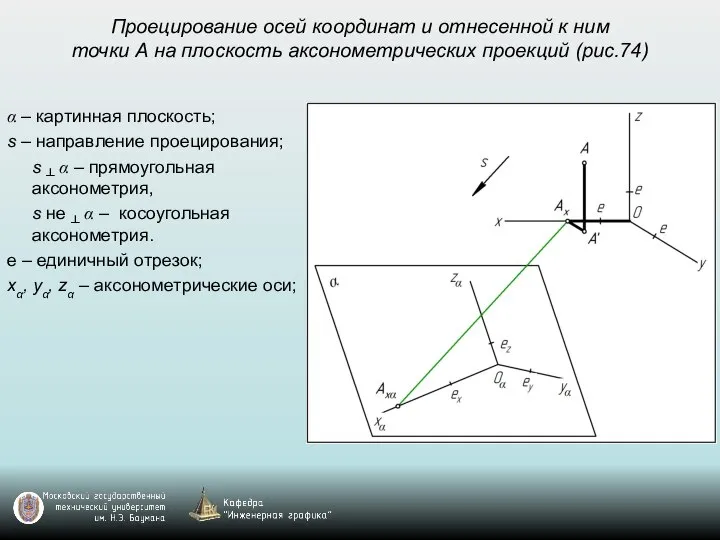
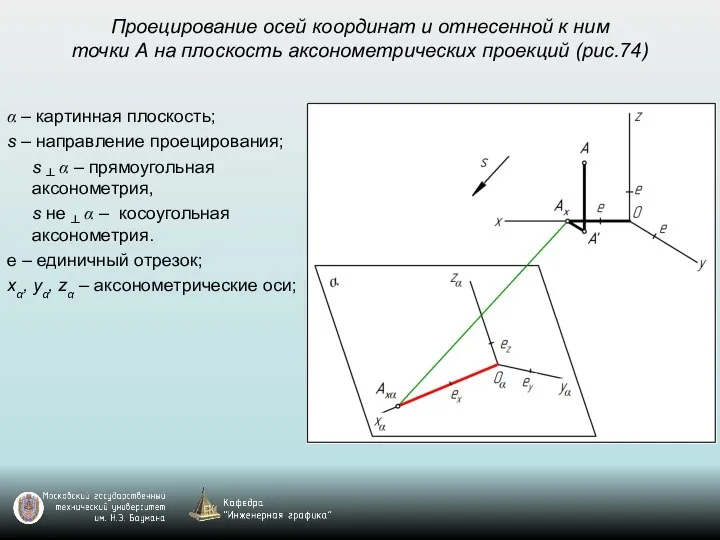
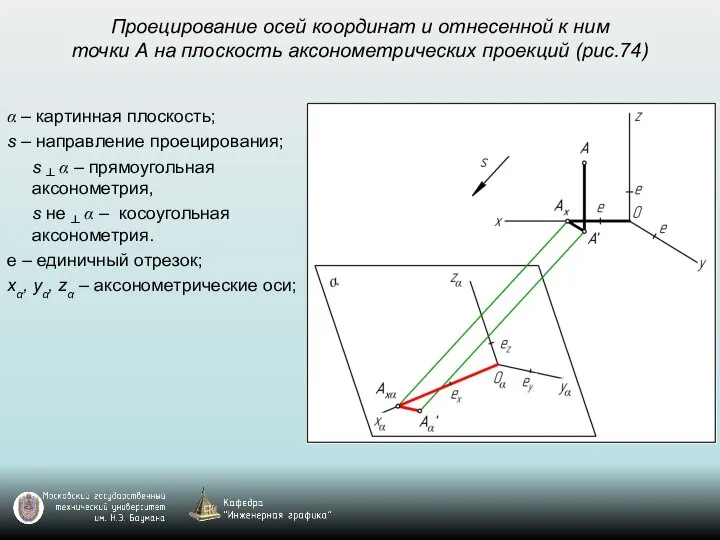
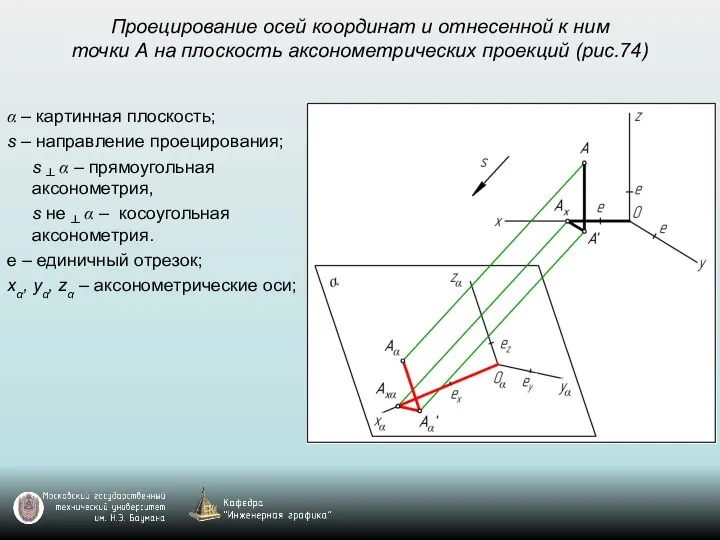
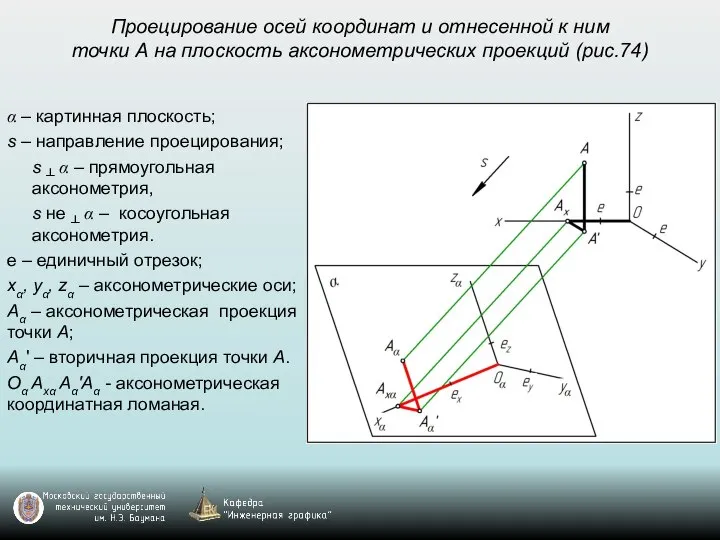
- 50. Проецирование осей координат и отнесенной к ним точки А на плоскость аксонометрических проекций (рис.74) α –
- 51. Проецирование осей координат и отнесенной к ним точки А на плоскость аксонометрических проекций (рис.74) α –
- 52. Проецирование осей координат и отнесенной к ним точки А на плоскость аксонометрических проекций (рис.74) α –
- 53. Проецирование осей координат и отнесенной к ним точки А на плоскость аксонометрических проекций (рис.74) α –
- 54. Проецирование осей координат и отнесенной к ним точки А на плоскость аксонометрических проекций (рис.74) α –
- 55. Проецирование осей координат и отнесенной к ним точки А на плоскость аксонометрических проекций (рис.74) α –
- 56. Проецирование осей координат и отнесенной к ним точки А на плоскость аксонометрических проекций (рис.74) α –
- 57. Проецирование осей координат и отнесенной к ним точки А на плоскость аксонометрических проекций (рис.74) α –
- 58. Проецирование осей координат и отнесенной к ним точки А на плоскость аксонометрических проекций (рис.74) α –
- 59. Проецирование осей координат и отнесенной к ним точки А на плоскость аксонометрических проекций (рис.74) α –
- 60. Проецирование осей координат и отнесенной к ним точки А на плоскость аксонометрических проекций (рис.74) α –
- 61. В общем случае еx ≠ еy≠ еz ≠ е k, m, n - коэффициенты (или показатели)
- 62. Теорема К. Польке справедлива для косоугольной аксонометрии и недействительна для прямоугольной аксонометрии. Выбор аксонометрической системы координат
- 63. Прямоугольные аксонометрические проекции k2 + m2 + n2 = 2 [Иванов Г.С. Начертательная геометрия: учебник. –
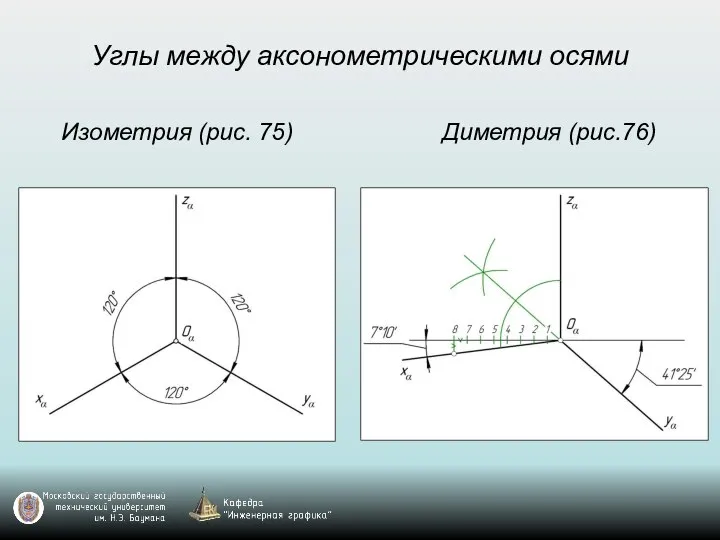
- 64. Углы между аксонометрическими осями Изометрия (рис. 75) Диметрия (рис.76)
- 65. Построение аксонометрических проекций окружностей, расположенных в координатных плоскостях xy, xz, yz или в плоскостях, им параллельных
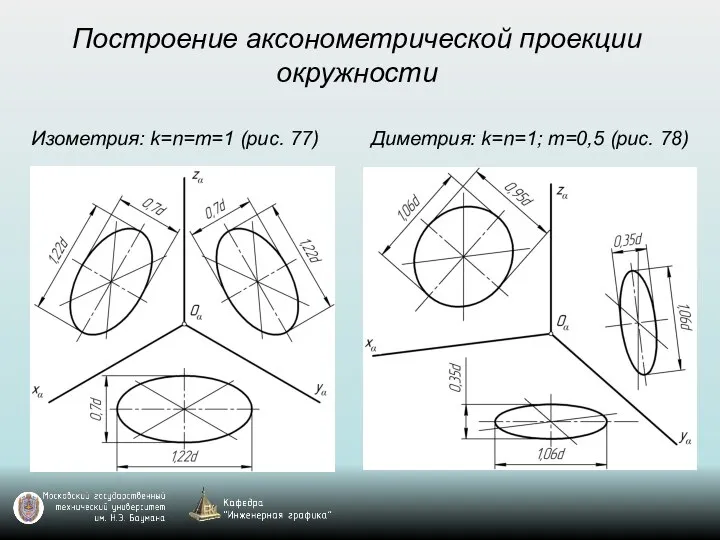
- 66. Построение аксонометрической проекции окружности Изометрия: k=n=m=1 (рис. 77) Диметрия: k=n=1; m=0,5 (рис. 78)
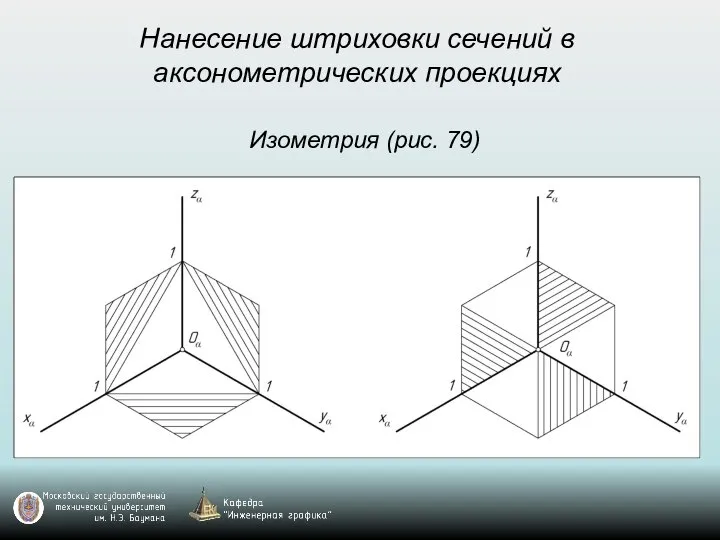
- 67. Нанесение штриховки сечений в аксонометрических проекциях Изометрия (рис. 79)
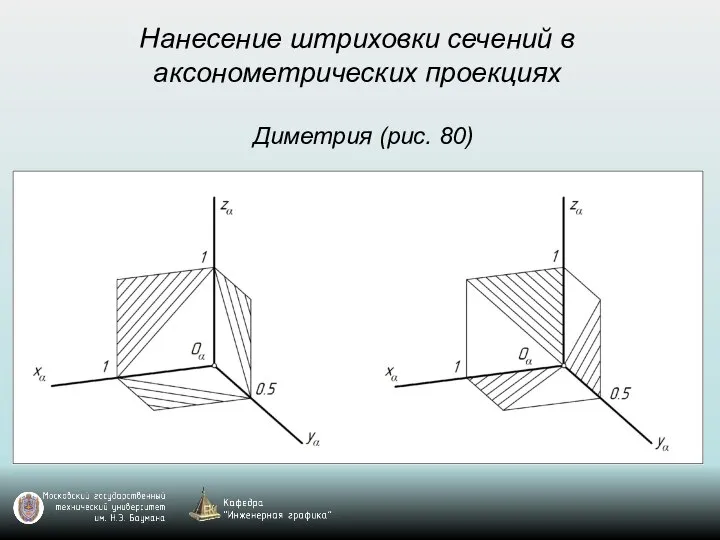
- 68. Нанесение штриховки сечений в аксонометрических проекциях Диметрия (рис. 80)
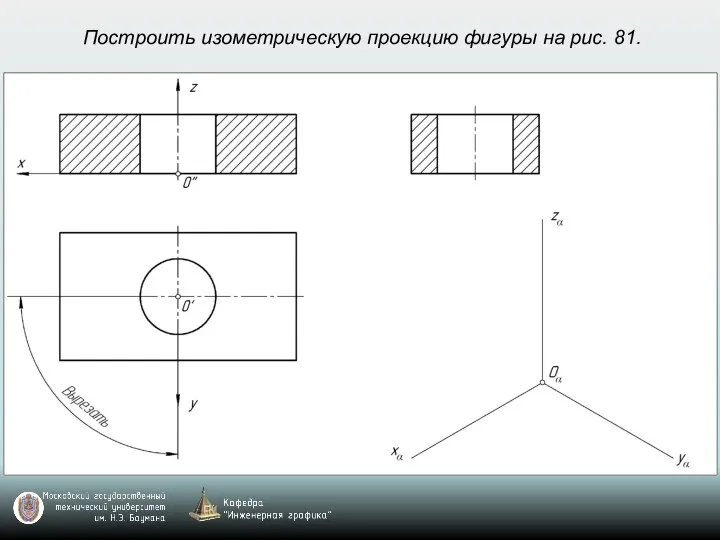
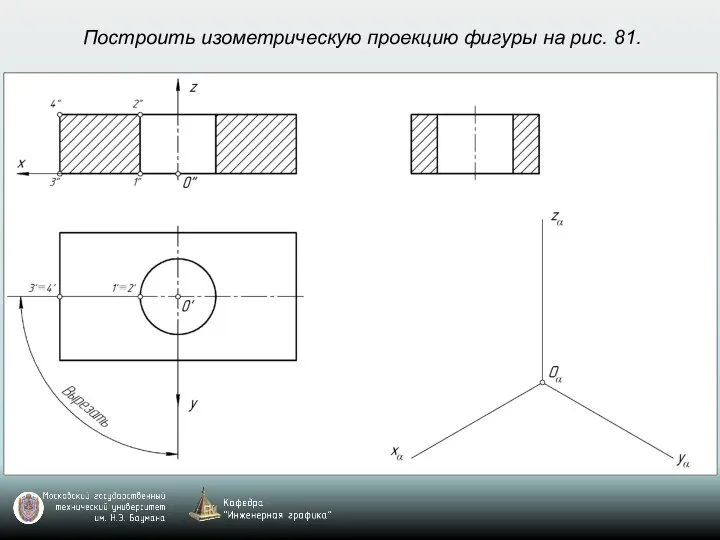
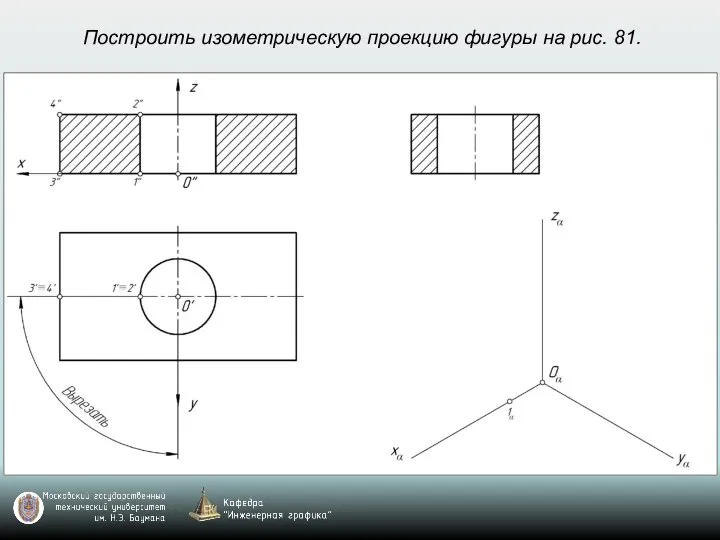
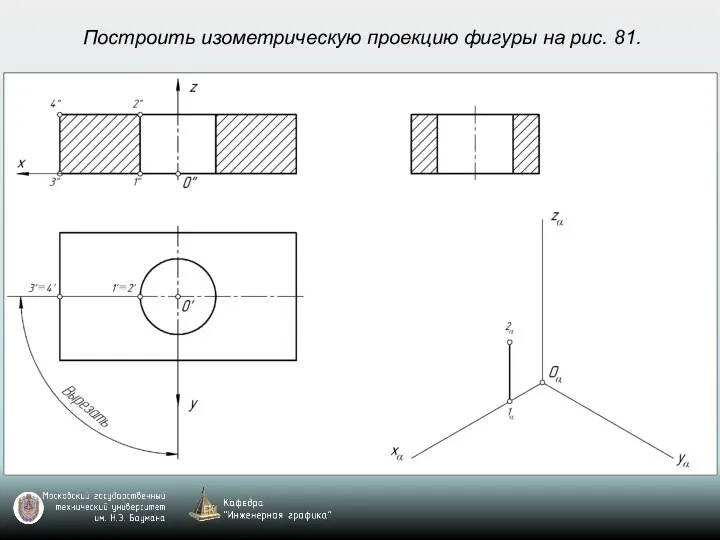
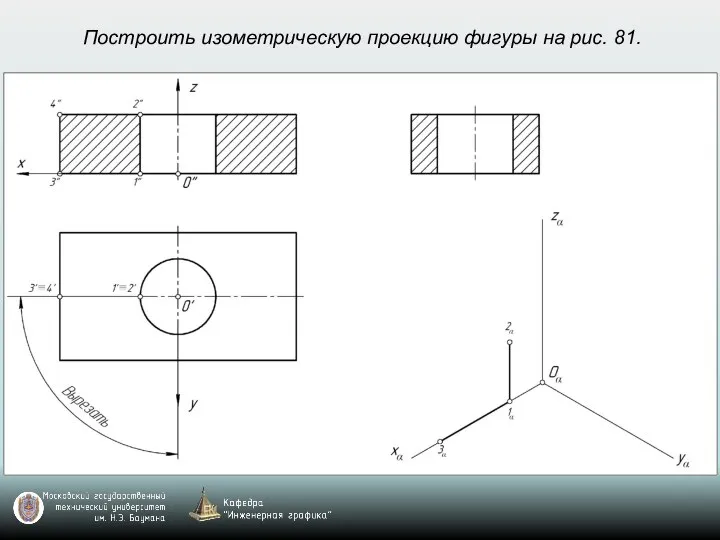
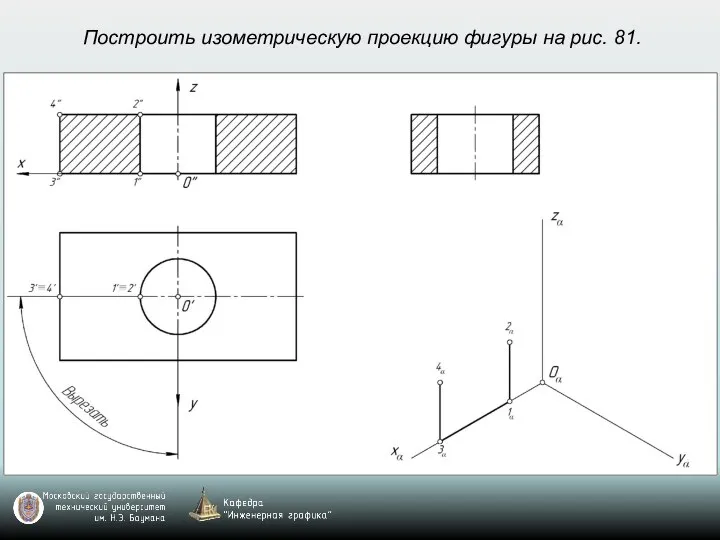
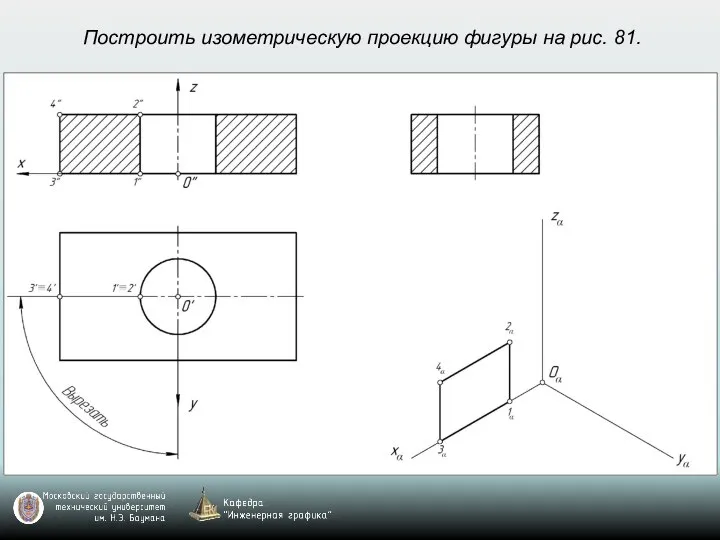
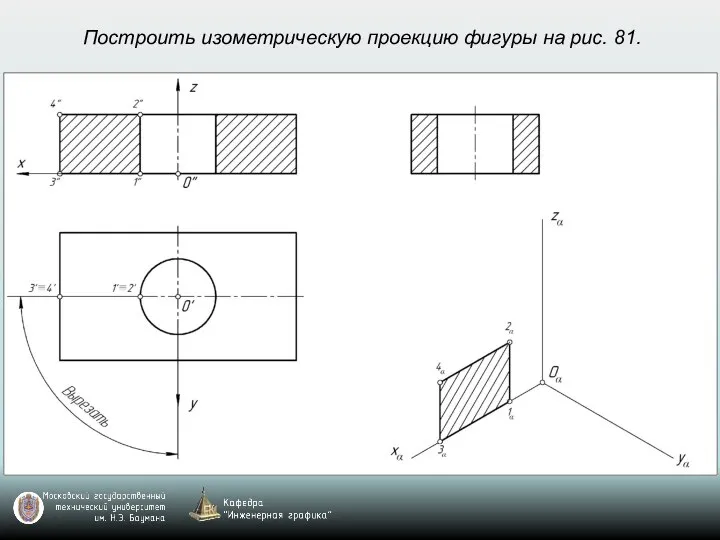
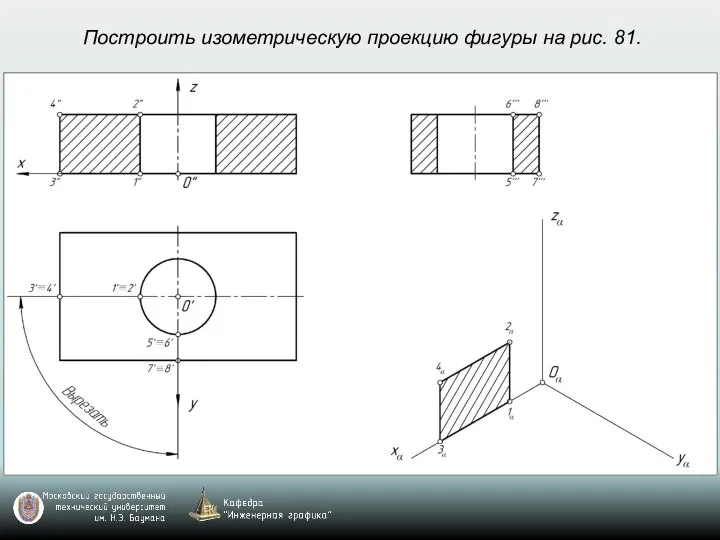
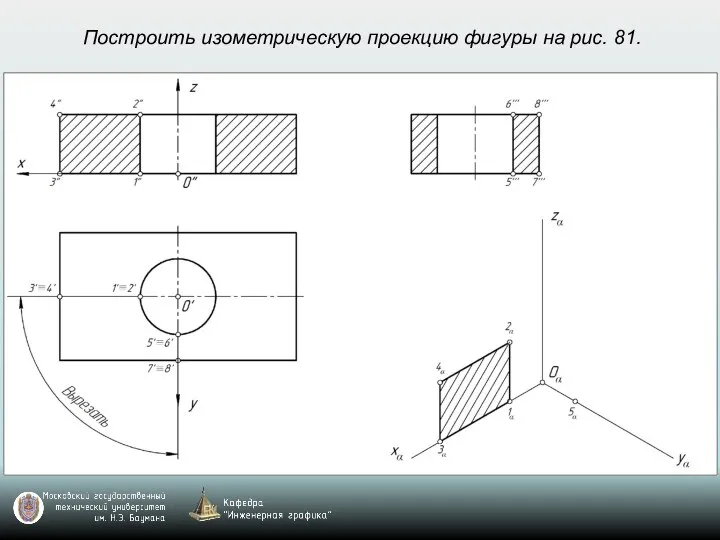
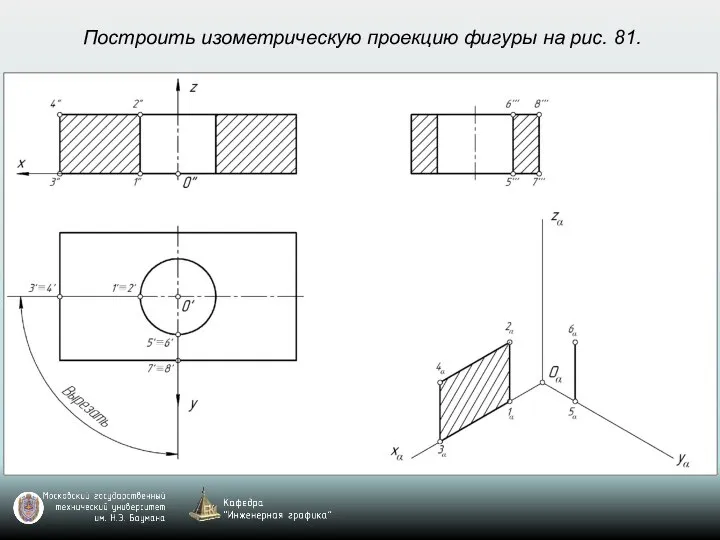
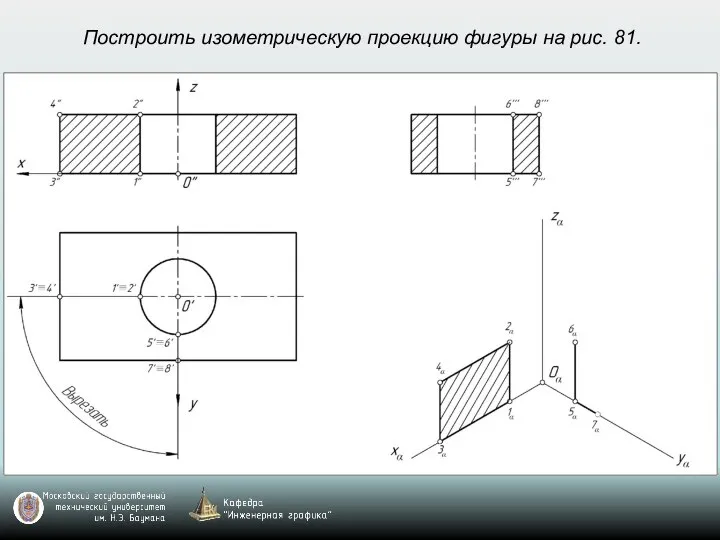
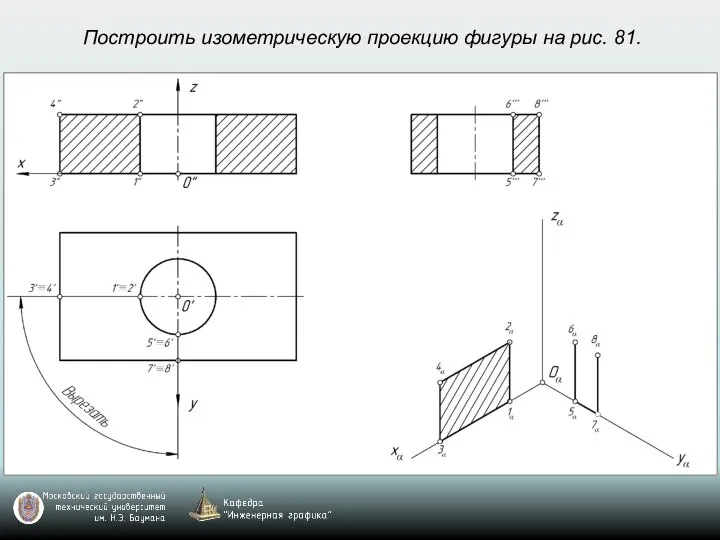
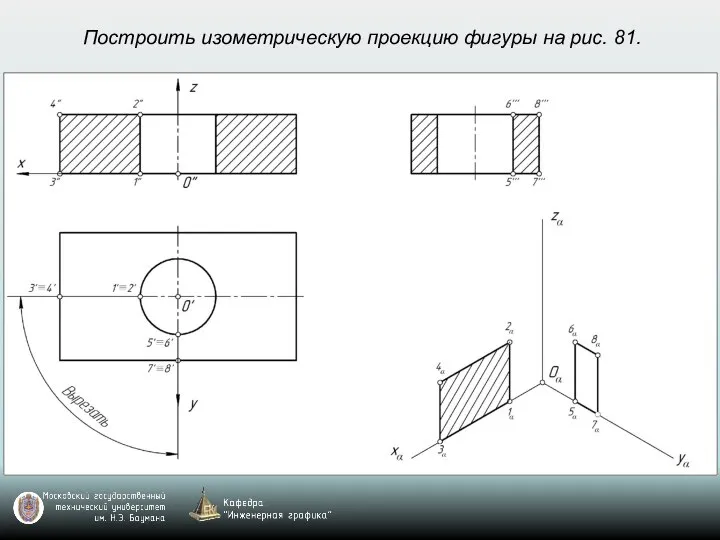
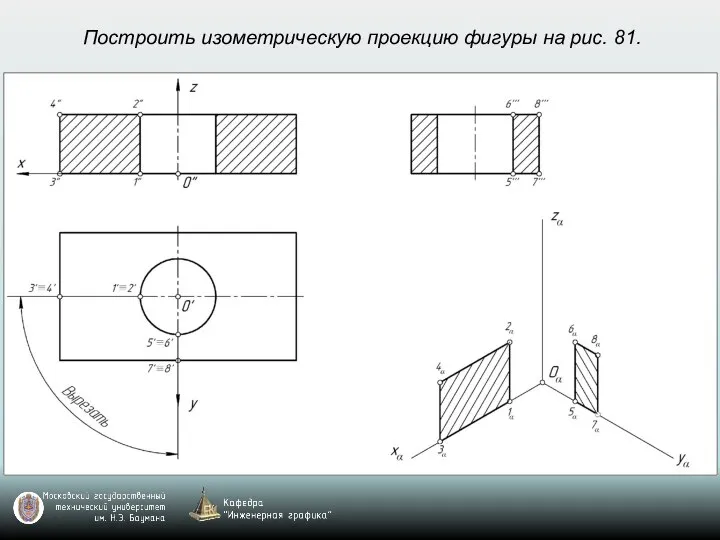
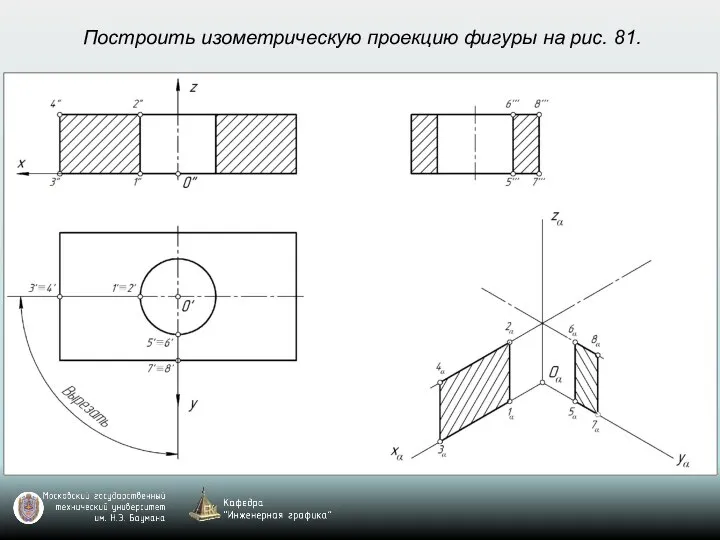
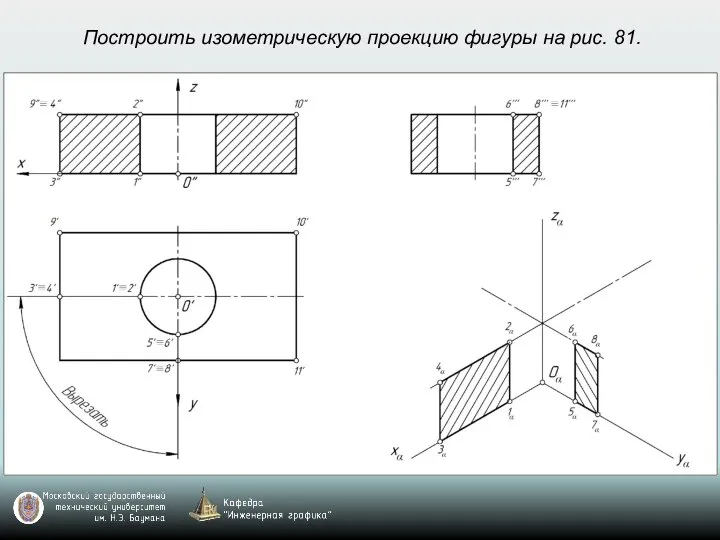
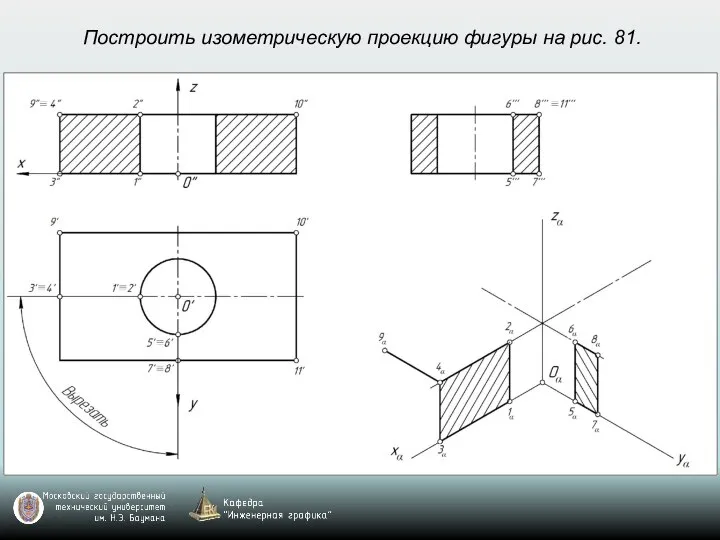
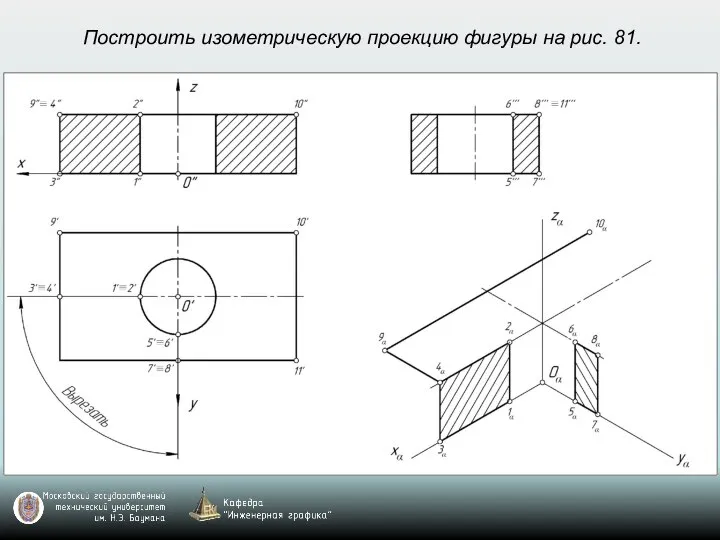
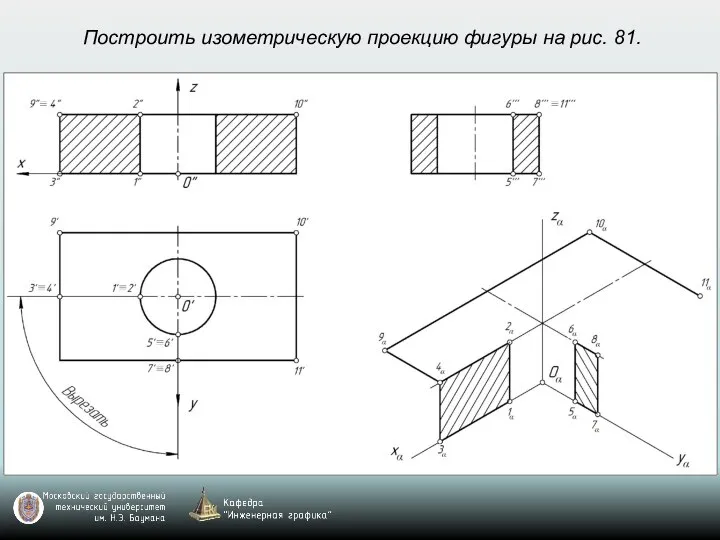
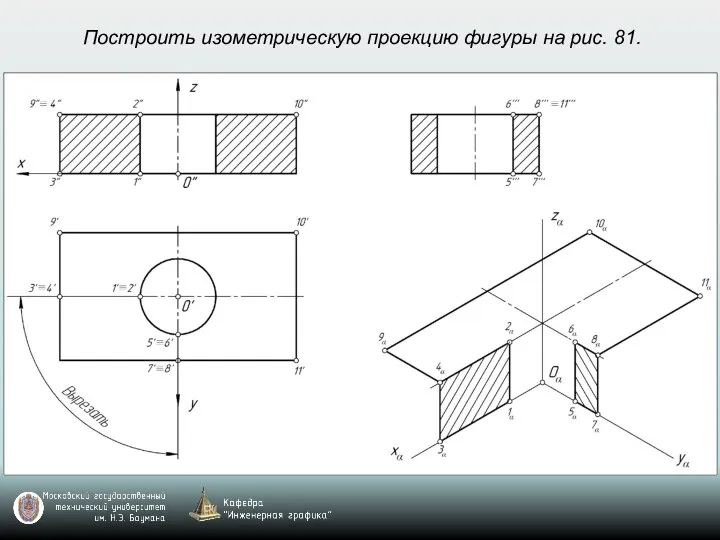
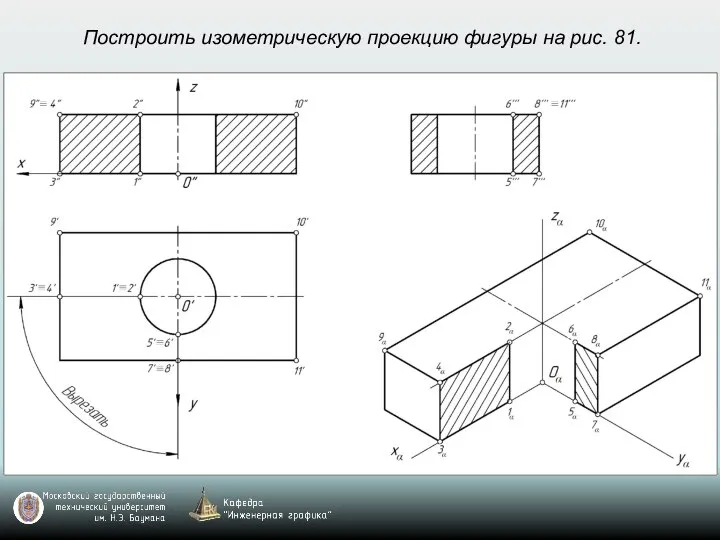
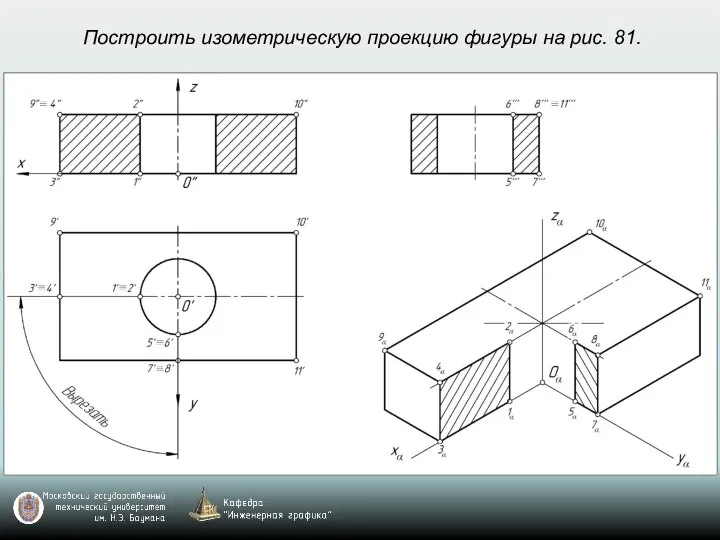
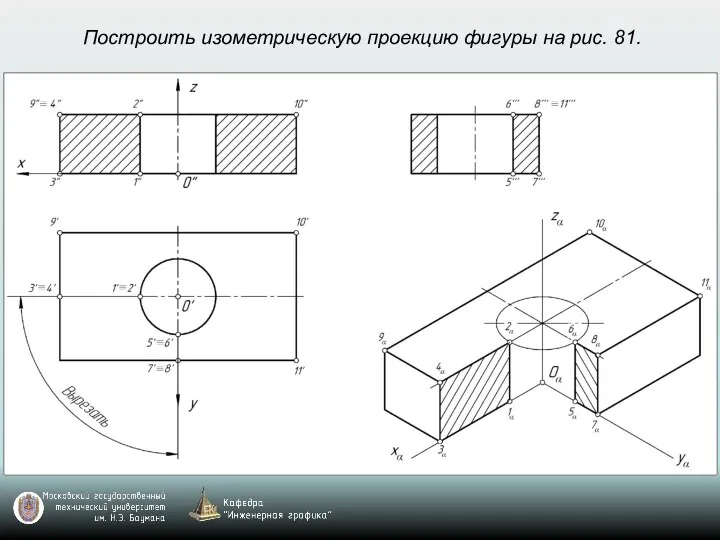
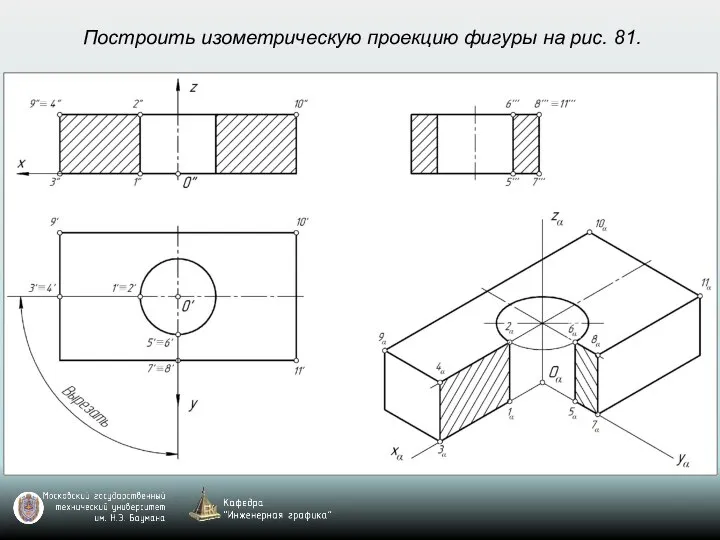
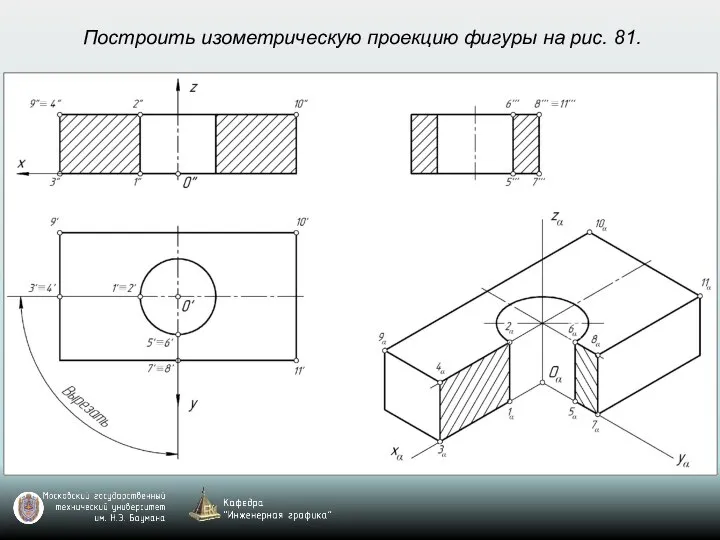
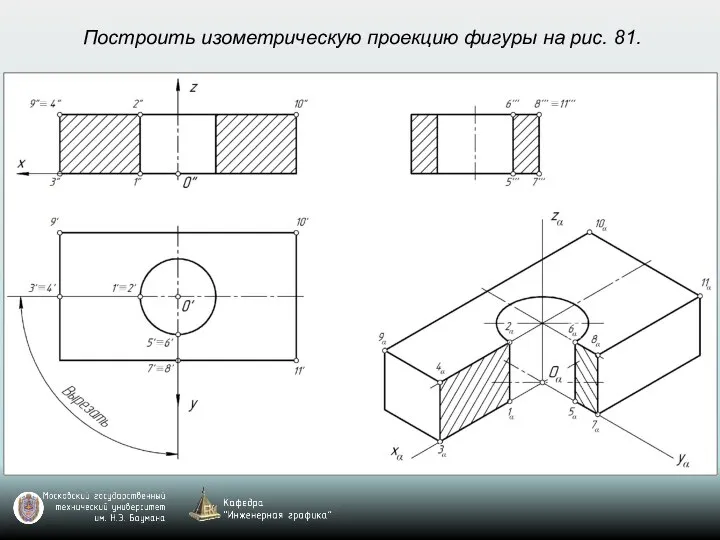
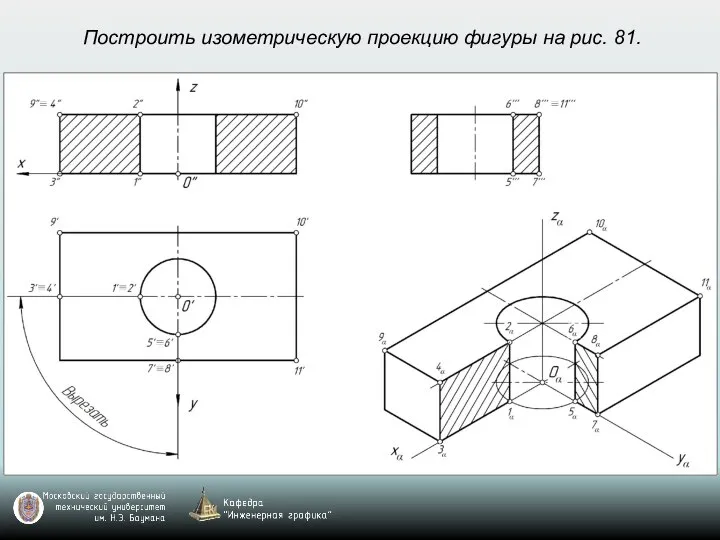
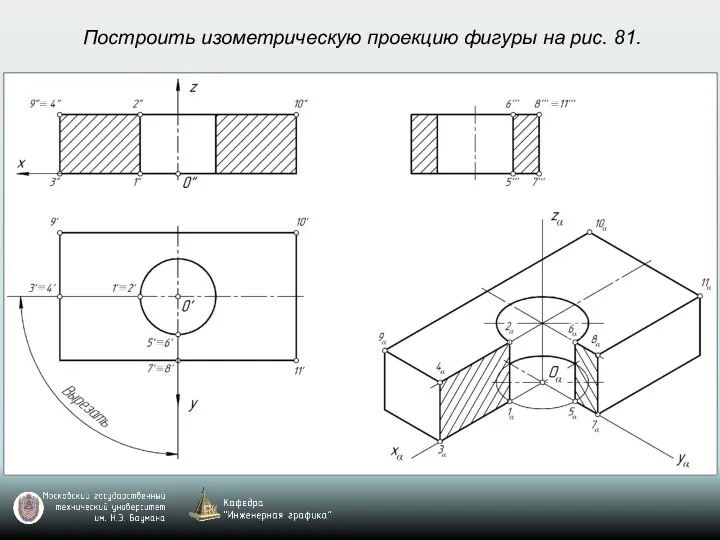
- 69. Построить изометрическую проекцию фигуры на рис. 81.
- 70. Построить изометрическую проекцию фигуры на рис. 81.
- 71. Построить изометрическую проекцию фигуры на рис. 81.
- 72. Построить изометрическую проекцию фигуры на рис. 81.
- 73. Построить изометрическую проекцию фигуры на рис. 81.
- 74. Построить изометрическую проекцию фигуры на рис. 81.
- 75. Построить изометрическую проекцию фигуры на рис. 81.
- 76. Построить изометрическую проекцию фигуры на рис. 81.
- 77. Построить изометрическую проекцию фигуры на рис. 81.
- 78. Построить изометрическую проекцию фигуры на рис. 81.
- 79. Построить изометрическую проекцию фигуры на рис. 81.
- 80. Построить изометрическую проекцию фигуры на рис. 81.
- 81. Построить изометрическую проекцию фигуры на рис. 81.
- 82. Построить изометрическую проекцию фигуры на рис. 81.
- 83. Построить изометрическую проекцию фигуры на рис. 81.
- 84. Построить изометрическую проекцию фигуры на рис. 81.
- 85. Построить изометрическую проекцию фигуры на рис. 81.
- 86. Построить изометрическую проекцию фигуры на рис. 81.
- 87. Построить изометрическую проекцию фигуры на рис. 81.
- 88. Построить изометрическую проекцию фигуры на рис. 81.
- 89. Построить изометрическую проекцию фигуры на рис. 81.
- 90. Построить изометрическую проекцию фигуры на рис. 81.
- 91. Построить изометрическую проекцию фигуры на рис. 81.
- 92. Построить изометрическую проекцию фигуры на рис. 81.
- 93. Построить изометрическую проекцию фигуры на рис. 81.
- 94. Построить изометрическую проекцию фигуры на рис. 81.
- 95. Построить изометрическую проекцию фигуры на рис. 81.
- 96. Построить изометрическую проекцию фигуры на рис. 81.
- 97. Построить изометрическую проекцию фигуры на рис. 81.
- 99. Скачать презентацию


























 ПРОЕКТ «ЗЕЛЕНОЕ ДЕТСТВО»
ПРОЕКТ «ЗЕЛЕНОЕ ДЕТСТВО» тест
тест FLAG OF ENGLAND
FLAG OF ENGLAND  Презентация на тему Час Земли
Презентация на тему Час Земли В 1663 году из гонимых за старую веру образовалась деревня Ново-Алейка. Основатели ее – старообрядцы Матвей и Ларион Лазурины, Валех
В 1663 году из гонимых за старую веру образовалась деревня Ново-Алейка. Основатели ее – старообрядцы Матвей и Ларион Лазурины, Валех Моря, озёра и реки России
Моря, озёра и реки России Проект на тему: Фэн-шуй ( | ) в классной комнате. - презентация
Проект на тему: Фэн-шуй ( | ) в классной комнате. - презентация Презентация на тему Skype
Презентация на тему Skype Булочки синабон
Булочки синабон Человеческий капитал = Профильный актив?!
Человеческий капитал = Профильный актив?! Я и полиция
Я и полиция Исключения из страхового покрытия и основания для освобождения страховщика от осуществления страховой выплаты: правовая природа
Исключения из страхового покрытия и основания для освобождения страховщика от осуществления страховой выплаты: правовая природа  Презентация на тему Античный период
Презентация на тему Античный период  пример РП по ФГОС
пример РП по ФГОС Презентация на тему Плутон
Презентация на тему Плутон ЦРП-2 23.09.22
ЦРП-2 23.09.22 Расширенная программа сессии Кузбасский Университариум Стратега
Расширенная программа сессии Кузбасский Университариум Стратега Сиднейский оперный театр
Сиднейский оперный театр Урок Мир вокруг нас в 1 классе. Автор: учитель начальных классов МОУ СОШ №2 с.Арзгир Концевая Н.Д.
Урок Мир вокруг нас в 1 классе. Автор: учитель начальных классов МОУ СОШ №2 с.Арзгир Концевая Н.Д. Двоичная арифметика
Двоичная арифметика Пышная фатиновая юбка – модный тренд. Кроим и шьем
Пышная фатиновая юбка – модный тренд. Кроим и шьем Обращения
Обращения ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ В ГРУНТАХ
ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ В ГРУНТАХ Роль психолога в период адаптации первоклассников
Роль психолога в период адаптации первоклассников Оборудование для бургерных
Оборудование для бургерных Специальные объекты ландшафтного проектирования. Лекция 3
Специальные объекты ландшафтного проектирования. Лекция 3 Презентация на тему Йемен
Презентация на тему Йемен «Детский мобильный интернет» вовлечение ЦА в создание продукта
«Детский мобильный интернет» вовлечение ЦА в создание продукта