Содержание
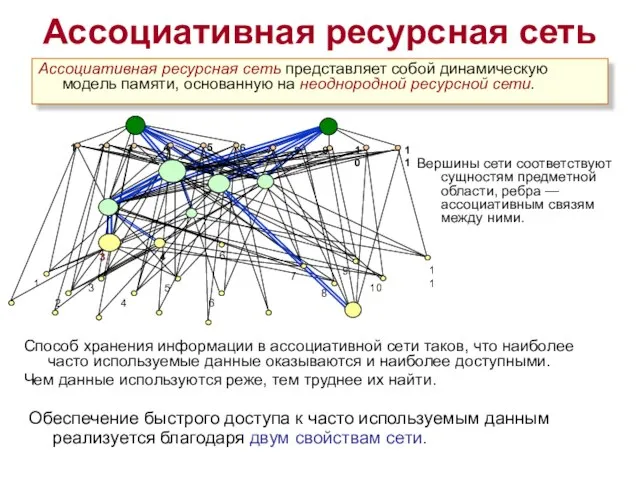
- 2. Ассоциативная ресурсная сеть Ассоциативная ресурсная сеть представляет собой динамическую модель памяти, основанную на неоднородной ресурсной сети.
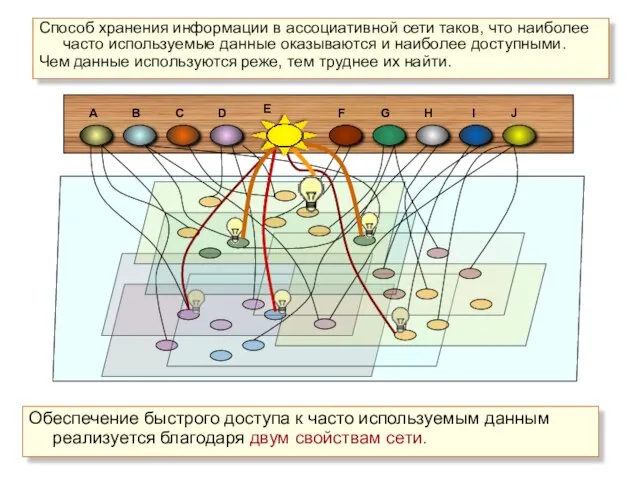
- 3. Способ хранения информации в ассоциативной сети таков, что наиболее часто используемые данные оказываются и наиболее доступными.
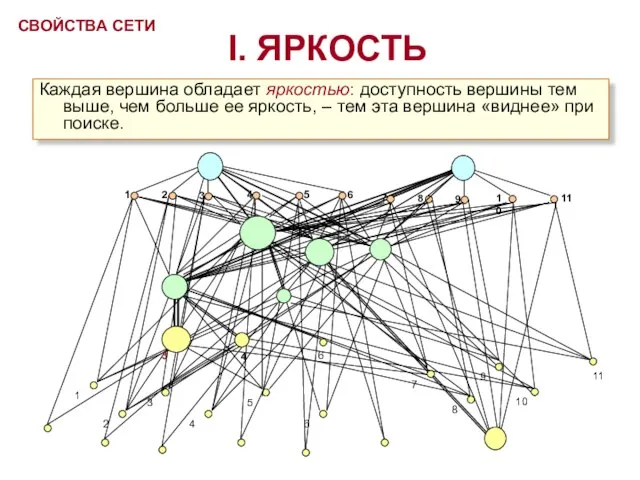
- 4. I. ЯРКОСТЬ Каждая вершина обладает яркостью: доступность вершины тем выше, чем больше ее яркость, – тем
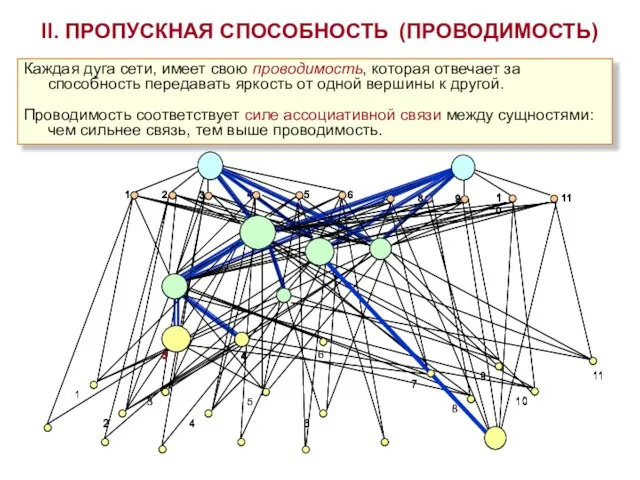
- 5. 11 Каждая дуга сети, имеет свою проводимость, которая отвечает за способность передавать яркость от одной вершины
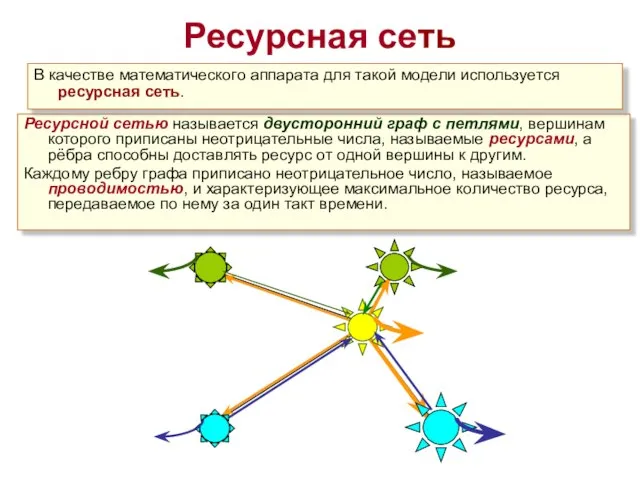
- 6. Ресурсная сеть Ресурсной сетью называется двусторонний граф с петлями, вершинам которого приписаны неотрицательные числа, называемые ресурсами,
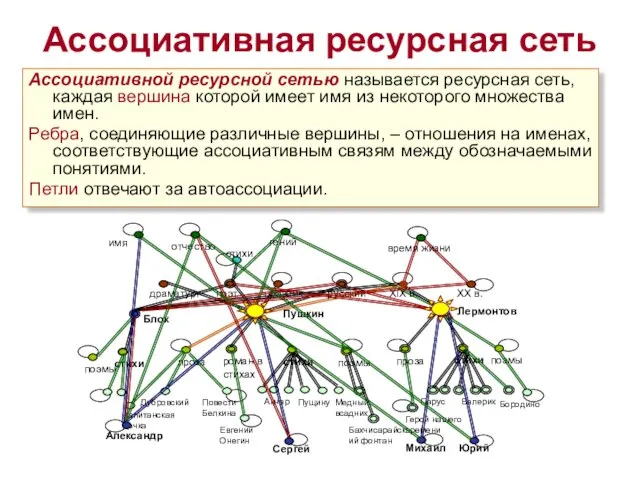
- 7. Ассоциативная ресурсная сеть Ассоциативной ресурсной сетью называется ресурсная сеть, каждая вершина которой имеет имя из некоторого
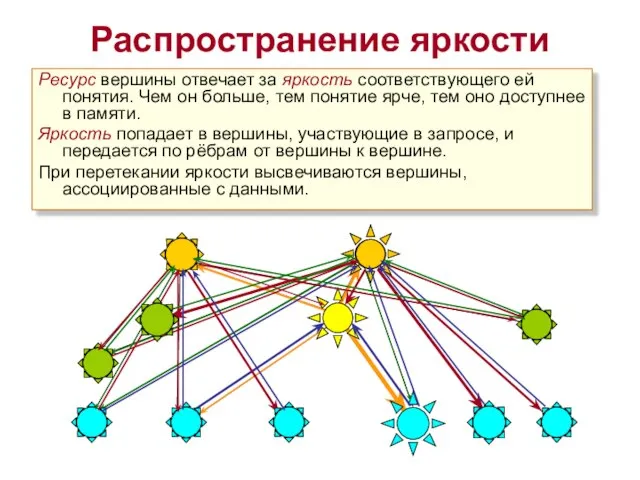
- 8. Ресурс вершины отвечает за яркость соответствующего ей понятия. Чем он больше, тем понятие ярче, тем оно
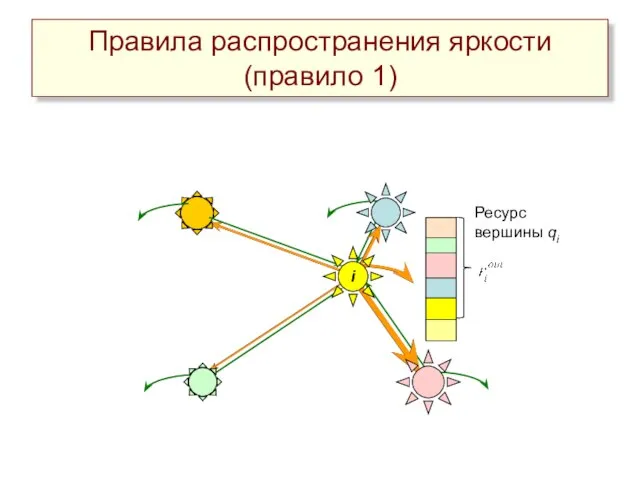
- 9. Ресурс вершины qi Правила распространения яркости (правило 1) i
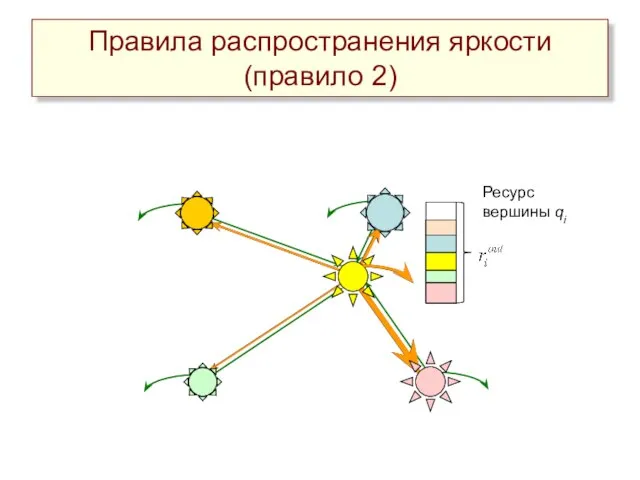
- 10. Ресурс вершины qi Правила распространения яркости (правило 2)
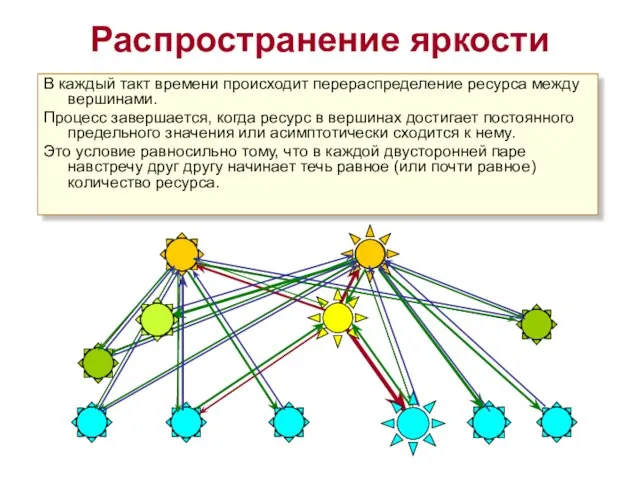
- 11. В каждый такт времени происходит перераспределение ресурса между вершинами. Процесс завершается, когда ресурс в вершинах достигает
- 12. Изменение топологии сети Особенностью предложенной модели является динамическое изменение ее топологии всякий раз после того, как
- 13. Пока в сеть не поступает запросов, она находится в неактивном состоянии. В сети вводится время двух
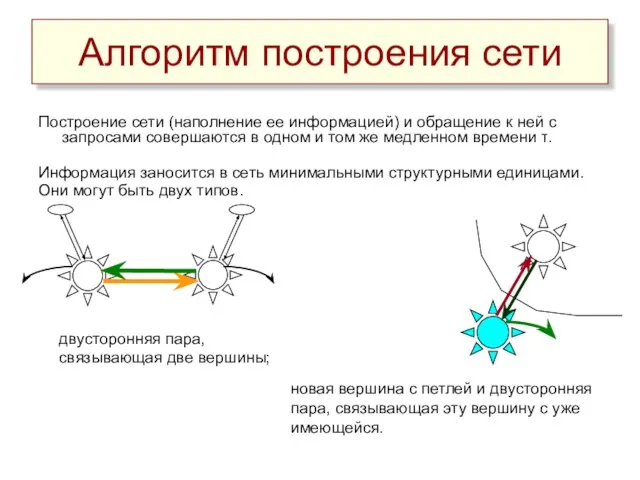
- 14. Алгоритм построения сети Построение сети (наполнение ее информацией) и обращение к ней с запросами совершаются в
- 15. Проводимость петли увеличивается на заданный «квант проводимости» всякий раз, когда вершина связывается с новой вершиной, или
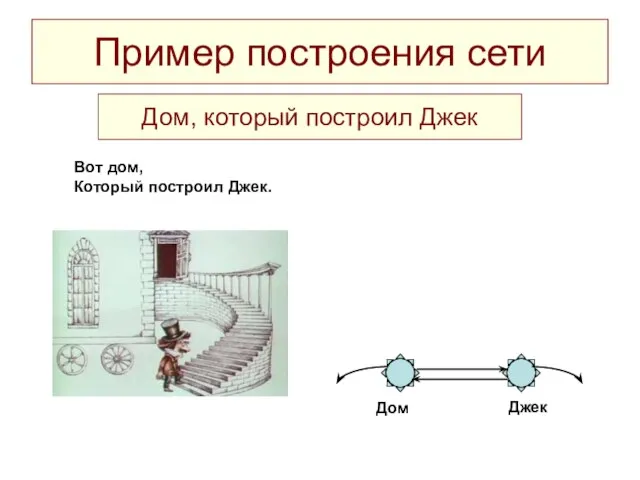
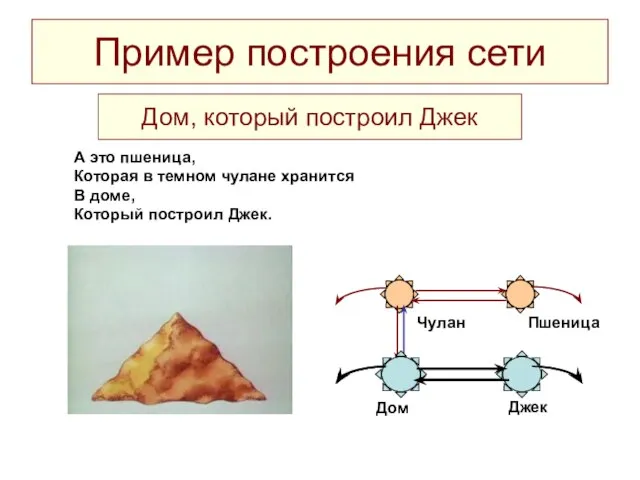
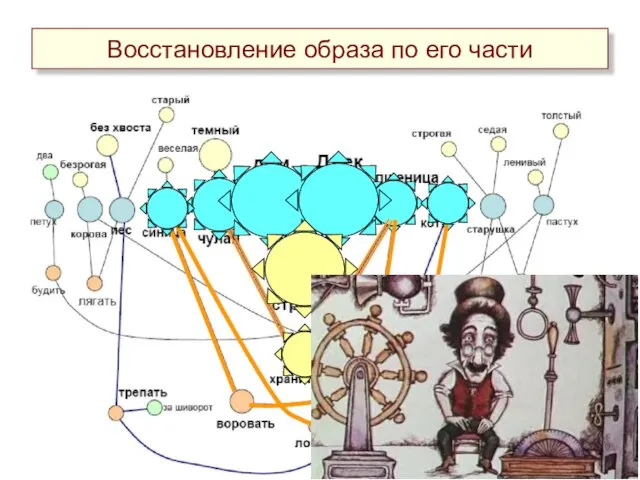
- 16. Пример построения сети Вот дом, Который построил Джек. Дом Джек Дом, который построил Джек
- 17. А это пшеница, Которая в темном чулане хранится В доме, Который построил Джек. Пример построения сети
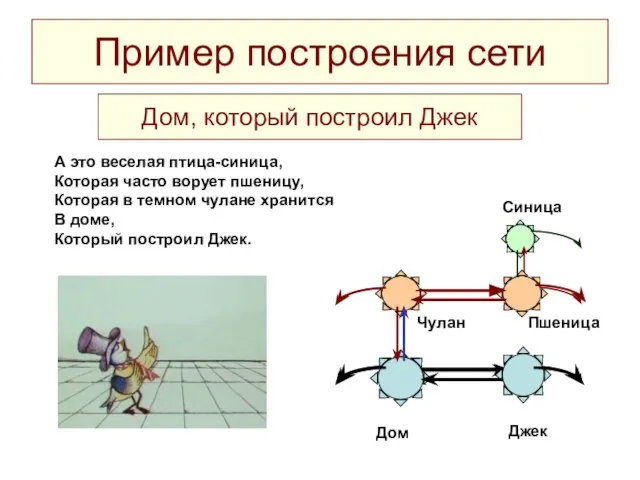
- 18. Пример построения сети Дом Джек Дом, который построил Джек Пшеница Чулан А это веселая птица-синица, Которая
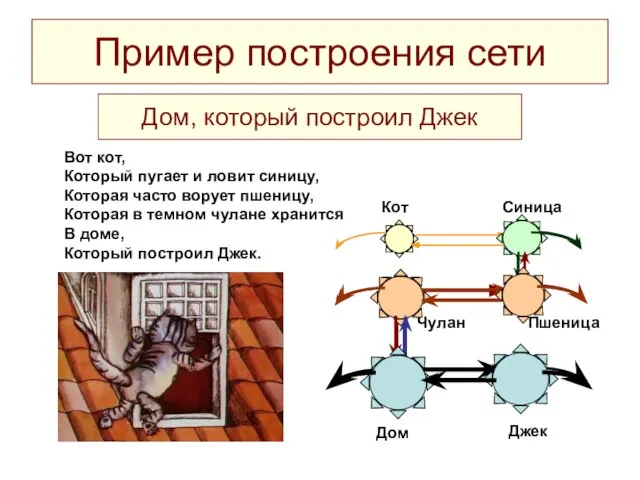
- 19. Пример построения сети Дом Джек Дом, который построил Джек Пшеница Чулан Синица Вот кот, Который пугает
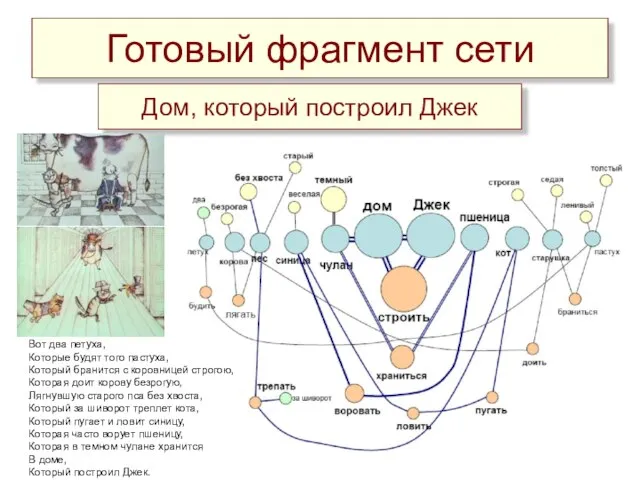
- 20. Вот два петуха, Которые будят того пастуха, Который бранится с коровницей строгою, Которая доит корову безрогую,
- 21. Восстановление образа по его части
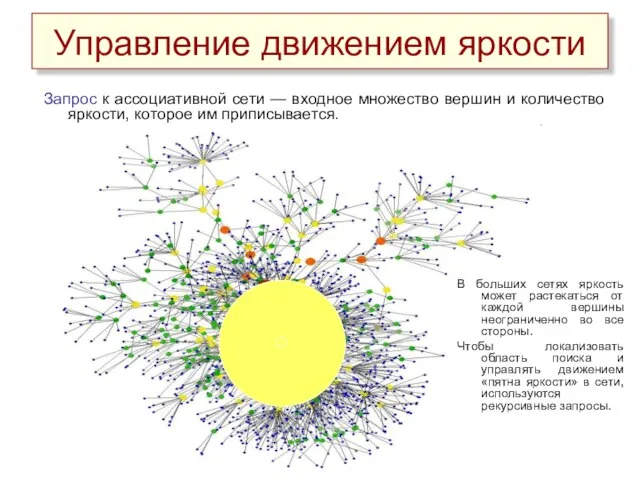
- 22. Управление движением яркости Запрос к ассоциативной сети — входное множество вершин и количество яркости, которое им
- 23. Под рекурсивным запросом будем понимать многократный запрос, входное множество вершин которого изменяется в зависимости от выходного
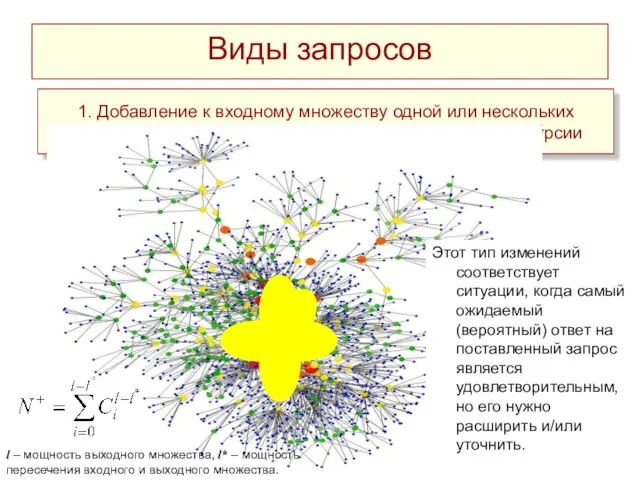
- 24. Виды запросов 1. Добавление к входному множеству одной или нескольких вершин из выходного множества предыдущего шага
- 25. 2. Удаление одной или нескольких вершин из входного множества предыдущего запроса 2. a) Удаляются вершины из
- 26. 2. Удаление одной или нескольких вершин из входного множества предыдущего запроса 2. b) Удаляются вершины из
- 27. Комбинируя все возможные сочетания добавления и удаления вершин, получим . различных множеств, каждое из которых претендует
- 28. Операции над графами 1. Оператор T(G) – транзитивное замыкание графа G. Действует он следующим образом: для
- 29. Операции над графами 3. Оператор Е (удаление вершин) применяется к одному графу. Запись: (G) означает, что
- 30. Операции над графами Будем считать, что сначала к графу GIn(i) применяется оператор Е, а затем к
- 31. Заключение Топология изменяется автоматически таким образом, что наиболее востребованная информация оказывается наиболее доступной. Ассоциативность сети заключается
- 33. Скачать презентацию











 Архітектура України ХІХ ст
Архітектура України ХІХ ст Обучение правилам чтения
Обучение правилам чтения Презентация на тему Названия месяцев и дней недели
Презентация на тему Названия месяцев и дней недели  Нижний Новгород, 2020
Нижний Новгород, 2020 Weddings in different countries
Weddings in different countries Лев Николаевич Толстой
Лев Николаевич Толстой Название бизнес-плана
Название бизнес-плана 90 лет на планете Земля
90 лет на планете Земля Gli ospiti di Jerry. Chi è?
Gli ospiti di Jerry. Chi è? Первый день творения (земля, вода, небо)
Первый день творения (земля, вода, небо) Электроснабжение объектов
Электроснабжение объектов Генерация вероятностных автоматов методами Reinforcement Learning
Генерация вероятностных автоматов методами Reinforcement Learning Взаимодействие токов. Магнитное поле
Взаимодействие токов. Магнитное поле Летние Олимпийские игры 2012 в Лондоне
Летние Олимпийские игры 2012 в Лондоне Финансовый калькулятор
Финансовый калькулятор Абсцесс и гангрена легких
Абсцесс и гангрена легких Marshrutnaya set s perechnem ostanovochnyh punktov
Marshrutnaya set s perechnem ostanovochnyh punktov Nikolay Mikhaylovich Przhevalsky and Russian geography and exploration.
Nikolay Mikhaylovich Przhevalsky and Russian geography and exploration. Дисграфия как одна из причин школьной неуспешности по русскому языку
Дисграфия как одна из причин школьной неуспешности по русскому языку Отчет по производственной практике
Отчет по производственной практике Публичный отчет директора МВ(с)ОУ О(с)ОШ №1
Публичный отчет директора МВ(с)ОУ О(с)ОШ №1 СПБ 2018-2019. Наше маленькое путешествие
СПБ 2018-2019. Наше маленькое путешествие Иван Грозный
Иван Грозный Артериальная гипертония.Антигипертензивные препараты.
Артериальная гипертония.Антигипертензивные препараты. Буквы потерялись
Буквы потерялись МЕТОДЫ ДИАГНОСТИКИ ИНФЕКЦИОННЫХ ЗАБОЛЕВАНИЙ
МЕТОДЫ ДИАГНОСТИКИ ИНФЕКЦИОННЫХ ЗАБОЛЕВАНИЙ Дом и вещи
Дом и вещи Презентация на тему Великая отечественная война на Кубани
Презентация на тему Великая отечественная война на Кубани