Реляционная модель. Реляционная алгебра и реляционное исчисление

Рассматриваемые вопросы:
1.Реляционная модель
- Краткий обзор истории реляционной модели
- Используемая терминология - Альтернативная терминология
- Математические отношения
- Отношения и их свойства в базе данных
- Реляционные ключи
- Представление схем в реляционной базе данных
- Реляционная целостность
2.Реляционные языки
3.Реляционная алгебра
- Унарные операции реляционной алгебры
- Операции с множествами
- Операции соединения
- Деление
4.Реляционное исчисление
- Реляционное исчисление кортежей
- Реляционное исчисление доменов
5.Другие языки

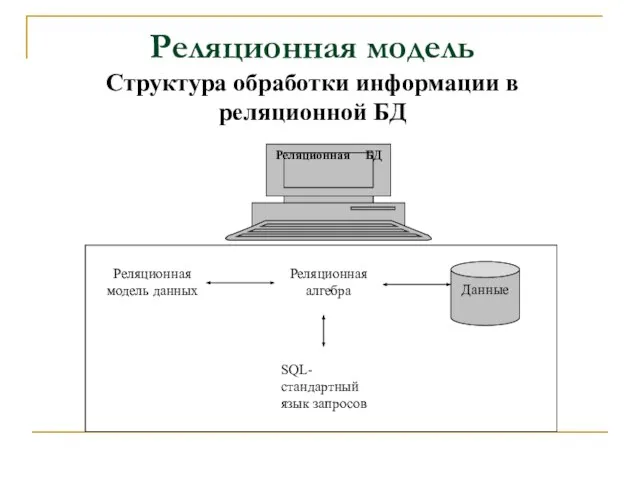
Реляционная модель
Структура обработки информации в реляционной БД

Реляционная модель
Цели создания реляционной модели:
1) Обеспечение высокой степени независимости от данных.
2) Нормализация отношений, т.е. создание отношений без повторяющихся групп.
3) Расширение языков управления данными за счет включения операций над множествами.

Реляционная модель
Используемая терминология
По сколько Кодд, будучи опытным математиком, широко использовал математическую терминологию теории множеств и логики предикатов.
Реляционная модель основана на математическом понятии отношения, физическим представлением которого является таблица.

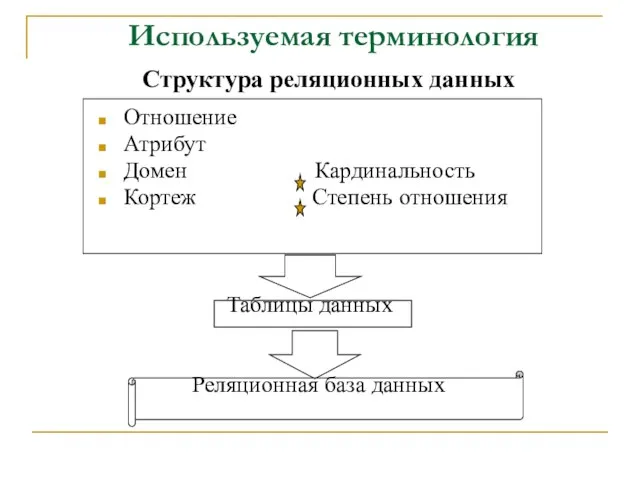
Используемая терминология Структура реляционных данных
Отношение
Атрибут
Домен Кардинальность
Кортеж Степень отношения
Таблицы данных
Реляционная база данных

Используемая терминология
О
Т
Н
О
Ш
Е
Н
И
Е
С Т Е П Е Н Ь
К
А
Р
Д
И
Н
А
Л
Ь
Н
О
С
Т
Ь
АТРИБУТЫ
КОРТЕЖ
Структура реляционных данных

Используемая терминология
Отношение - это плоская таблица(двумерная), состоящая из столбцов и строк.
Атрибут - это поименованный столбец отношения.
Домен - это набор допустимых значений для одного или нескольких атрибутов, благодаря ему пользователь может централизованно определять смысл и источник значений, которые могут получать атрибуты.
Кортеж - это строка отношения.
Кортежи называются расширением, состоянием или телом отношения, которое постоянно меняется.
Описание структуры отношения вместе со спецификацией доменов и любыми другими ограничениями возможных значений атрибутов иногда называют его заголовком (или содержанием (intension)).

Используемая терминология
Степень отношения определяется количеством атрибутов, которое оно содержит.
Кардинальность - это количество кортежей, которое содержит отношение.
Кардинальность - свойство тела отношения (меняется при каждом добавлении или удалении кортежей ).
Реляционная база данных - это набор нормализованных отношений.
Реляционная база данных состоит из отношений, структура которых определяется с помощью особых методов, называемых нормализацией.

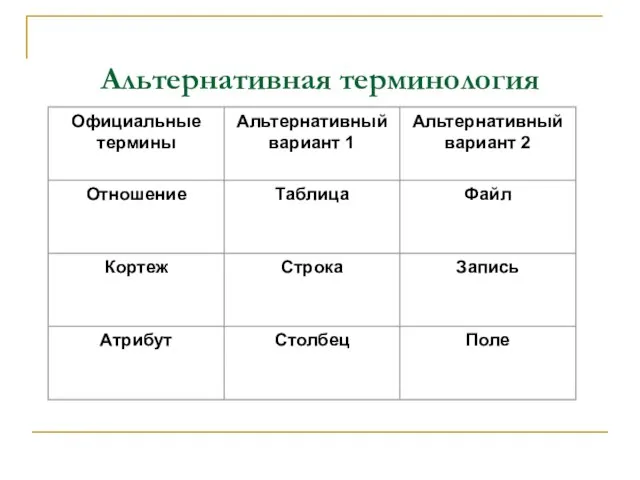
Альтернативная терминология

Отношения и их свойства в базе
данных
Реляционная схема – это имя отношения,
за которым следует множество пар атрибутов и доменов.
атрибуты А1, А2, .... Аn реляционная схема:
домены D1, D2 .... Dn {А1:D1...An:Dn}
В реляционной модели отношение можно представить как произвольное подмножество декартового произведения, а таблица – это физическое представление такого отношения.

Отношения и их свойства в базе
данных
Свойства отношений:
Отношение имеет неповторимое имя.
Каждая ячейка отношения содержит только атомарное (неделимое) значение.
Каждый атрибут имеет уникальное имя.
Значения атрибута берутся из одного и того же домена.
Порядок следования атрибутов не имеет никакого значения.
Каждый кортеж является уникальным, т.е. дубликатов кортежей быть не может.
Порядок следования кортежей в отношении не имеет никакого значения.

Реляционные ключи
Суперкпюч (superkey) – атрибут или множество атрибутов, которое единственным образом идентифицирует кортеж данного отношения.
Потенциальный ключ – это суперключ, который не содержит подмножества, также являющегося суперключом данного отношения.
Потенциальный ключ К для данного отношения R обладает
двумя свойствами:
Уникальность. В каждом кортеже отношения R значение ключа К единственным образом идентифицируют этот кортеж.
Неприводимость. Никакое допустимое подмножество ключа К не обладает свойством уникальности.

Реляционные ключи
Наличие значений-дубликатов в конкретном существующем наборе кортежей доказывает то, что некоторая комбинация атрибутов не может быть потенциальным ключом.
Если ключ состоит из нескольких атрибутов, то он называется составным ключом.
Первичный ключ – это потенциальный ключ, который выбран для уникальной идентификации кортежей внутри отношения.
Поскольку отношение не содержит кортежей-дубликатов, всегда можно уникальным образом идентифицировать каждую его строку.
Это значит, что отношение всегда имеет первичный ключ.

Реляционные ключи
Потенциальные ключи, которые не выбраны
в качестве первичного ключа, называются
альтернативными ключами.
Внешний ключ – это атрибут или множество атрибутов внутри отношения, которое соответствует потенциальному ключу некоторого (может быть, того же самого) отношения.

Представление схем в реляционной базе данных
Реляционная база данных может состоять из произвольного количества отношений.
Концептуальной моделью, или концептуальной схемой, называется множество всех реляционных баз данных.

Реляционная целостность
Модель данных имеет две части:
- управляющую часть, которая определяет типы допустимых операций с данными,
- набор ограничений целостности, которые гарантируют корректность данных.
Определитель NULL вводится в связи с поддержанием правил целостности и указывает, что значение атрибута в настоящий момент неизвестно или неприемлемо для этого кортежа.
Нули и пробелы представляют собой некоторые значения, тогда как ключевое слово NULL призвано обозначать отсутствие какого-либо значения.

Реляционная целостность
Целостность сущностей означает, что в отношении ни один атрибут первичного ключа не может содержать отсутствующих значений, обозначаемых определителем NULL.
Если будет определителя NULL в любой части первичного ключа, это утверждает, что не все его атрибуты необходимы для уникальной идентификации кортежей. Это противоречит определению первичного ключа.

Реляционная целостность
Ссылочная целостность.
Если в отношении существует внешний ключ, то значение внешнего ключа должно либо соответствовать значению потенциального ключа некоторого кортежа в его базовом отношении, либо задаваться определителем NULL.
Корпоративные ограничения целостности данных это дополнительные правила поддержки целостности, определяемые пользователями или администраторами базы данных.

Реляционные языки
Реляционная алгебра - (высокоуровневый) процедурный язык.
Использование: сообщение СУБД о том, как следует построить требуемое отношение на базе одного или нескольких существующих в базе данных отношений.
Реляционное исчисление - непроцедурный язык.
Использование: определения того, каким будет некоторое отношение, созданное на основе одного или нескольких других отношений базы данных.
Реляционно-полный язык
Использование: получение любого отношения, которое можно вывести с помощью реляционного исчисления.

Реляционная алгебра
Реляционная алгебра - теоретический язык операций, который на основе одного или нескольких отношений позволяет создавать другое отношение без изменения самих исходных отношений.

Основные операции реляционной алгебры:
- выборка (selection)
- проекция (рrojection)
- декартово произведение (сartesian product)
- объединение (union)
- разность (set difference)
Дополнительные операции:
- соединения (join)
- пересечения (intersection)
- деления (division)
Реляционная алгебра

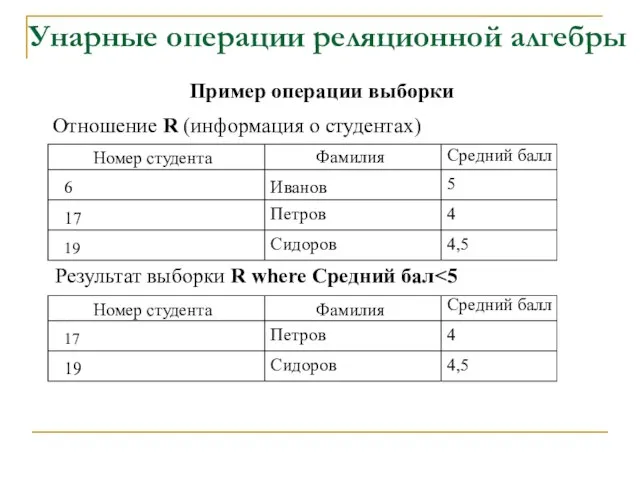
Унарные операции реляционной алгебры
Операция выборки:
Работает с одним отношением R. Определяет результирующее отношение с тем же заголовком, что и отношение R, и телом, состоящим из кортежей, значения атрибутов которых при подстановке в условие (предикат) дают значение истина.

Унарные операции реляционной алгебры
Простейший случай:
X Θ Y - условие (предикат),
Θ – один из операторов сравнения (=, ≠, <, > и т.д.),
X и Y - атрибуты отношения R или скалярные значения.
Синтаксис операции выборки:
R where , или R where (X Θ Y)
Синтаксис на языке SQL:
select * from R where (X θ Y)

Унарные операции реляционной алгебры
Пример операции выборки
Отношение R (информация о студентах)
Результат выборки R where Средний бал<5
Номер студента
Фамилия
Средний балл
6
17
19
Иванов
Петров
Сидоров
5
4
4,5
Номер студента
Фамилия
Средний балл
17
19
Петров
Сидоров
4
4,5

Унарные операции реляционной алгебры
Операция проекции:
Работает с одним отношением R. Определяет новое отношение с заголовком (X,…,Z), содержащее вертикальное подмножество отношения R, создаваемое посредством извлечения значений указанных атрибутов из результата строк-дубликатов.
Синтаксис операции проекции:
R [X,…,Z]
Синтаксис на языке SQL:
Select X, Y,…, Z from R

Унарные операции реляционной алгебры
Пример операции проекции
Отношение R (информация о преподавателях)
Проекция R [Предмет]

Операции с множествами
Декартово произведение R×S
определяет новое отношение, которое является результатом конкатенации
(т.е. сцепления) каждого кортежа из отношения R с каждым кортежем из отношения S.
Синтаксис операции декартового произведения:
R times S
Синтаксис на языке SQL :
Select * from R, S

Операции с множествами
Пример декартового произведения
Отношение R (Студенты)
Отношение S (Предметы)

Отношение R TIMES S
Операции с множествами

Операции с множествами
Операция объединения R S
получается в результате конкатенации R и S,
с образованием одного отношения с тем же заголовком, что и у отношений R и S и телом, состоящим из кортежей, принадлежащих или R, или S, или обоим отношениям (с максимальным количеством кортежей), если кортежи-дубликаты исключены.
Синтаксис операции объединения:
R union S.
Синтаксис на языке SQL:
(Select * from R) union (select * from S)

Операции с множествами
Пример операции объединения
Отношение R (информация о студентах)
Отношение S (информация о студентах)

Объединение отношений R и S
Операции с множествами

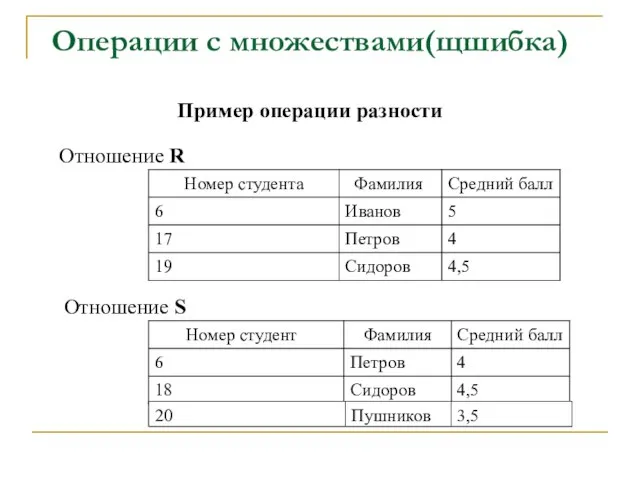
Операции с множествами
Операция разности R-S
определяет отношение с тем же заголовком, что и у отношений R и S, и телом, состоящим из кортежей, принадлежащих отношению R и не принадлежащих отношению S, таких, которые имеются в отношении R, но отсутствуют в отношении S.
Синтаксис операции разности:
R minus S
Синтаксис на языке SQL:
(select * from R) exept (select * from S)

Операции с множествами(щшибка)
Пример операции разности
Отношение R
Отношение S
20
20
Пушников
3,5

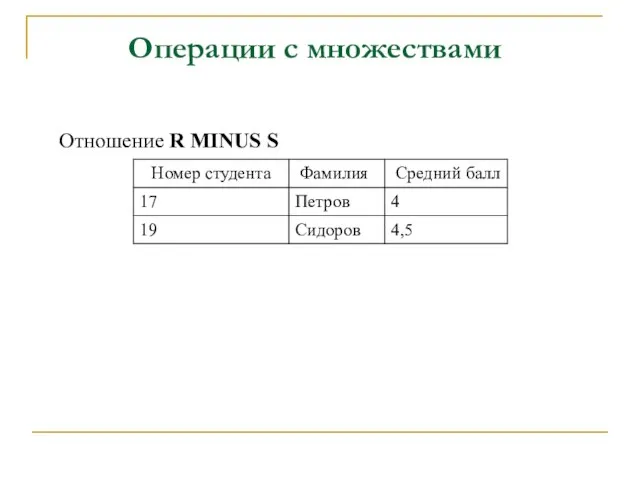
Операции с множествами
Отношение R MINUS S

Операции с множествами
Операция пересечения R∩S
определяет отношение, которое содержит кортежи, присутствующие как в отношении R, так и в отношении S.
Синтаксис операции пересечения:
R intersect S
Синтаксис на языке SQL:
(Select * from R) intersect (select * from S)

Операции с множествами
Пример операции пересечения
Отношение R (информация о студентах)
Отношение S (информация о студентах)

Операции с множествами
Отношение R INTERSECT S

Операции соединения
Операция соединения - комбинация декартового произведения и выборки, эквивалентна операции выборки из декартового произведения двух операндов отношений тех кортежей, которые удовлетворяют условию, указанному в предикате соединения в качестве формулы выборки.
Соединением отношений R и S по условию F называется отношение (R times S) where F
Синтаксис на языке SQL:
Select R.*, S.* from R, S where f

Операции соединения
Типы операций соединения:
- тета-соединение
- соединение по эквивалентности (частный случай тета-соединения)
- естественное соединение
- внешнее соединение
- полусоединение

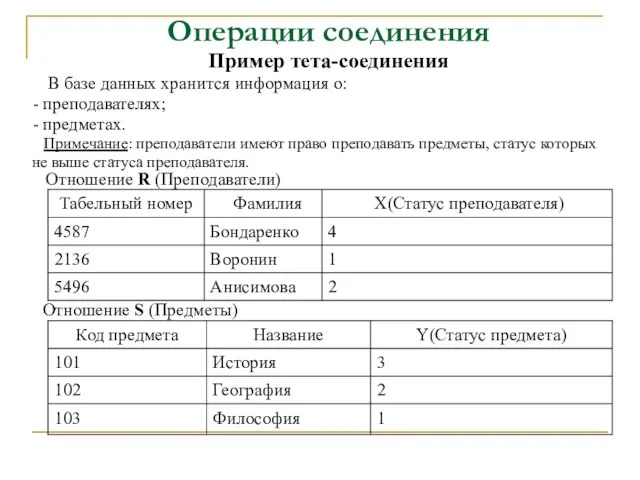
Операции соединения
Тета-соединение определяет отношение,
которое содержит кортежи из декартового произведения отношений R и S, удовлетворяющие предикату F.
Предикат F имеет вид , где - один из
операторов сравнения (<, <=, >, >=, = или -=).
Θ-соединением отношения R по атрибуту X с отношением S
по атрибуту Y называют отношение (R times S) where (X Θ Y).
Синтаксис на языке SQL:
Select * from R, S where (R.X θ S.Y)

Операции соединения
Пример тета-соединения
В базе данных хранится информация о:
- преподавателях; - предметах.
Примечание: преподаватели имеют право преподавать предметы, статус которых
не выше статуса преподавателя.
Отношение R (Преподаватели)
Отношение S (Предметы)

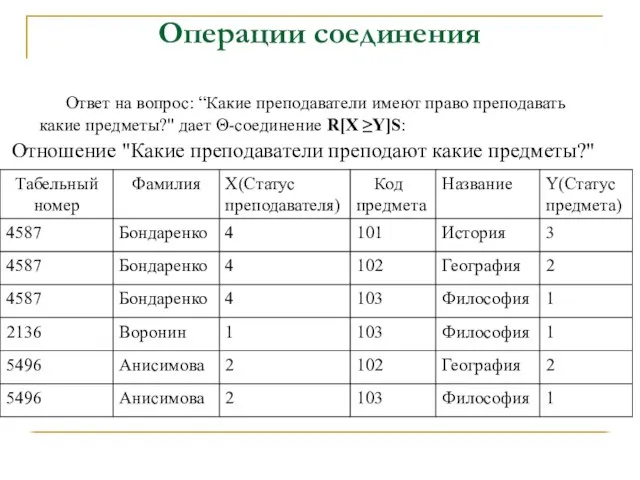
Операции соединения
Ответ на вопрос: “Какие преподаватели имеют право преподавать какие предметы?" дает Θ-соединение R[X ≥Y]S:
Отношение "Какие преподаватели преподают какие предметы?"

Операции соединения
Экви-соединение (соединение по эквивалентности) - частный случай
Θ-соединения, когда Θ есть просто равенство
(предикат F содержит только оператор равенства (=)).
Синтаксис экви-соединения:
R[X=Y]S
Синтаксис на языке SQL:
select R.*, S .* from R, S where (R.X = S.Y)

Операции соединения(Ошибка)
Пример экви-соединения
Отношение S (Студенты)
Отношение P (Предметы)

Операции соединения
Отношение SP (Изучение)
Ответ на вопрос: "Какие предметы изучаются студентами? “, дает экви-соединение S[SNUM= SNUM]SP. Т.к. в отношениях имеются одинаковые атрибуты, то требуется сначала их переименовать.
Получаем: (S rename SNUM as SNUM 1)[SNUM1= SNUM2](SP rename SNUM as SNUM2).

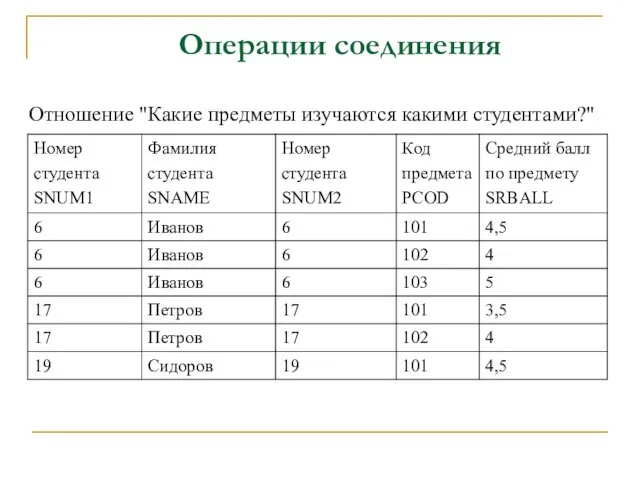
Операции соединения
Отношение "Какие предметы изучаются какими студентами?"

Операции соединения
Естественное соединене - соединение по эквивалентности двух отношений R и S, выполненное по всем общим атрибутам, из результатов которого исключается по одному экземпляру каждого общего атрибута.
Синтаксис естественного соединения:
R join S.
Естественное соединение производится по всем одинаковым атрибутам.

Операции соединения
Пример естественного соединения
Упрощенная запись:
Ответ на вопрос "Какие предметы изучаются какими студентами?“ в виде естественного соединения трех отношений S join SP join P:
Отношение S JOIN SP JOIN P

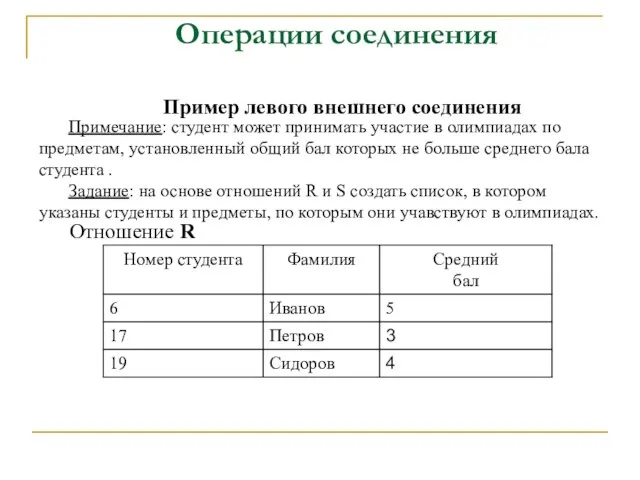
Операции соединения
Операция внешнего соединения используется при соединении двух отношений, столбцы которых имеют несовпадающие значения.
Внешнее соединение : левое и правое.
Левое внешнее соединение :
кортежи отношения R, не имеющие совпадающих значений в общих столбцах отношения S, также включаются в результирующее отношение.
Обозначения отсутствующих значений во втором
отношении - определитель NULL.

Примечание: студент может принимать участие в олимпиадах по предметам, установленный общий бал которых не больше среднего бала студента .
Задание: на основе отношений R и S создать список, в котором указаны студенты и предметы, по которым они учавствуют в олимпиадах.
Операции соединения
Пример левого внешнего соединения
Отношение R

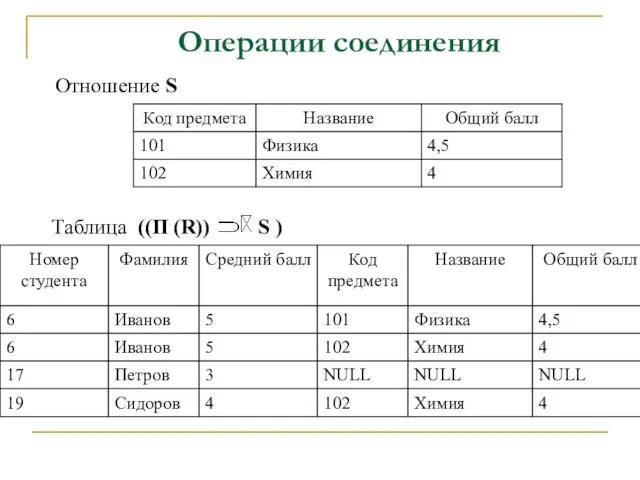
Отношение S
Таблица ((П (R)) S )
Операции соединения

Операции соединения
Правое внешнее соединение:
в результирующем отношении содержатся все кортежи правого отношения.
Полное внешнее соединение:
в результирующее отношение помещаются все кортежи из обоих отношений и для обозначения несовпадающих значений кортежей используются определители NULL.

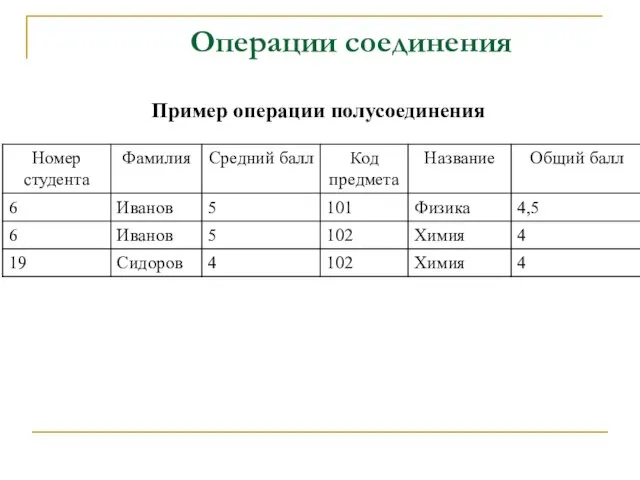
Операции соединения
Операция полусоединения :
определяет отношение, которое содержит те кортежи отношения R, которые входят в соединение отношений R и S.
Формулировка операции полусоединения с помощью операторов проекции и соединения:
где А - набор всех атрибутов в отношении R.

Пример операции полусоединения
Операции соединения

Операция деления
Пусть:
- отношение R определено на множестве атрибутов А;
- отношение S — на множестве атрибутов В;
- В А;
- С=А-В (С является множеством атрибутов отношения R, которые не являются атрибутами отношения S).
Результат деления R S - набор кортежей отношения R, определенных на множестве атрибутов С, которые соответствуют комбинации всех кортежей отношения S.

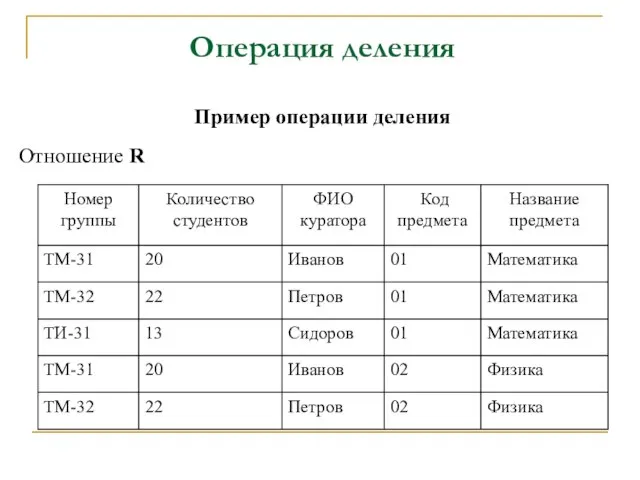
Операция деления
Пример операции деления
Отношение R

Отношение S
T1:Select’Код предмета’, ’Название предмета’ from R
Операция деления

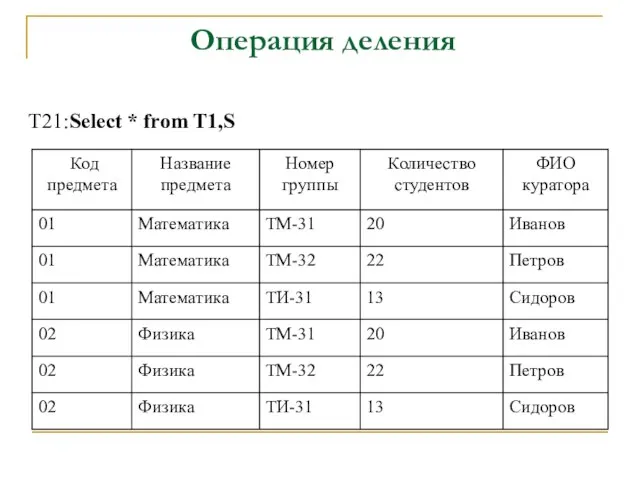
T21:Select * from T1,S
Операция деления

T22: (Select * from T21) exept (Select * from R)
T2: Select ’Код предмета’, ’Название предмета’ from T22
Операция деления
Р=T1-T2
Код предмета
Название предмета
01
Математика

Реляционное исчисление
Происхождение названия “реляционное исчисление”:
от части символьной логики, которая называется исчислением предикатов.
Реляционное исчисление существует в двух формах:
- реляционного исчисления кортежей;
- реляционного исчисления доменов.

Реляционное исчисление
Предикат в логике первого порядка ─ истинностная функция с параметрами.
Суждение ─ выражение, которое принимает функция после подстановки значений вместо параметров.
Суждение: истинное и ложное.
Пусть: Р - предикат;
х - переменная.
Тогда: - множество всех значений х, при которых суждение Р – истина.
Предикаты могут соединяться с помощью логических операторов: (AND), (ОR) и (NOT) с образованием составных предикатов.

Реляционное исчисление кортежей
Задача реляционного исчисления кортежей: нахождение кортежей, для которых предикат является истинным.
Исчисление основано на переменных кортежа.
Переменными кортежа - переменные, областью определения которых является указанное отношение.

Пример
Запрос:
“Выбрать атрибуты № склада, адрес,идент. код, дата,ФИО заказчика для заказов с количеством >60"
Запись запроса:
{ S | R( S ) ^ S.количество> 60}
Пояснение:
Выражение “S.количество часов” - значение атрибута количество часов для кортежа.
Реляционное исчисление кортежей

Реляционное исчисление кортежей
Два типа кванторов, используемых для указания количества экземпляров, к которым должен быть применен предикат:
- квантор существования (символ “существует”): используется в формуле, которая должна быть истинной хотя бы для одного экземпляра;
- квантор общности (символ “для всех”): используется в выражениях, которые относятся ко всем экземплярам.

Пример применения квантора существования
Студент (S) ^ {Зв} (Год рождения(B) ^ (В.имя=S.имя) ^ В. группа='ТИ-31')
Выражение означает: в отношении Год рождения существует кортеж, который имеет такое же значение атрибута имя, что и значение атрибута имя в текущем кортеже S из отношения Студент, а атрибут группа из кортежа В имеет значение ' ТИ-31 '.
Пример применения квантора общности
(B) (В.группа * 'ТИ-31')
Выражение означает: ни в одном кортеже отношения Год рождения значение атрибута группа не равно 'ТМ-31'.
Реляционное исчисление кортежей

Свободные переменные - переменные кортежа, которые неквалифицируются кванторами, в противном случае они называются связанными переменными.
В реляционном исчислении допустимые формулы – только недвусмысленные и небессмысленные последовательности.
Реляционное исчисление кортежей

Правила построения формулы в исчислении предикатов:
1. Если Р - n-арная формула (предикат с n аргументами),
t1, t2,…, tn - константы или переменные,
то Р (t1, t2,…, tn) - правильно построенная формула.
2. Если t и t2 - константы или переменные из одного домена,
- один из операторов сравнения (<, <=, >, >=, -=),
то t1 t2 - правильно построенная формула.
3. Если F1, F2 - формулы,
то F1 F2 - конъюнкция формул,
F1 F2 - дизъюнкция,
- отрицание.
4. Если F1 - формула со свободной переменной X,
то F(Х) и F(Х) - также формулы.
Реляционное исчисление кортежей

Реляционное исчисление доменов
Значения переменных, используемых в реляционном исчислении доменов берутся из доменов, а не из кортежей отношений.
Путь: Р(d1, d2,…, dn) - предикат;
d1, d2,…, dn - переменные.
Тогда:{ d1, d2,…, dn |Р(d1, d2,…, dn)}- множество всех переменных домена, для которых предикат - истина.
Выражение R(х,у) - истинное тогда и только тогда, когда в отношении R имеется кортеж со значениями х и у в двух его атрибутах.

Пример
Найти: имена всех менеджеров, зарплата которых превышает 2500 гривен.
{Имя, Фамилия ‌‌ должность, зарплата
( (фамилия,должность,зарплата) должность= ‘менеджер’ зарплата>2500)}
Реляционное исчисление доменов

Другие языки
Дополнительные категории реляционных языков:
- на основе преобразований;
- графические языки;
- языки четвертого поколения.
Языки на основе преобразований -
класс непроцедурных языков
Используют отношения для преобразования исходных
данных к требуемому виду
(примеры: SQUARE , SEQUEL и его версии, SQL).