Решение иррациональных уравнений

Содержание
Эпиграф.
Виды уравнений.
Определение иррациональных уравнений.
Упражнения на распознавание видов уравнений.
Работаем устно.
Методы решения.
Графический метод.
Функционально-графический метод.
Решите уравнения.
Возведение в степень (алгоритм 1).
Алгоритм 2.
Пример по алгоритму 1.
Пример по алгоритму 2.
Специальные методы решения уравнений.
Справка по ОДЗ.
Справка. Корень n-й степени.
Справка. Модуль.
Об авторе.

Именно математика
дает надежнейшие правила:
кто им следует – тому
не опасен обман чувств.
Л. Эйлер

Виды уравнений
Целые уравнения
Дробно-рациональные
Иррациональные
Тригонометрические
Показательные
Логарифмические

Определение
Иррациональное уравнение –
уравнение, содержащее
переменную под знаком
корня (радикала).
(примеры)
(справка)

Какие из данных уравнений являются иррациональными?
1.
2.
3.
4.

Работаем устно

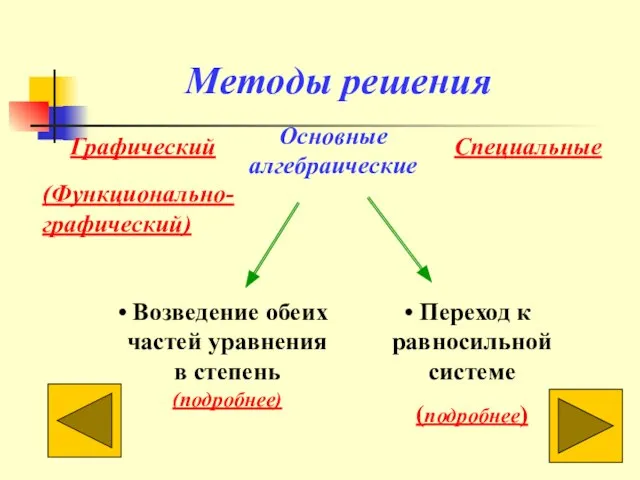
Методы решения
Графический
Основные алгебраические
Переход к равносильной системе
(подробнее)
Специальные
Возведение обеих частей уравнения в степень
(подробнее)
(Функционально-
графический)

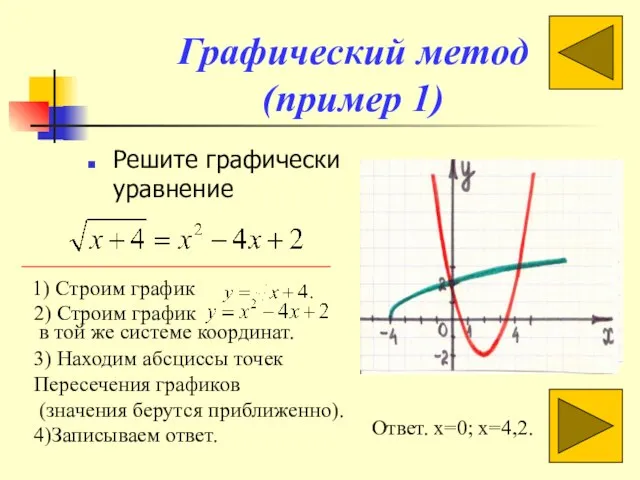
Графический метод
(пример 1)
Решите графически уравнение
Ответ. x=0; x=4,2.
1) Строим график
2) Строим график
в той же системе координат.
3) Находим абсциссы точек
Пересечения графиков
(значения берутся приближенно).
4)Записываем ответ.

Функционально-графический
метод
Пример: решите уравнение
f(x)=
g(x)=5-x, убывает на D(g).
Уравнение f(x)=g(x) имеет не более одного
корня.
4. Подбором находим, что X=2.
Ответ. 2.
- возрастает на D(f).
Решение.

Решите уравнения
(алгоритм 2)
(алгоритм 1)
((алгоритм)

Алгоритм 1
При n – четном
Уедини корень (если необходимо);
Возведи обе части уравнения в степень n;
Если необходимо, то выполни п.1;
Реши полученное уравнение;
Выполни проверку!
Запиши ответ.
(к методам)

Алгоритм 2
При n - нечетном
Уедини корень (если необходимо);
Возведи обе части уравнения в степень n;
Если необходимо, то выполни п.1;
Реши полученное уравнение;
Запиши ответ.
(к методам)

Возведение в степень
Решение.
Возведем обе части уравнения в квадрат:
Преобразуем:
Проверка.
Если x=1, то в левой части 0, в правой части 0,
0=0 (верно).
Если x=-2, то в левой части 3, в правой части -3,
3 не равно -3, значит, -2 не является корнем.
Ответ. 1.
*

Возведение в степень
Решение.
Возведем обе части уравнения
в 3-ю степень:
Преобразуем:
Ответ. 0 ; 3.
*

Переход к равносильной
системе
Определить условия (если n –четно), при
которых обе части уравнения неотрицательны;
2. Возвести обе части уравнения в n-ю степень;
3. Составить систему из уравнения и неравенства;
4. Решить систему;
5. Записать ответ.
Определение.

Переход к равносильной
системе
Решение.
Перейдем к равносильной системе
Откуда x=3.
Ответ. 3.
*

Специальные методы решения
Метод пристального взгляда
Найди ОДЗ
Выполни замену
Умножай на сопряженное
Переходи к модулю
Оцени обе части уравнения
(справка)
(справка)
(справка)

Область определения
уравнения (ОДЗ) –
это все значения переменной, при
которых данное уравнение имеет смысл.
Замечание. Если ОДЗ уравнения есть
пустое множество, то говорят, что
данное уравнение не определено на
множестве R и решений заведомо быть
не может.

Справка
Корень n-й степени из а
-
это такое число b, что
Арифметический корень n-й степени:

Справка
Модуль числа:
|a| =
a
-a
0
Расстояние от 0 до точки, изображающей a на
числовой оси

Спасибо за урок!
Успехов в изучении темы!