РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ В МОДЕЛИ ДВИЖЕНИЯ ХИЛЛА

Модель движения Хилла
Уравнения движения:
Коллинеарные точки либрации L1 и L2:
Матрица изохронных производных Ф:

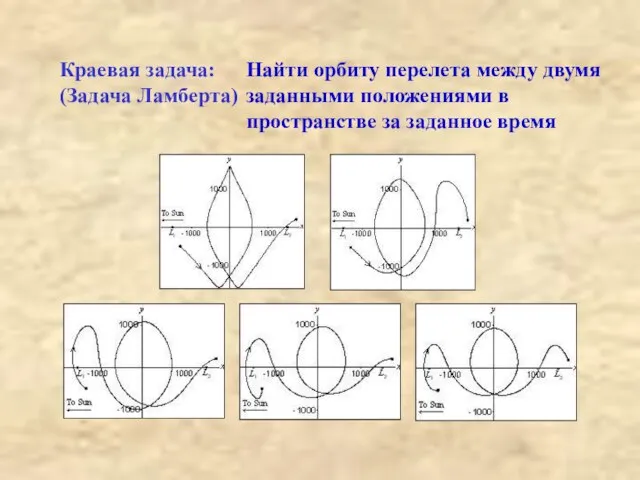
Краевая задача: (Задача Ламберта)
Найти орбиту перелета между двумя заданными положениями в пространстве за заданное время

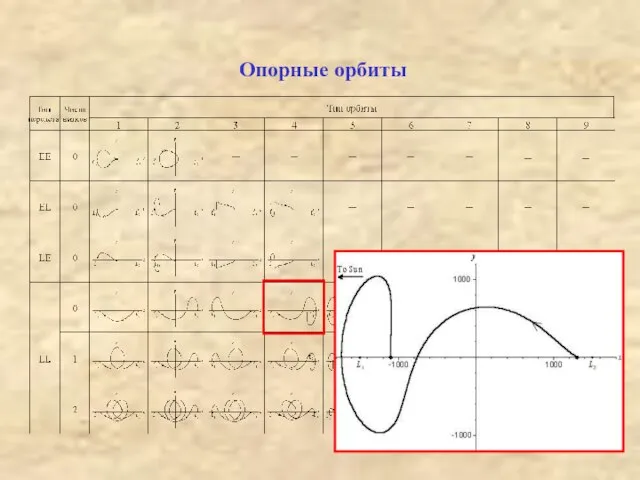
Опорные орбиты

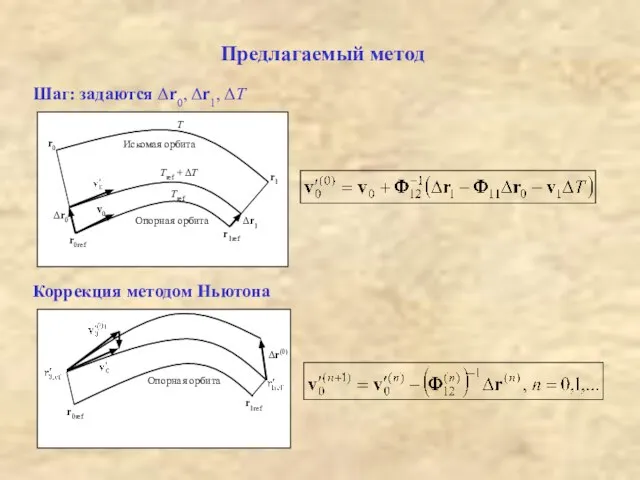
Предлагаемый метод
Шаг: задаются Δr0, Δr1, ΔT
Коррекция методом Ньютона

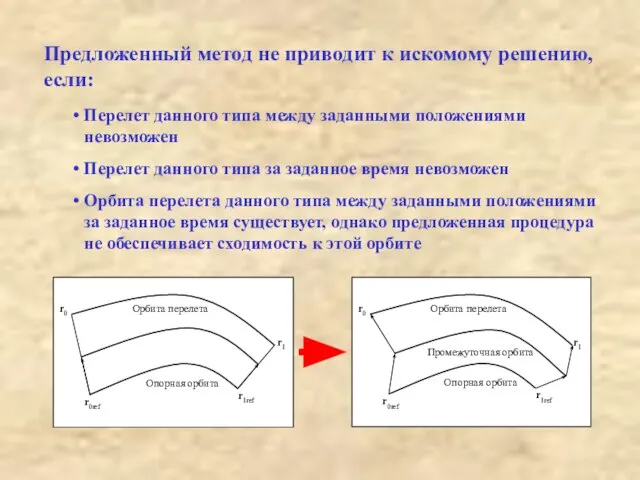
Перелет данного типа между заданными положениями невозможен
Перелет данного типа за заданное время невозможен
Орбита перелета данного типа между заданными положениями за заданное время существует, однако предложенная процедура не обеспечивает сходимость к этой орбите
Предложенный метод не приводит к искомому решению, если:

r0 = {−1400, −800, 300}
r1 = {1800, –500, –200}
T = 300 дней
r0 = {–1400, –800, 0}
r1 = {1800, –500, 0}
T = 260 дней
Промежуточная орбита:
Тип:
Примеры: Перелет между двумя заданными положениями за заданное время

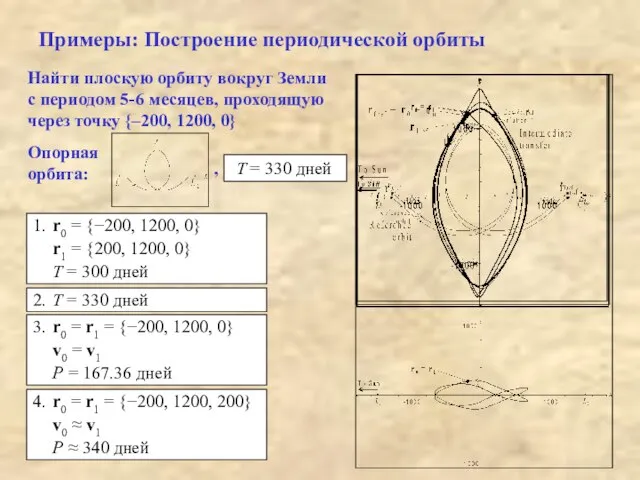
Примеры: Построение периодической орбиты
Найти плоскую орбиту вокруг Земли с периодом 5-6 месяцев, проходящую через точку {–200, 1200, 0}
Опорная орбита:
1. r0 = {−200, 1200, 0}
r1 = {200, 1200, 0}
T = 300 дней
2. T = 330 дней
3. r0 = r1 = {−200, 1200, 0}
v0 = v1
P = 167.36 дней
4. r0 = r1 = {−200, 1200, 200}
v0 ≈ v1
P ≈ 340 дней
, T = 330 дней

Примеры: Построение гало-орбиты
r0 = r1 = {xL1−200, 0, 0} =
= {−1296.56, 0, 0}
v0 = v1
P ≈ 180 дней
Опорная орбита:
P = 178.295 дней
Пространственная гало-орбита:
r0 = {−1296.56, 0, 100}
r1 = {−1296.56, 0, −100}
Tref = 2P, T = 358 дней
180-суточный фрагмент орбиты

Примеры: Перелет Земля – гало-орбита
r0 = {7, 0, 0}
r1 = {–1350, 800, 0}
T = 235 дней
Опорная орбита:
Затем:
r1 = {–1220, 0, 0}
T = 280 дней
И т.д.

Примеры: Перелет между гало-орбитами вокруг L1
Гало-орбиту зададим вектором состояния
x0 = {xL–Δx0, 0, z0, 0, –v0cosϕ0, v0sinϕ0}
Первая гало-орбита:
Вторая гало-орбита:
Опорная орбита:
xL = –1500, Δx0 = –100, z0 = –100
v0 = 155.1 м/с, ϕ0 = 40°
(1)
xL = –1500, Δx0 = –250, z0 = 100
v0 = 254.3 м/с, ϕ0 = 30°
(2)
r0 через 80 дней после x0 (1)
r1 через 170 дней после x0 (2)
T = 70 дней
70-суточный фрагмент орбиты

Примеры: Перелет между гало-орбитами вокруг L1 и L2
Гало-орбиту зададим вектором состояния
x0 = {xL–Δx0, 0, z0, 0, v0cosϕ0, v0sinϕ0}
Первая гало-орбита:
xL = –1500, Δx0 = –100, z0 = –100
v0 = 155.1 м/с, ϕ0 = 140°
Вторая гало-орбита:
xL = 1500, Δx0 = 250, z0 = 100
v0 = 254.3 м/с, ϕ0 = 30°
Орбита перелета:
r0 через 80 дней после x0 (1)
r1 через 100 дней после x0 (2)
T = 220 дней
(1)
(2)

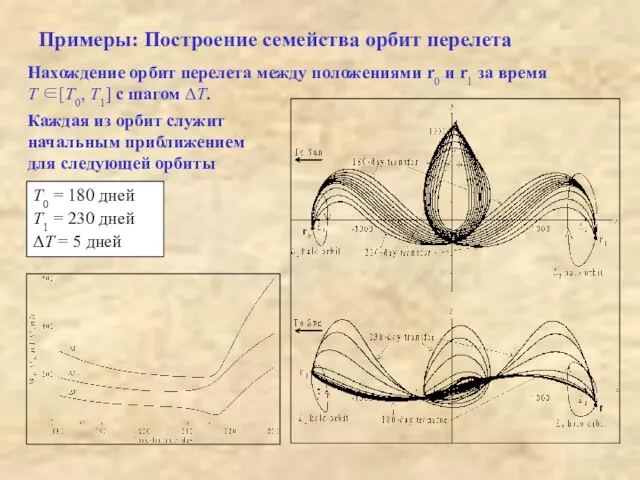
Примеры: Построение семейства орбит перелета
Нахождение орбит перелета между положениями r0 и r1 за время T ∈[T0, T1] с шагом ΔT.
T0 = 180 дней
T1 = 230 дней
ΔT = 5 дней
Каждая из орбит служит начальным приближением для следующей орбиты

Заключение
Опорные орбиты соответствуют перелетам между Землей и точками либрации, однако позволяют находить перелеты между любыми точками и решать другие задачи
Метод может использоваться и в других системах небесных тел с другими моделями движения
Вместо уравнений Хилла могут использоваться точные уравнения задачи трех тел, однако упрощенная модель позволяет находить орбиты без привязки к конкретным датам
Предложенный метод может использоваться как для расчета траекторий полета КА, так и для численного анализа орбит в задаче трех тел