итерационными методами, в которых последовательно, шаг за шагом, производится уточнение начального приближения корня. Итерацией называется совокупность вычислительных операций, приводящих к новому приближенному значению корня. Если каждое последующее значение x(k) (k=1,2,3,…) находится все ближе к точному значению, говорят, что метод сходится. В противном случае метод расходится. Для реализации итерационного процесса должны быть заданы начальное приближение x(0) и точность ε, с которой найти решение уравнения. Условие окончание имеет вид: |x(k)-x(k-1)| ≤ ε
Метод половинного деления ( М П Д )
В этом методе на каждой итерации новое приближение определяется как:
x(k)=( a(k-1)+b(k-1) )/2, где к – н о м е р и те р а ц и и.
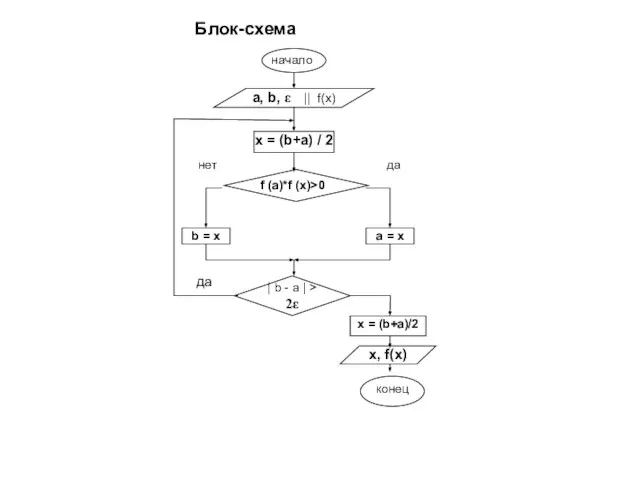
Алгоритм
Заданы функция f(x), отрезок [a(0),b(0)], точность ε. Пусть k=1.
В ы ч и с л я е м приближение x(k)=(a(k-1)+b(k-1)) / 2
О п р е д е л я е м новый отрезок [a(k),b(k)]. Проверяем, если f(a(k-1))*f(x(k))>0, то a(k)=x(k) и b(k)=b(k-1) (остается прежним), иначе b(k)=x(k) и a(k) -остается прежним.
П р о в е р я е м условие окончания, если |b(k)-a(k)| ≤·2ε, то за ответ принимаем значение равное x=(a(k)+b(k))/2 и переходим на пункт 5, иначе k=k+1 и переходим на пункт 2.
В ы в о д x и f(x).

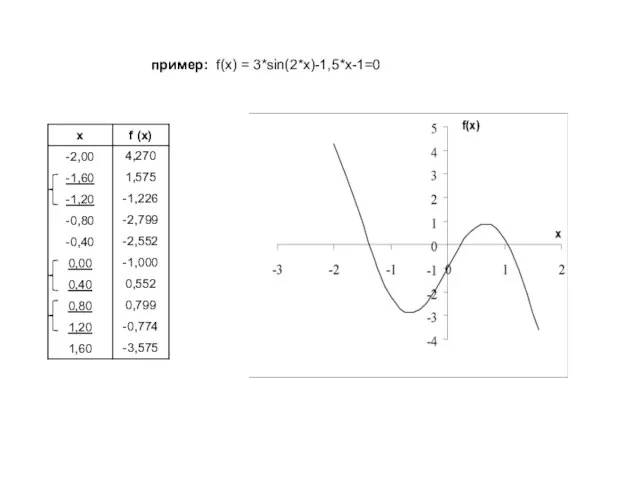

![Уточнение корня на отрезке [a,b], в котором локализован только один корень, осуществляется](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/379604/slide-4.jpg)



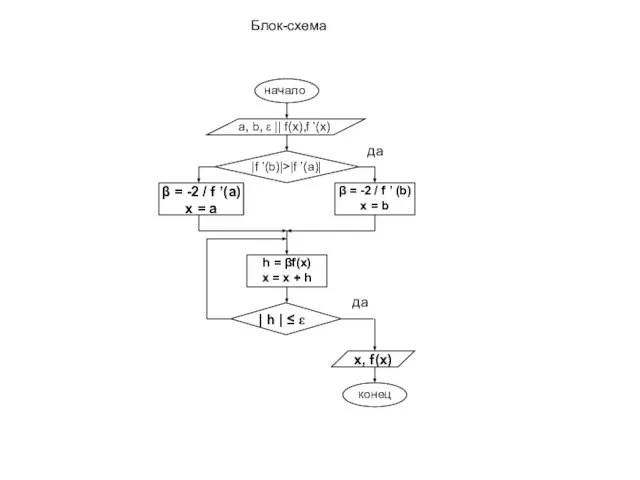
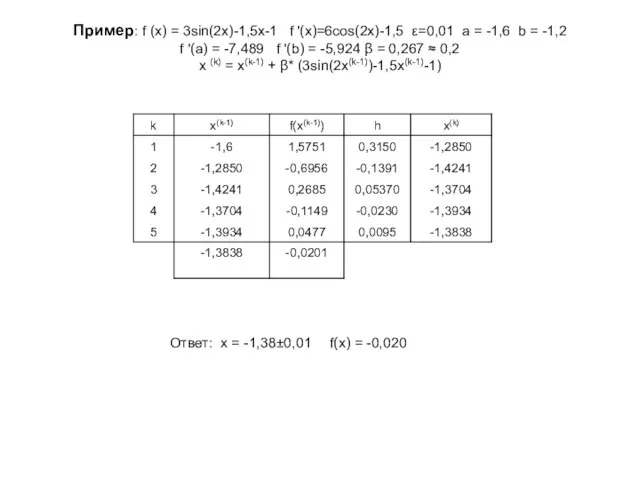

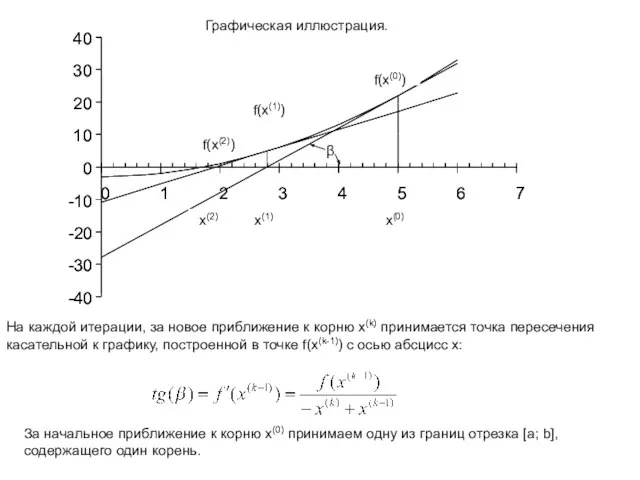
![Алгоритм метода Ньютона Заданы функция f(x) отрезок [a;b] и точность ε. За](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/379604/slide-14.jpg)


 1С-Битрикс Корпоративный портал 10.0 – 10.5
1С-Битрикс Корпоративный портал 10.0 – 10.5 Presentation Title
Presentation Title  Заседание ученого советаПОИПКРО
Заседание ученого советаПОИПКРО СОЦИАЛЬНЫЙ ПРОЕКТ «Там на ухоженных дорожках»
СОЦИАЛЬНЫЙ ПРОЕКТ «Там на ухоженных дорожках» Цель, Процесс, Результат
Цель, Процесс, Результат Гражданское право РФ. Право собственности и иные вещные права
Гражданское право РФ. Право собственности и иные вещные права Энергосбережение в нашей жизни УО «ВГПЛ1 машиностроения им. М.Ф.Шмырева» http://vgpl-1.iatp.by. - презентация
Энергосбережение в нашей жизни УО «ВГПЛ1 машиностроения им. М.Ф.Шмырева» http://vgpl-1.iatp.by. - презентация Интегрированное занятие « Математика + история»
Интегрированное занятие « Математика + история» Тестовые задания
Тестовые задания 3_Биологическая роль воды
3_Биологическая роль воды Презентация на тему Умножение одночлена на многочлен
Презентация на тему Умножение одночлена на многочлен  Иван Сергеевич Тургенев. Начало творческого пути писателя
Иван Сергеевич Тургенев. Начало творческого пути писателя Геометрическая абстракция
Геометрическая абстракция Угол. Сравнение углов. Биссектриса угла
Угол. Сравнение углов. Биссектриса угла Конфликты в семье
Конфликты в семье Вот он цветочек аленький
Вот он цветочек аленький Итоги 2003/2004 учебного года и задачи кафедр по повышению качества подготовки специалистов в новом учебном году Б.Е.Ды
Итоги 2003/2004 учебного года и задачи кафедр по повышению качества подготовки специалистов в новом учебном году Б.Е.Ды Витамин D
Витамин D Профессия Повар-кондитер
Профессия Повар-кондитер Неделя английского языка2011-2012
Неделя английского языка2011-2012 История математической логики
История математической логики Япония 11 класс
Япония 11 класс Склады и пункты приема поставок
Склады и пункты приема поставок Информационно-аналитический проект: Сто дней
Информационно-аналитический проект: Сто дней Тех. задание
Тех. задание Возможности развития познавательной мотивации учащихся.
Возможности развития познавательной мотивации учащихся. Николай Константинович Рерих (874 - 1947)
Николай Константинович Рерих (874 - 1947) Внешняя память компьютера
Внешняя память компьютера