Содержание
- 2. Знать какие неравенства называются неравенствами второй степени с одной переменной. Уметь решать неравенства второй степени с
- 3. 1. Выражение какого вида называется квадратным трёхчленом? 2. Что надо сделать, чтобы найти корни квадратного трёхчлена?
- 4. Как называется функция вида у = ах2 +вх + с ? Квадратичной 2. Что является графиком
- 5. Определение: Неравенства вида ах2 + вх + с > 0 и ах2 + вх + с
- 6. 1. Найдем корни квадратного трехчлена: х2 - 7х + 10 = 0 Д = 9 х1=
- 7. 2. Рассмотрим функцию: у = х2 - 7х + 10 Графиком этой функции является - парабола
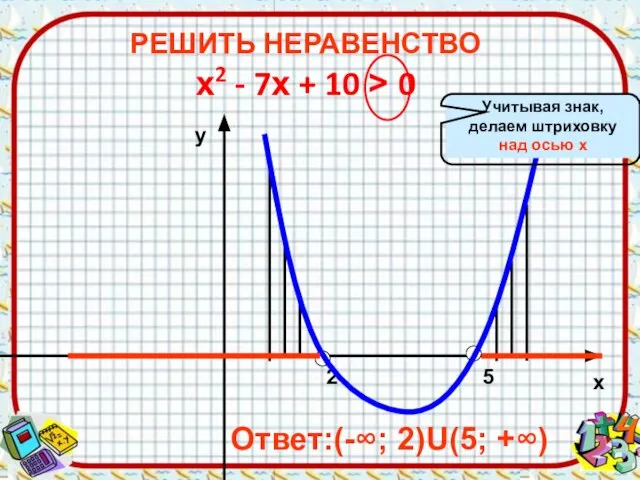
- 8. 2 5 х у Ответ:(-∞; 2)U(5; +∞) РЕШИТЬ НЕРАВЕНСТВО х2 - 7х + 10 > 0
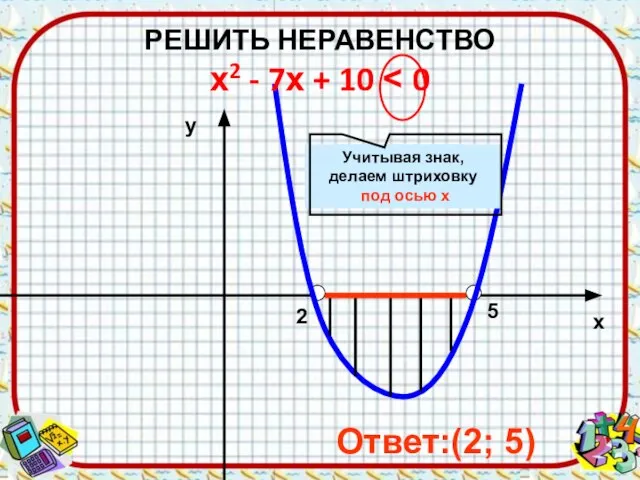
- 9. 2 5 х у Ответ:(2; 5) РЕШИТЬ НЕРАВЕНСТВО х2 - 7х + 10 Учитывая знак, делаем
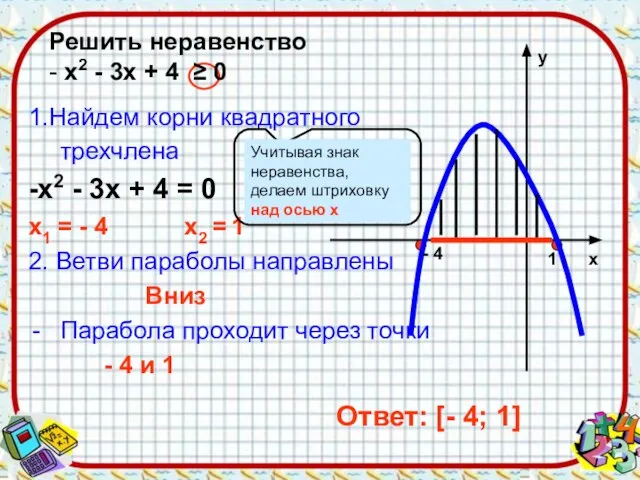
- 10. 1.Найдем корни квадратного трехчлена -х2 - 3х + 4 = 0 х1 = - 4 х2
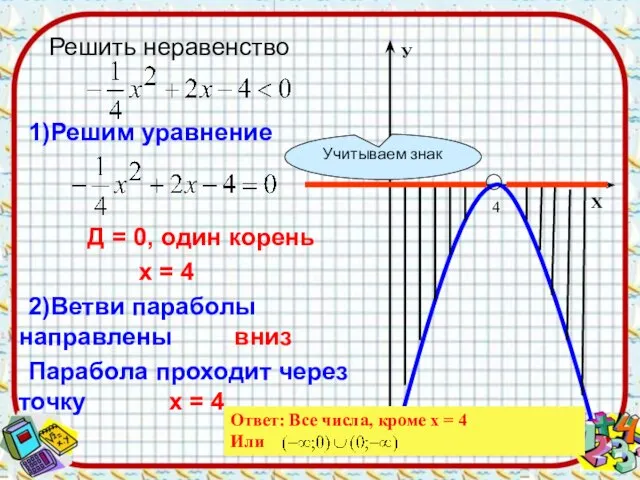
- 11. 1)Решим уравнение Д = 0, один корень х = 4 2)Ветви параболы направлены вниз Парабола проходит
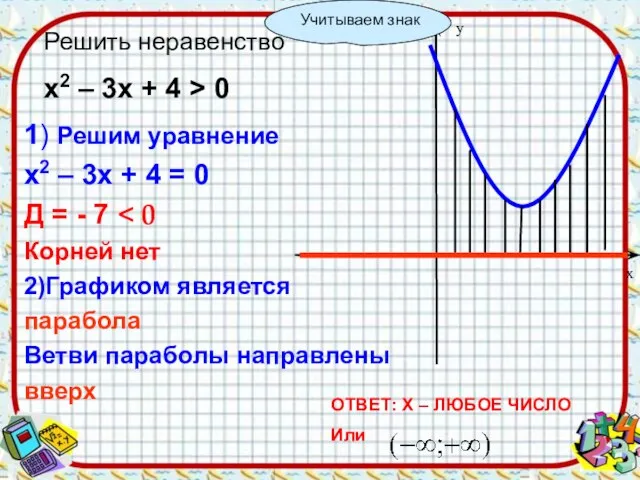
- 12. 1) Решим уравнение х2 – 3х + 4 = 0 Д = - 7 Корней нет
- 13. План решения неравенств второй степени Чтобы решить неравенства вида ах2 + вх + с > 0
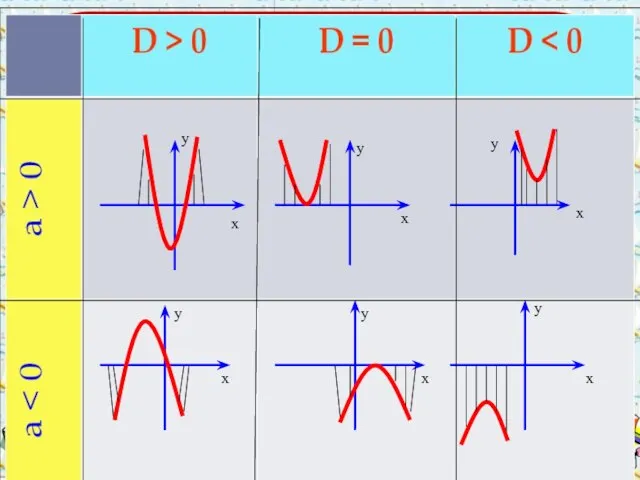
- 14. х у у х у х у х у х у х
- 16. Скачать презентацию







 Курсовая работа по дисциплине “Математические методы” на тему “Игры с природой”
Курсовая работа по дисциплине “Математические методы” на тему “Игры с природой” Terex RS446 Регенератор / Стабилизатор
Terex RS446 Регенератор / Стабилизатор Определи падеж.
Определи падеж. Определение количества информации
Определение количества информации ОЗК и противогазы. Назначение, устройство и принцип действия
ОЗК и противогазы. Назначение, устройство и принцип действия Русский терем
Русский терем Пижамные брюки. Обработка верхнего среза пижамных брюк притачным поясом
Пижамные брюки. Обработка верхнего среза пижамных брюк притачным поясом Муниципальное дошкольное образовательное учреждение «Детский сад № 47» Рожкова Галина Ивановна Попеляева Галина Константиновна
Муниципальное дошкольное образовательное учреждение «Детский сад № 47» Рожкова Галина Ивановна Попеляева Галина Константиновна Исследование прибрежных преобразователей энергии волн
Исследование прибрежных преобразователей энергии волн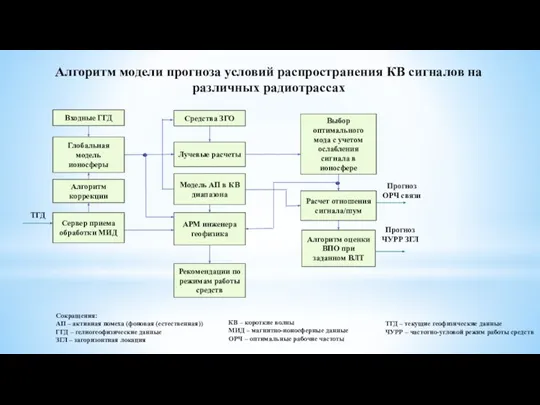 Алгоритм модели прогноза условий распространения КВ сигналов на различных радиотрассах
Алгоритм модели прогноза условий распространения КВ сигналов на различных радиотрассах История Владимирского края
История Владимирского края Педагогический анализ работы МОУ «Казначеевская СОШ» за 2007-2008 учебный год.
Педагогический анализ работы МОУ «Казначеевская СОШ» за 2007-2008 учебный год. Делимость чисел
Делимость чисел Сетевые ОС
Сетевые ОС ПРИМЕНЕНИЕ ОНТОЛОГИЙ ПРИ ПОСТРОЕНИИ ТЕСТОВ ДЛЯ ПРОВЕРКИ УРОВНЯ ПОДГОТОВКИ ОБУЧАЕМЫХ
ПРИМЕНЕНИЕ ОНТОЛОГИЙ ПРИ ПОСТРОЕНИИ ТЕСТОВ ДЛЯ ПРОВЕРКИ УРОВНЯ ПОДГОТОВКИ ОБУЧАЕМЫХ Тема:«Бросание мяча под определёнными углами к горизонту для попадания в площадную цель»
Тема:«Бросание мяча под определёнными углами к горизонту для попадания в площадную цель» Компания ТОО GFcom. Оптово-розничная компания, входящая в список лидеров по продаже автокомпонентов на территории Казахстана
Компания ТОО GFcom. Оптово-розничная компания, входящая в список лидеров по продаже автокомпонентов на территории Казахстана Цветовые наименования в творчестве
Цветовые наименования в творчестве Риск и промышленная безопасность
Риск и промышленная безопасность  ЛЮДИ
ЛЮДИ Приобретение гражданства в России1
Приобретение гражданства в России1 AOUT/May01 Влияние качества смазочных материалов на агрегаты гидросистем.
AOUT/May01 Влияние качества смазочных материалов на агрегаты гидросистем. Выполнение болевых приёмов при подходе к правонарушителю спереди
Выполнение болевых приёмов при подходе к правонарушителю спереди ?
? Природные достопримечательности Румынии
Природные достопримечательности Румынии  Мировой посредник
Мировой посредник Автоматизация звука Р в 2-3х сложных словах
Автоматизация звука Р в 2-3х сложных словах Почвогрунты для улучшения качества почвы
Почвогрунты для улучшения качества почвы