Содержание
- 2. В 7 классе на уроках геометрии мы познакомились с задачами на построение. В учебниках предложен один
- 3. В геометрии выделяют задачи на построение, которые можно решить только с помощью двух инструментов: циркуля и
- 4. Основные этапы решения задачи на построение 1 АНАЛИЗ 2. ПОСТРОЕНИЕ 3. ДОКАЗАТЕЛЬСТВО 4. ИССЛЕДОВАНИЕ В том
- 5. Условные обозначения ∠ - знак угла окр(О;г) - окружность с центром в точке О и радиусом
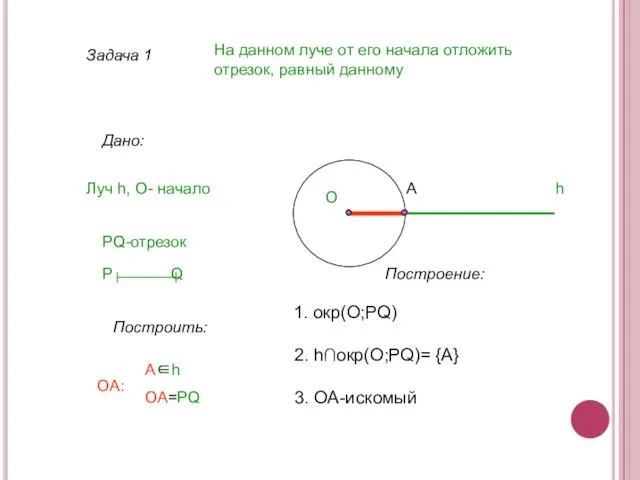
- 6. Задача 1 На данном луче от его начала отложить отрезок, равный данному Дано: Луч h, О-
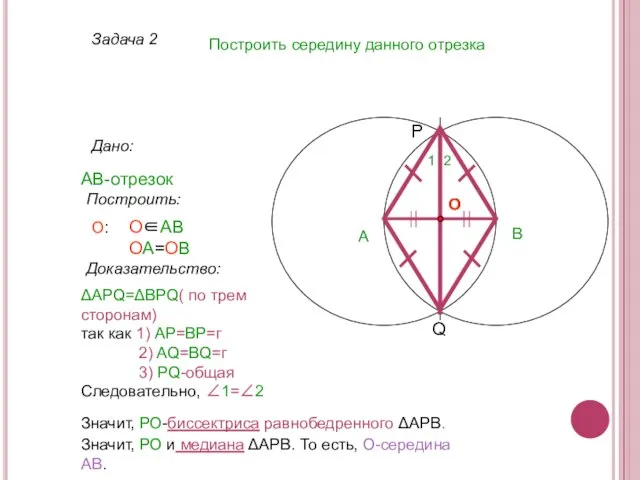
- 7. Задача 2 Построить середину данного отрезка Дано: АВ-отрезок А Построить: О∈АВ ОА=ОВ О: Построение: 1. окр(А
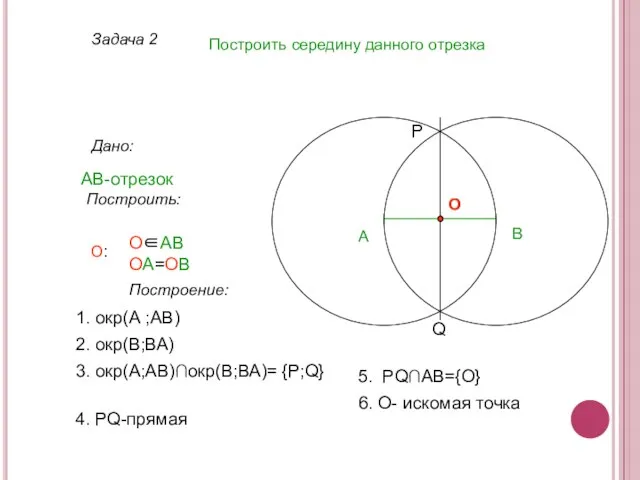
- 8. Задача 2 Построить середину данного отрезка Дано: АВ-отрезок А Построить: О∈АВ ОА=ОВ О: P Q О
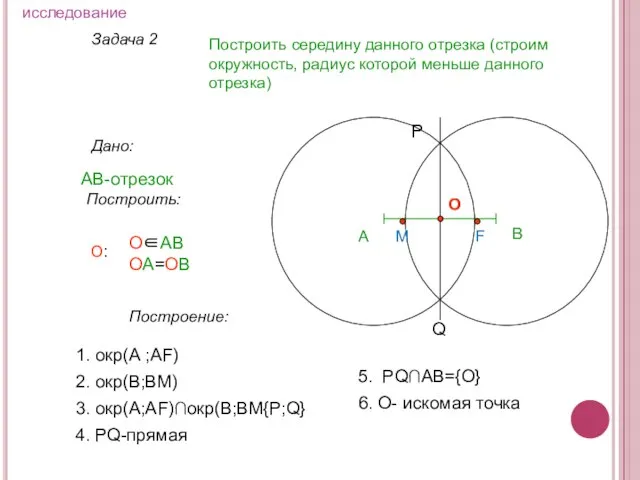
- 9. Задача 2 Построить середину данного отрезка (строим окружность, радиус которой меньше данного отрезка) Дано: АВ-отрезок А
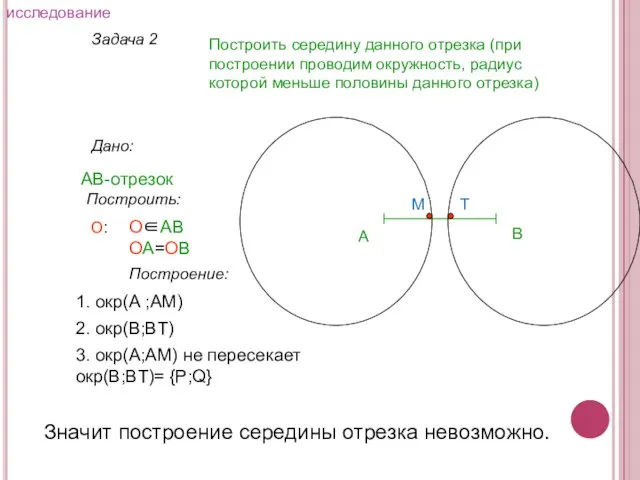
- 10. Задача 2 Построить середину данного отрезка (при построении проводим окружность, радиус которой меньше половины данного отрезка)
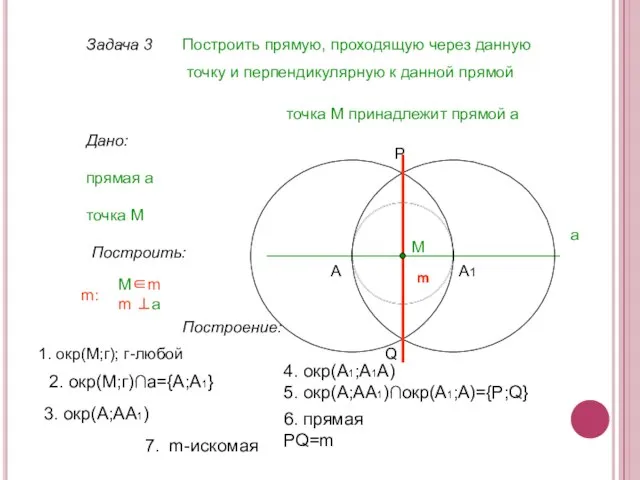
- 11. Задача 3 Построить прямую, проходящую через данную точку и перпендикулярную к данной прямой Дано: прямая а
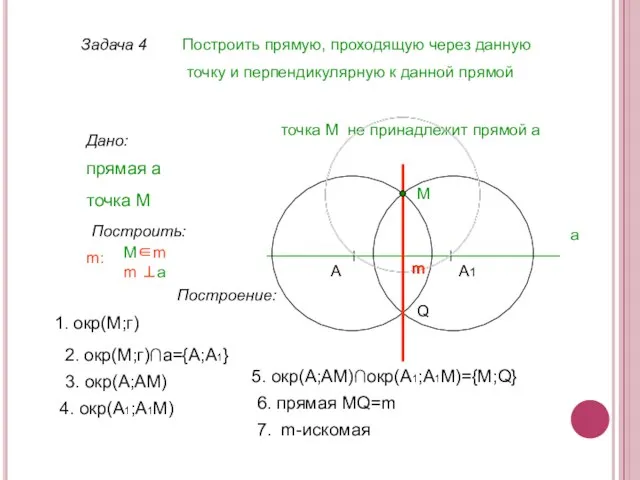
- 12. Задача 4 Построить прямую, проходящую через данную точку и перпендикулярную к данной прямой Дано: прямая а
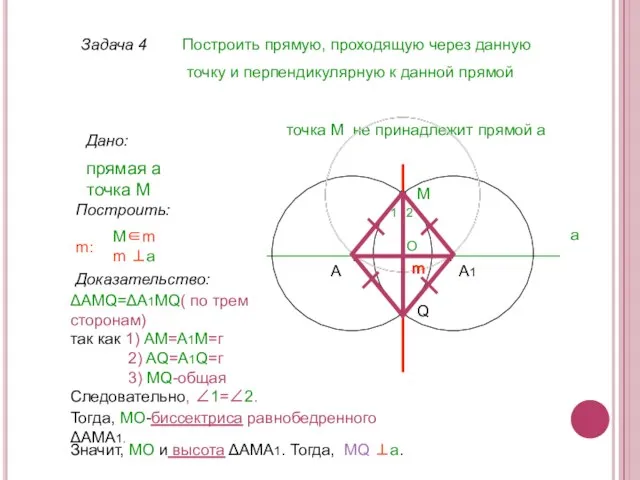
- 13. Задача 4 Построить прямую, проходящую через данную точку и перпендикулярную к данной прямой Дано: прямая а
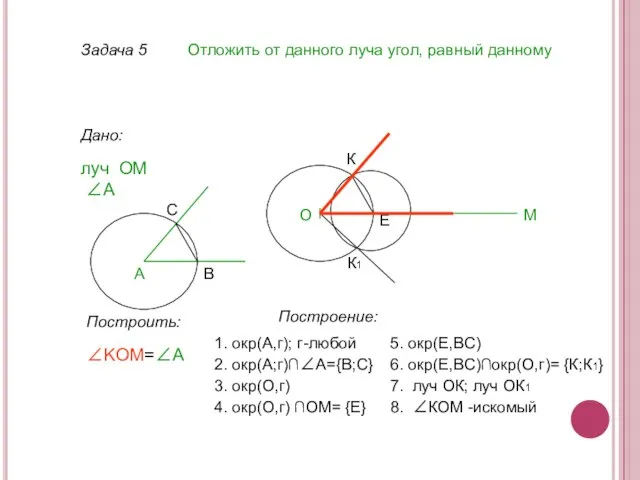
- 14. Задача 5 Отложить от данного луча угол, равный данному Дано: луч ОМ О М ∠А А
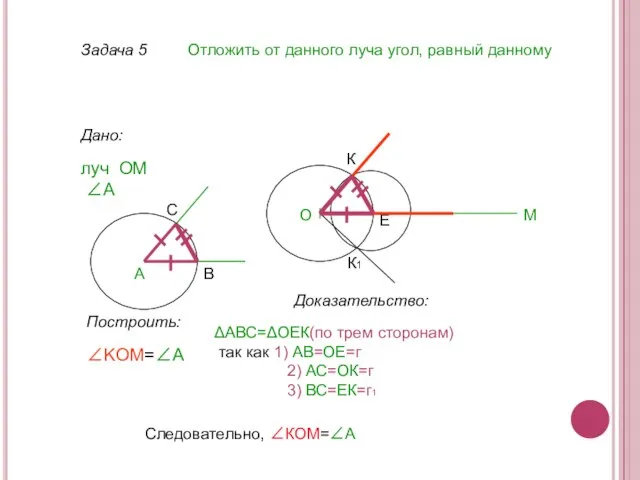
- 15. Задача 5 Отложить от данного луча угол, равный данному Дано: луч ОМ О М ∠А А
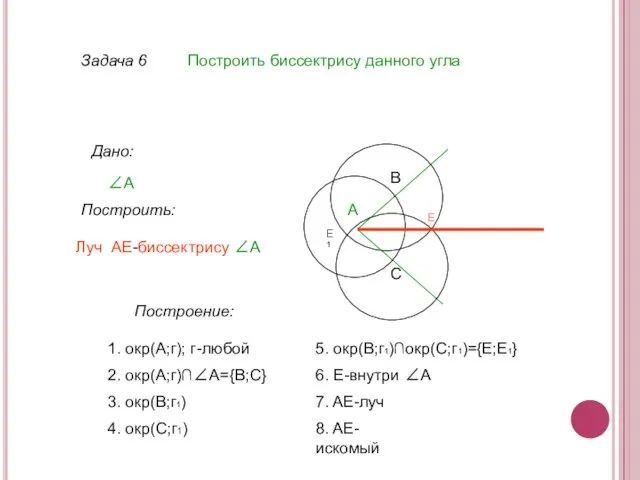
- 16. Задача 6 Построить биссектрису данного угла Дано: ∠А Построить: Построение: А 1. окр(А;г); г-любой Луч AE-биссектрису
- 18. Скачать презентацию




 Красное-черное. Творческая работа
Красное-черное. Творческая работа Презентация на тему Олимпийский огонь
Презентация на тему Олимпийский огонь Предиктивная аналитика рисков в системе закупок
Предиктивная аналитика рисков в системе закупок А если одного предложения мало?
А если одного предложения мало? 20171102_nauki_o_prirode
20171102_nauki_o_prirode Учреждение образования «Белорусский государственный университет физической культуры»
Учреждение образования «Белорусский государственный университет физической культуры» Derecho inmobiliario Power Point (Protección posesión y propiedad)
Derecho inmobiliario Power Point (Protección posesión y propiedad) Родительское собрание
Родительское собрание Презентация на тему Неклеточные формы жизни вирусы (10 класс)
Презентация на тему Неклеточные формы жизни вирусы (10 класс) ПРОГРАММА «ТРУДОВАЯ СЛАВА РОССИИ» Инициатор: Автономная некоммерческая организация содействия повышению престижа труда и социа
ПРОГРАММА «ТРУДОВАЯ СЛАВА РОССИИ» Инициатор: Автономная некоммерческая организация содействия повышению престижа труда и социа Урок 13.БАЙКИ ЕЗОПА
Урок 13.БАЙКИ ЕЗОПА Айрис фолдинг (радужное складывание)
Айрис фолдинг (радужное складывание) ПОЛЬ ГОГЕН
ПОЛЬ ГОГЕН Противодействие коррупции в США
Противодействие коррупции в США Буква Я
Буква Я Автомобильный транспорт
Автомобильный транспорт  Золотопромышленность в Енисейской губернии
Золотопромышленность в Енисейской губернии Ученик года - 2016
Ученик года - 2016 Фотография. Что можно назвать фотографией?
Фотография. Что можно назвать фотографией? Vocabulary presentation
Vocabulary presentation Молоко и его свойства
Молоко и его свойства Социокультурные детерминанты развития и торможения исследовательского поведения
Социокультурные детерминанты развития и торможения исследовательского поведения Когнитивная психология
Когнитивная психология Понятие административного права
Понятие административного права Половое и бесполое размножение. Обобщение
Половое и бесполое размножение. Обобщение Pervy_urok_Moya_istoria
Pervy_urok_Moya_istoria Применение SCAD Office для расчета сооружений сложной геометрической формы на сейсмические воздействия(нормы и опыт расчетов)
Применение SCAD Office для расчета сооружений сложной геометрической формы на сейсмические воздействия(нормы и опыт расчетов) Проведение индустриализации в СССР: методы, результаты, цена. Коллективизация в СССР: причины, методы проведения, итоги
Проведение индустриализации в СССР: методы, результаты, цена. Коллективизация в СССР: причины, методы проведения, итоги