Слайд 2Способы решения
По определению
Исходя из геометрического смысла
По общей схеме
Использование

специальных соотношений и свойств модуля
Слайд 4Исходя из геометрического смысла
– расстояние на числовой прямой от точки

0 до точки
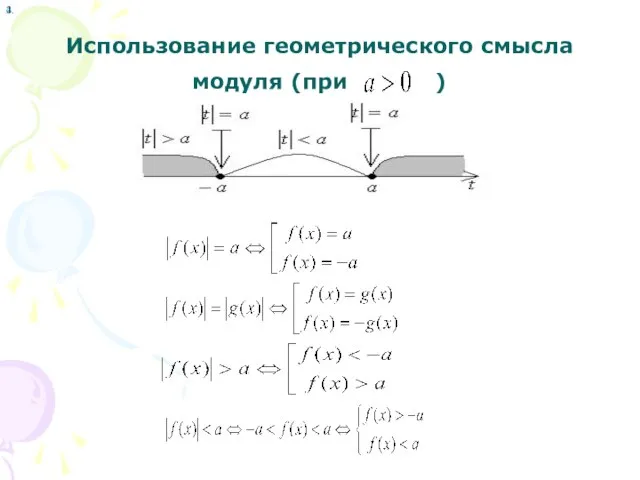
Слайд 5Использование геометрического смысла модуля (при )
1.
2.
3.
4.
Слайд 6По общей схеме
Найти ОДЗ
Найти нули всех подмодульных функций
Отметить нули на ОДЗ

и разбить ОДЗ на интервалы
Найти решение в каждом интервале ( и проверить, входит ли решение в этот интервал)
Слайд 7Использование специальных соотношений и свойств модуля
2.
3.
4.
5.
1.

Слайд 86.
7.
8.
9.
1 свойство:
2 свойство:
3 свойство
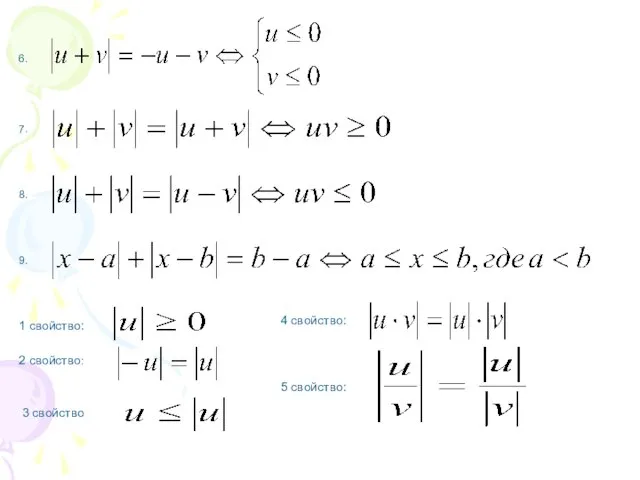
Слайд 96 свойство:
7 свойство:
8 свойство:
9 свойство:
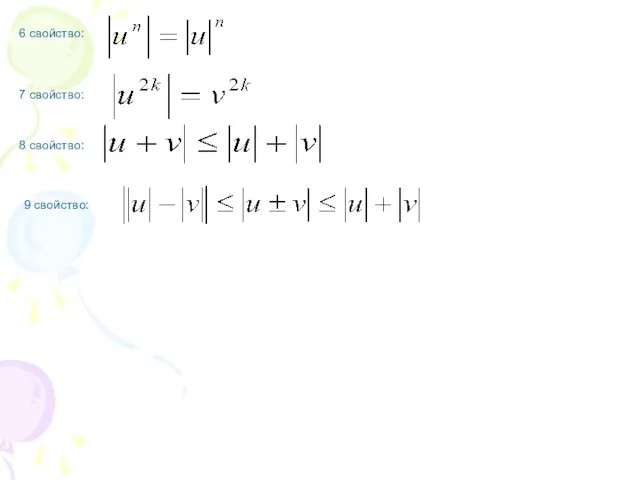
Слайд 10Графические приемы решения задач с параметрами
Применение параллельного переноса
Применение поворота
Применение гомотетии

и сжатия к прямой
Параметр как равноправная переменная на плоскости
Слайд 11Применение параллельного переноса
1. Сколько корней имеет уравнение
, в зависимости от

значений параметра
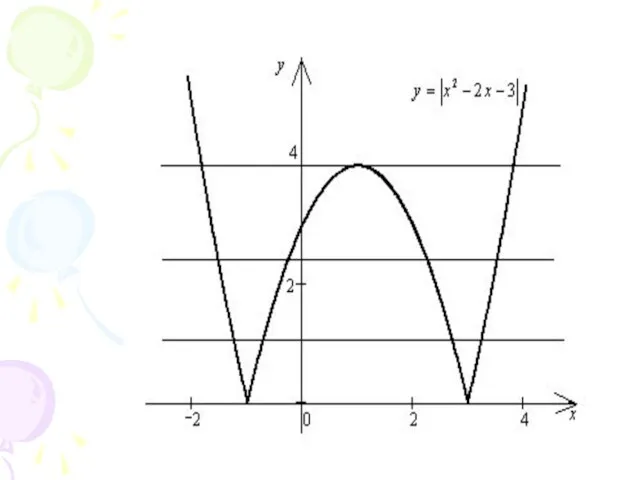
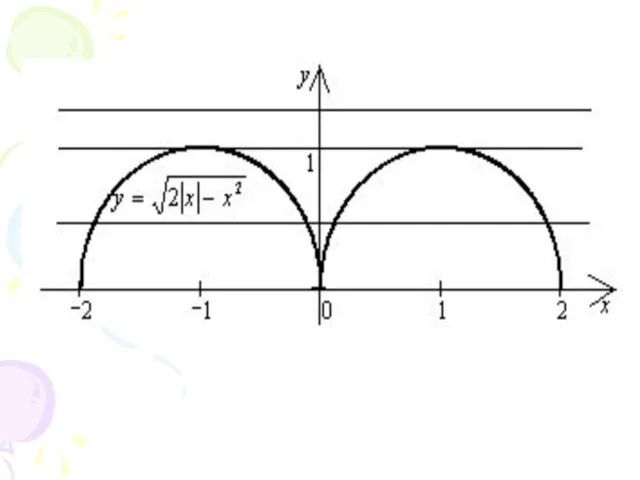
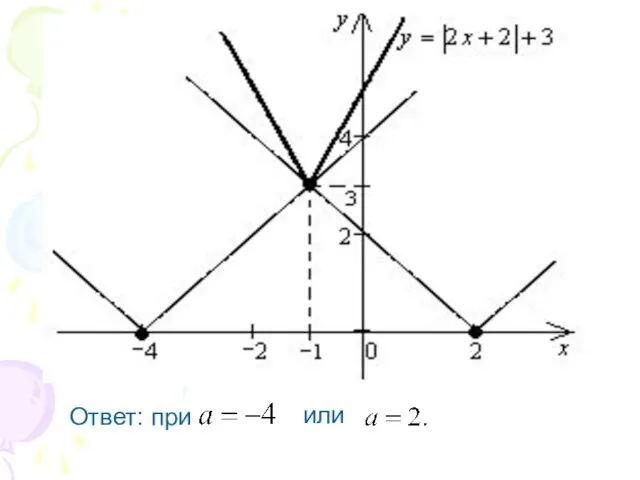
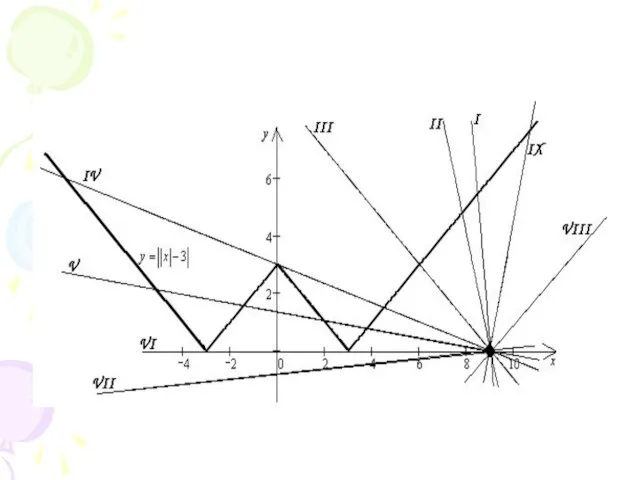
Слайд 12Построим в одной системе координат
графики функций
и .

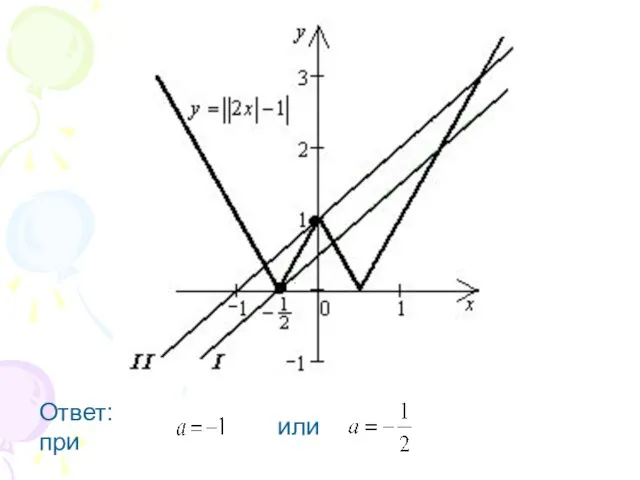
Слайд 14Ответ: при корней нет;
при или два корня;
при четыре корня;
при

три корня.
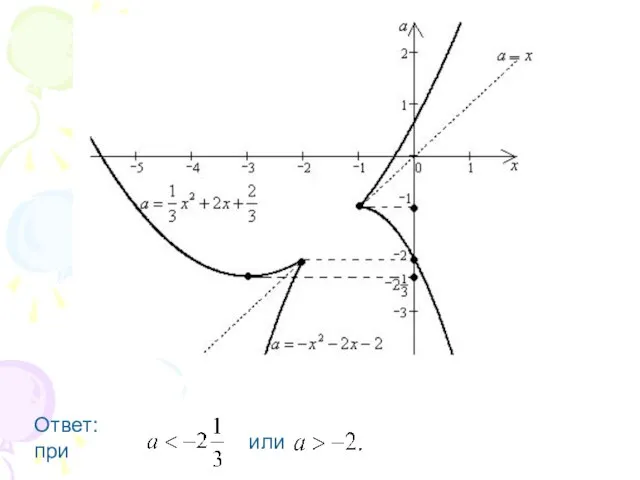
Слайд 152. Сколько корней имеет уравнение
, в зависимости от значений параметра ?

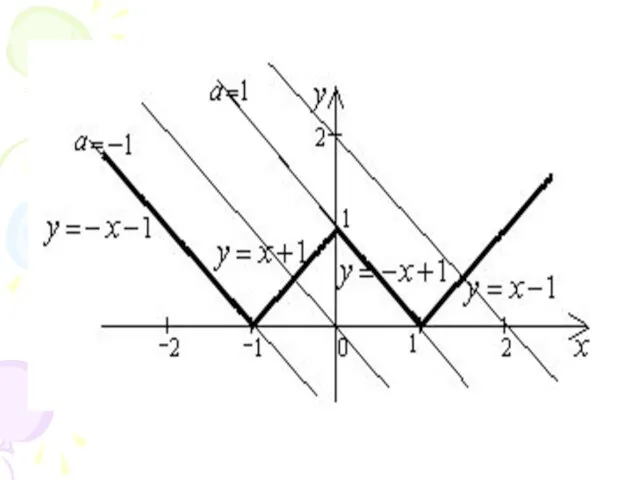
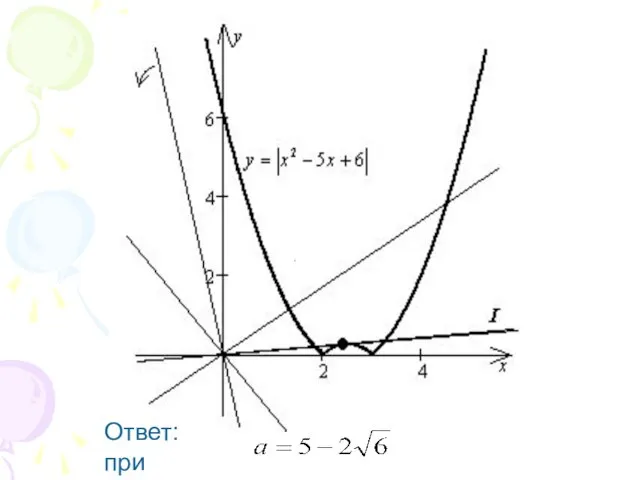
Слайд 16Построим в одной системе координат
графики функций и .

Слайд 19Ответ: при или корней нет;
при два корня;
при три корня;
при

четыре корня.
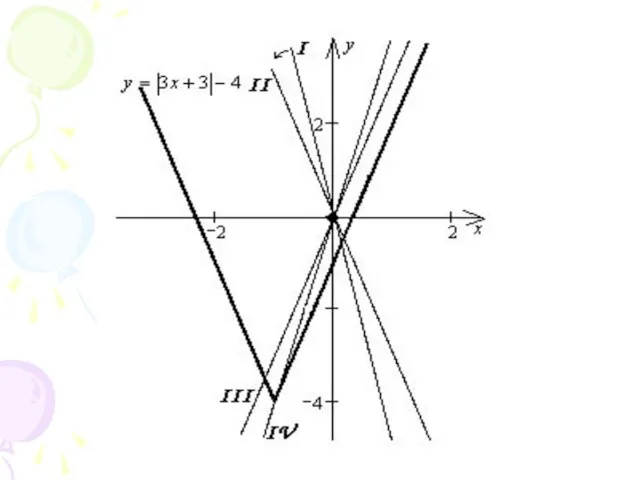
Слайд 203. При каких значениях параметра уравнение
имеет ровно три решения?

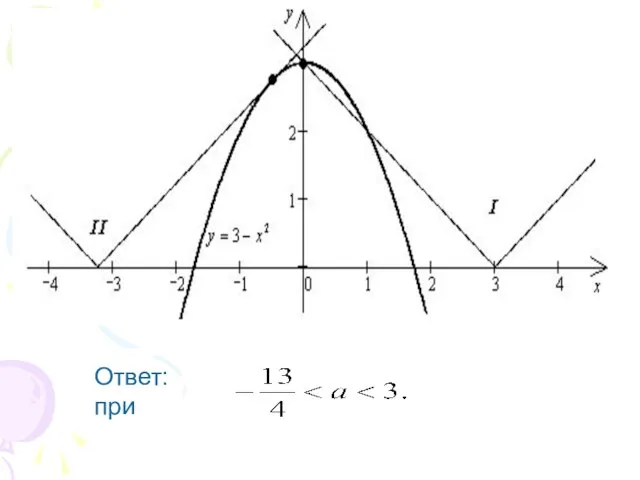
Слайд 24Ответ: при нет решений;
при ;
при .

Слайд 255. При каких значениях параметра
неравенство имеет хотя бы одно
отрицательное решение?

Слайд 276. При каких значениях параметра
уравнение
имеет единственное решение?

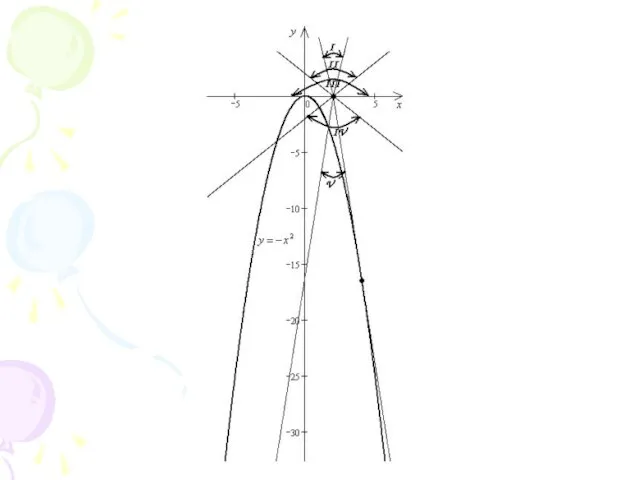
Слайд 29Применение поворота
1. При каких значениях параметра уравнение
имеет ровно три решения?

Слайд 343. Сколько корней имеет уравнение
в зависимости от значений параметра ?

Слайд 36Ответ: при один корень;
при два корня; при три корня;
при четыре

корня; при два корня; при корней нет; при один корень.
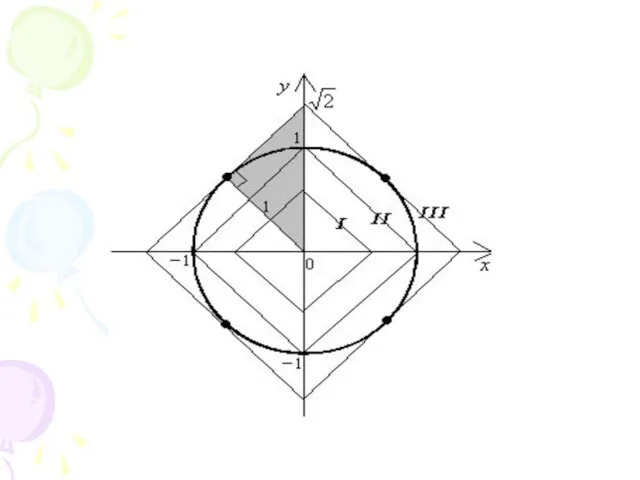
Слайд 37Применение гомотетии и сжатия к прямой
Сколько решений имеет система
уравнений ?

Слайд 39Ответ: при
решений нет; при
четыре решения; при
восемь

решений; при
четыре решения; при
решений нет.
Слайд 402. Сколько решений имеет уравнение

Слайд 41Построим в одной системе координат графики
функций
и . Вторая функция задает на

плоскости семейство «уголков» с вершиной в точке (2;0).
Слайд 43Ответ: при
нет решений; при
один корень; при
два

корня; при
три корня; при
четыре корня.
Слайд 44Параметр как равноправная переменная на плоскости
При каких значениях параметра
уравнение

имеет ровно три решения?
Слайд 45Данное уравнение равносильно совокупности уравнений

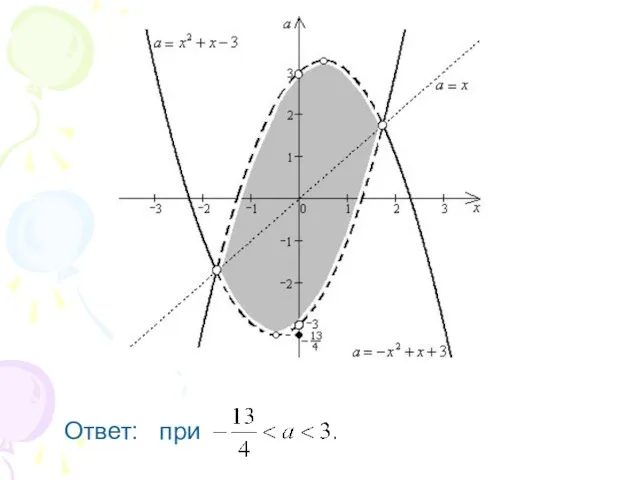
Слайд 472. При каких значениях параметра уравнение
имеет ровно два решения?

Слайд 48Данное уравнение равносильно совокупности

Слайд 51Ответ: при
нет решений; при
; при
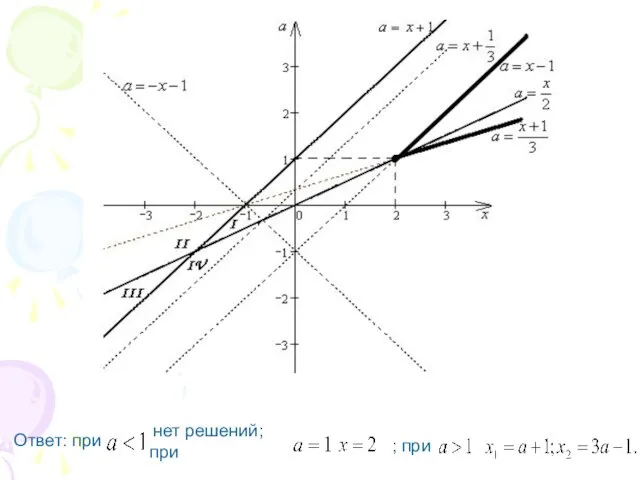
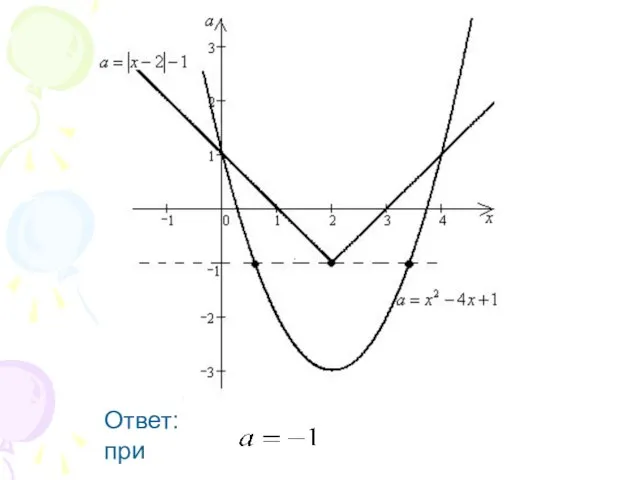
Слайд 524. При каких значениях параметра уравнение
имеет ровно три решения?

Слайд 555. При каких значениях параметра неравенство
имеет хотя бы одно отрицательное решение?

Слайд 56Данное неравенство равносильно совокупности
Данное неравенство равносильно совокупности

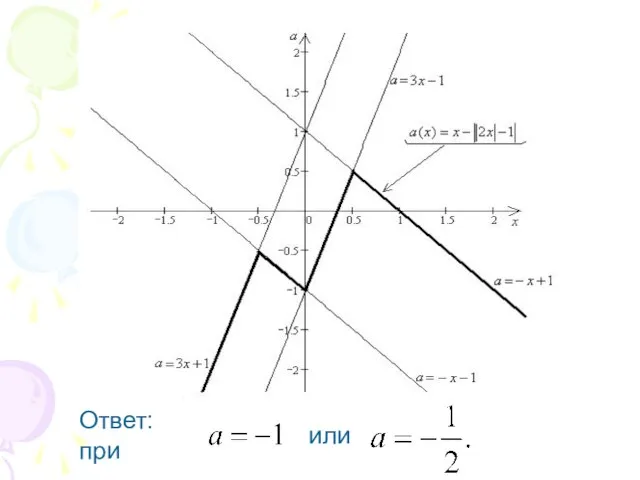
Слайд 585. При каких значениях параметра уравнение имеет единственное решение?

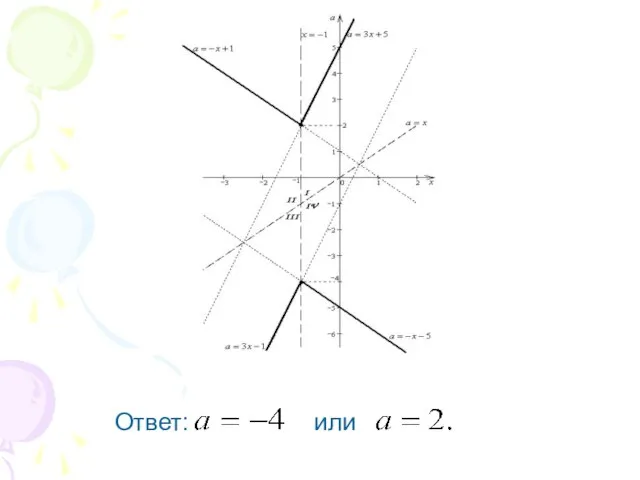
Слайд 606. При каких значениях параметра
уравнение
имеет ровно три решения?







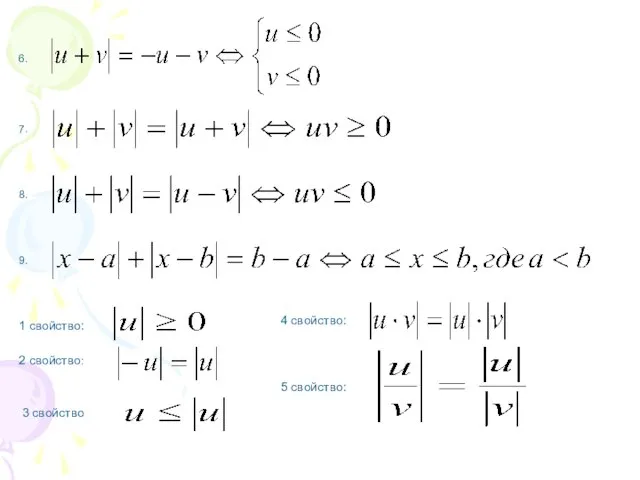
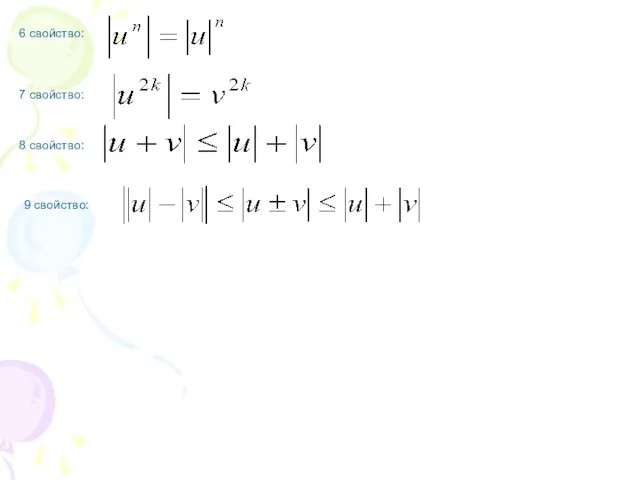






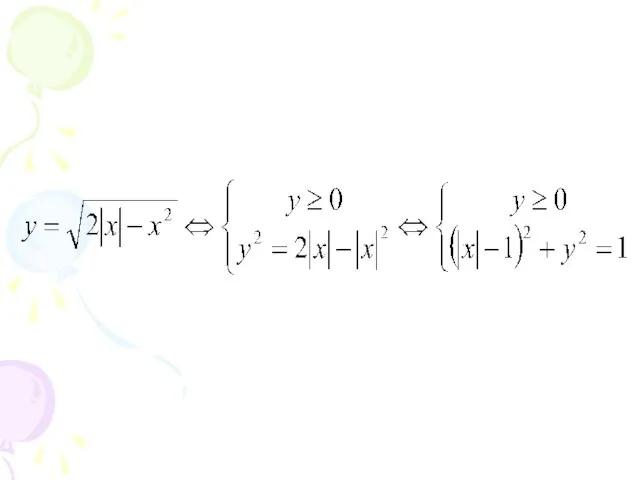








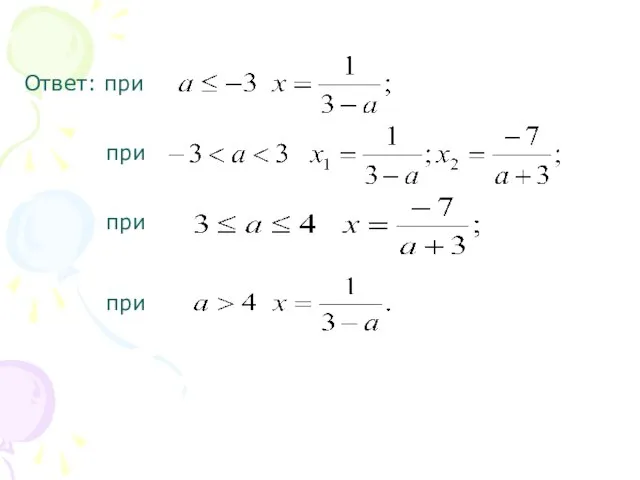



















 Презентация на тему Правила дорожного движения для младших школьников
Презентация на тему Правила дорожного движения для младших школьников Создание Web-сайтов в программе Microsoft FrontPage
Создание Web-сайтов в программе Microsoft FrontPage Викторина по рассказу А.И.Солженицына «Матрёнин двор»
Викторина по рассказу А.И.Солженицына «Матрёнин двор» Берегите слух
Берегите слух Сложение и вычитание Натуральный ряд чисел
Сложение и вычитание Натуральный ряд чисел Возрастная психология и педагогика
Возрастная психология и педагогика Полупроводниковые приборы
Полупроводниковые приборы «Музыка и движение»
«Музыка и движение» Международное сотрудничество РФ в области противодействия коррупции
Международное сотрудничество РФ в области противодействия коррупции Small talk
Small talk  Аукцион "Великобритания"
Аукцион "Великобритания" Темы для докладов
Темы для докладов Бизнес-результаты ППФ страхование жизни
Бизнес-результаты ППФ страхование жизни Формы госудасрства
Формы госудасрства Оптические приборы. Глаз
Оптические приборы. Глаз Литературное развитие
Литературное развитие СОДЕРЖАНИЕ И ПЕРСПЕКТИВЫ ДЕЯТЕЛЬНОСТИ ГОРОДСКОГО НАУЧНОГО ОБЩЕСТВА УЧАЩИХСЯ
СОДЕРЖАНИЕ И ПЕРСПЕКТИВЫ ДЕЯТЕЛЬНОСТИ ГОРОДСКОГО НАУЧНОГО ОБЩЕСТВА УЧАЩИХСЯ Тонкости оформления и изменения трудового договора
Тонкости оформления и изменения трудового договора Особенности формирования штатных расписаний и тарификаций при введении НСОТ для дошкольных учреждений определены Постановление
Особенности формирования штатных расписаний и тарификаций при введении НСОТ для дошкольных учреждений определены Постановление Моисей Яковлевич Гинзбург (1892-1946)
Моисей Яковлевич Гинзбург (1892-1946) Переломы (2 класс)
Переломы (2 класс) История русского языка
История русского языка Право на освіту в Україні
Право на освіту в Україні Лабораторная диагностика нарушений липидного обмена
Лабораторная диагностика нарушений липидного обмена  Формирование гражданской позиции через историческую связь поколений
Формирование гражданской позиции через историческую связь поколений Как повысить ARPU с помощью интеллектуальных BRAS и внедрения платных дополнительных услуг
Как повысить ARPU с помощью интеллектуальных BRAS и внедрения платных дополнительных услуг Учет материально-производственных запасов
Учет материально-производственных запасов Осень в Богородском районе города Москвы
Осень в Богородском районе города Москвы