Содержание
- 2. Пример: х3 – 5 х2 + 8 х – 4 = 0 х3 – 2 х2
- 3. Цель работы: Выявить способы решения уравнения третьей степени. Задачи работы: 1) Познакомиться с историческими фактами, связанными
- 4. На рубеже XV и XVI веков был подытожен опыт решения уравнений третьей степени в одной из
- 5. К 1539 году Кардано заканчивает свою первую книгу целиком посвященную математике « Практика общей арифметики ».
- 6. В 1543 году Кардано и Феррари поехали в Болонью, где дела Наве позволил им познакомиться с
- 7. «Великое искусство» х3 = ах + b (2) х3 + b = ax (3) Кардано решил
- 8. Кардано полностью разобрался и с общим кубическим уравнением х3 + ах2 + bх +с = 0,
- 9. х3 + рх + q = 0 (1) (2)
- 10. Первый пример: Здесь р = 6 и q = -2. Наша формула дает: В школе нас
- 11. Второй пример: . Формула (3) дает: Ответ более громоздок. Это число можно найти приближенно с помощью
- 12. Третий пример: (х + 1)(х + 2)(х - 3) = 0. Сразу видно, что это уравнение
- 13. Экстремумы многочлена третьей степени у = ах2 + bх + с (1) ( ). у =
- 14. Корень квадратного трехчлена является его точкой экстремума тогда и только тогда, когда этот корень – двукратный.
- 15. Теорема 1. Для того, чтобы точка х= была точкой экстремума функции у = ах2+bх +с, необходимо
- 16. Лемма. Пусть дан многочлен третьей степени у = ах3 + bx2 + сх + d. (
- 17. Теорема 2. Для того чтобы точка х = была точкой экстремума функции у = ах3 +
- 18. Теорема 3.(достаточные условия максимума и минимума). Пусть функция у = ах3 + bx2 + сх +
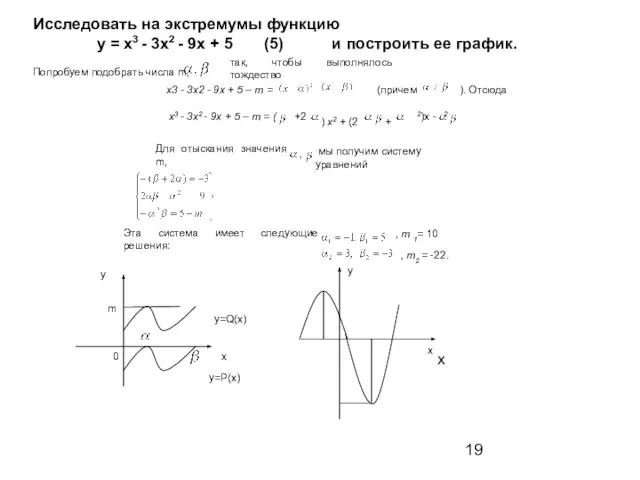
- 19. y=P(x) y=Q(x) у х 0 m Исследовать на экстремумы функцию у = х3 - 3x2 -
- 20. Выводы В процессе работы мы познакомились с историей развития проблемы решения уравнения третьей степени. Теоретическая значимость
- 22. Скачать презентацию
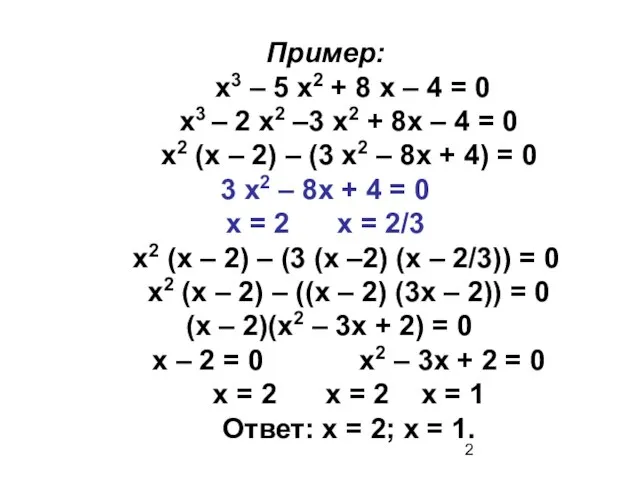






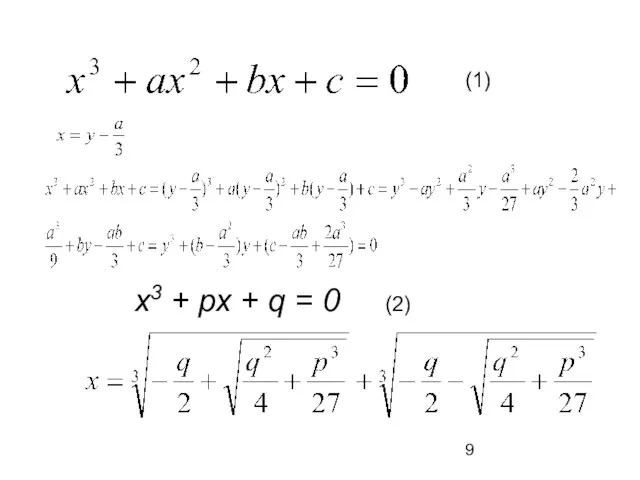










 Висит за окошком Кулёк ледяной, Он полон капели И пахнет весной
Висит за окошком Кулёк ледяной, Он полон капели И пахнет весной Средства регулирования движением поездов
Средства регулирования движением поездов Афины при Перикле
Афины при Перикле Электронная таблица EXCEL
Электронная таблица EXCEL Архетипы
Архетипы УНИДРУА: международный институт по унификации частного права
УНИДРУА: международный институт по унификации частного права Органы чувств
Органы чувств  «Этимологический анализ прозвищ жителей деревень Завражье, Мешково и поселка Судоверфь Судоверфского сельского поселения»
«Этимологический анализ прозвищ жителей деревень Завражье, Мешково и поселка Судоверфь Судоверфского сельского поселения» Новогодние открытки
Новогодние открытки Робототехника. Проект
Робототехника. Проект Балансирующий рынок
Балансирующий рынок Теорема Пифагора
Теорема Пифагора Культура XX века
Культура XX века Деревня Юрьевец
Деревня Юрьевец Wine. The benefits of wine with moderate consumption
Wine. The benefits of wine with moderate consumption Биопсихосоциодуховный подход к профилактике профессионального выгорания психологов
Биопсихосоциодуховный подход к профилактике профессионального выгорания психологов Воздействие высокоскоростных магистралей на окружающую среду
Воздействие высокоскоростных магистралей на окружающую среду Презентация экскурсии в животноводческий комплекс «ИП Каюмов»
Презентация экскурсии в животноводческий комплекс «ИП Каюмов» 07_0___163
07_0___163 каждую неделю около 600 000 слушателей включаются на частоту 100,5 FM каждый день Радио BEST FM слушают около 300 000 человек каждые 15 минут на в
каждую неделю около 600 000 слушателей включаются на частоту 100,5 FM каждый день Радио BEST FM слушают около 300 000 человек каждые 15 минут на в «Белые» в Гражданской войне
«Белые» в Гражданской войне Внедрение здоровьесберегающих технологий
Внедрение здоровьесберегающих технологий Русское искусство 2 пол.19 века
Русское искусство 2 пол.19 века Всегда ли правы мы- родители?
Всегда ли правы мы- родители? Итоги работы отрасли в 2010 году и задачи на 2011 год Глава департамента Елена Борисовна Чеснокова
Итоги работы отрасли в 2010 году и задачи на 2011 год Глава департамента Елена Борисовна Чеснокова Семейные традиции семьи Митрофановых
Семейные традиции семьи Митрофановых HADI – это экспериментальный научный метод исследования, переложенный на бизнес
HADI – это экспериментальный научный метод исследования, переложенный на бизнес ПРОЕКТ КНИЖКА-САМОДЕЛКА «Волшебница Зима» 4 класс
ПРОЕКТ КНИЖКА-САМОДЕЛКА «Волшебница Зима» 4 класс