Содержание
- 2. Правило нахождения процента от числа
- 3. Задача К 150г 10-процентного раствора соли добавили 5-процентный раствор этой же соли и получили 8-процентный раствор.
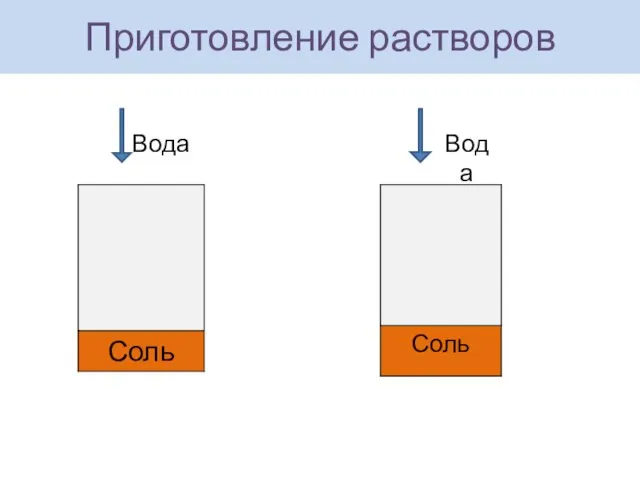
- 4. Приготовление растворов Вода Вода
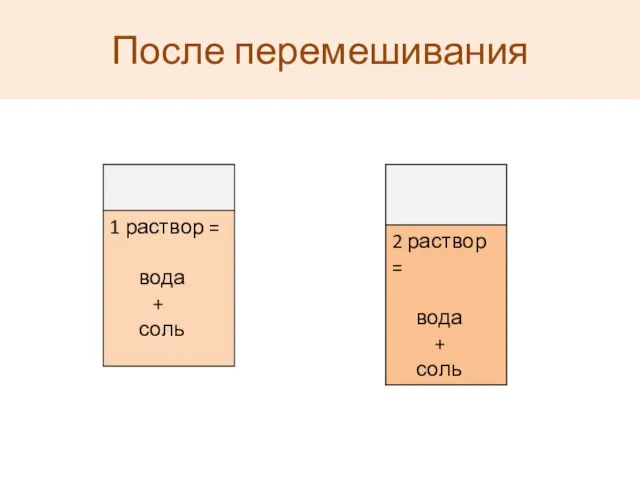
- 5. После перемешивания
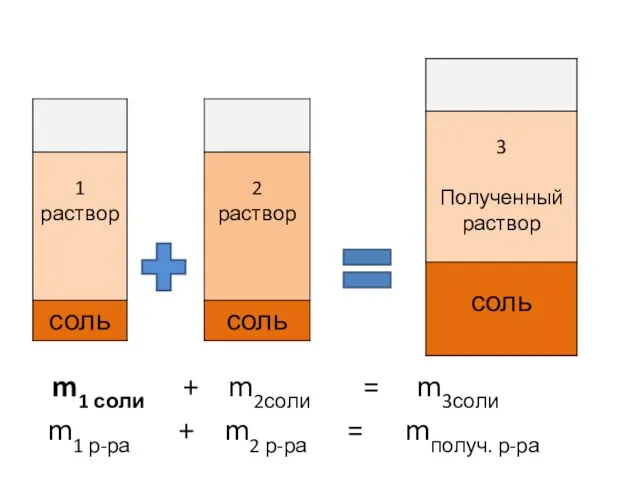
- 6. m1 соли + m2соли = m3соли m1 р-ра + m2 р-ра = mполуч. р-ра
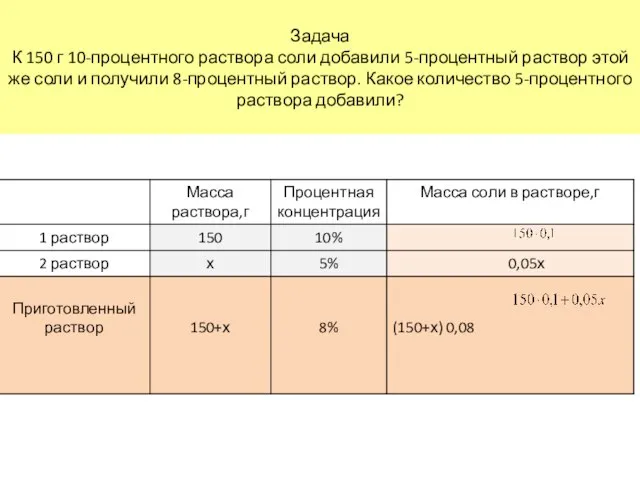
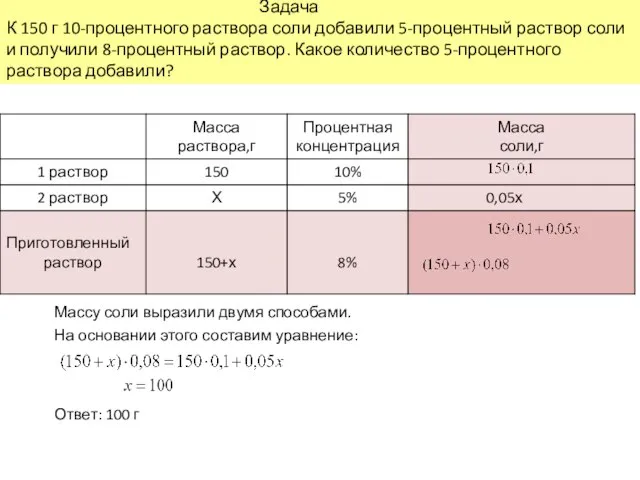
- 7. Задача К 150 г 10-процентного раствора соли добавили 5-процентный раствор этой же соли и получили 8-процентный
- 8. Задача К 150 г 10-процентного раствора соли добавили 5-процентный раствор соли и получили 8-процентный раствор. Какое
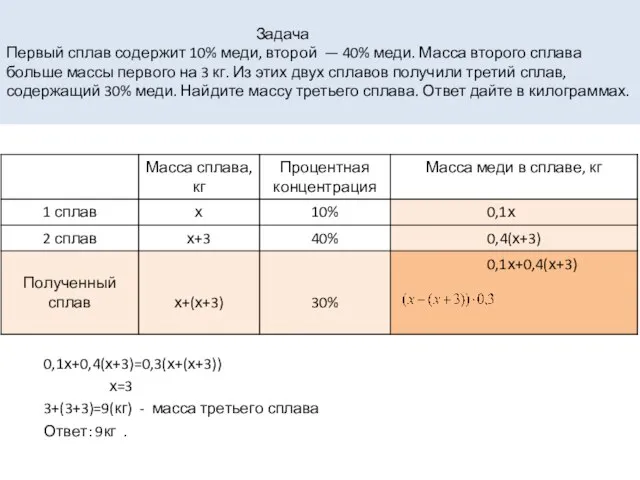
- 9. Задача Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого
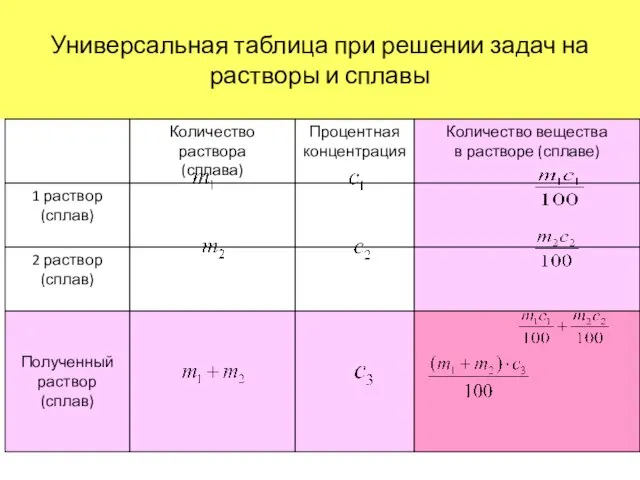
- 10. Универсальная таблица при решении задач на растворы и сплавы
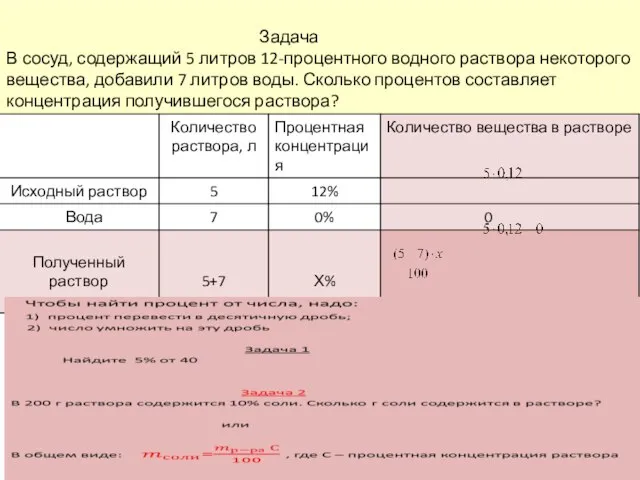
- 11. Задача В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько
- 12. Задача Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19-процентного раствора этого вещества.
- 13. Задача Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов
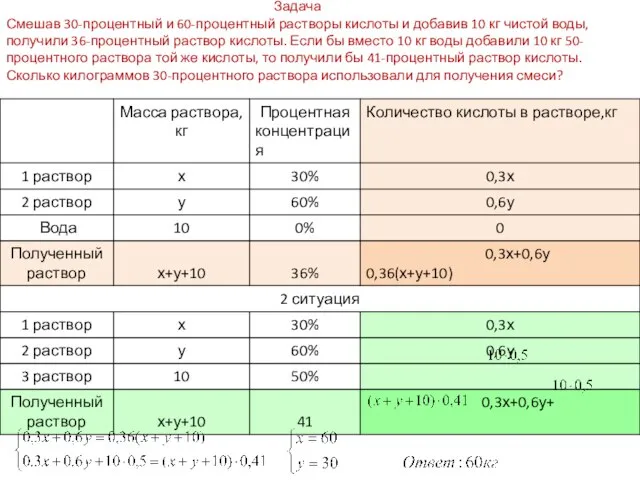
- 14. Задача Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор
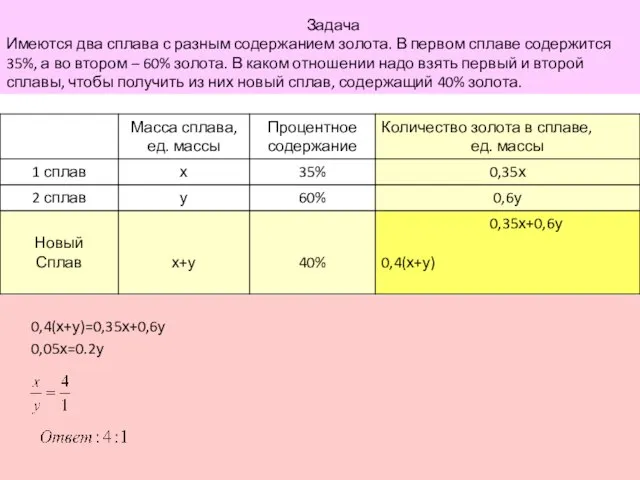
- 15. Задача Имеются два сплава с разным содержанием золота. В первом сплаве содержится 35%, а во втором
- 16. Задачи Имеется два сплава. Первый содержит 5% никеля, второй — 20% никеля. Из этих двух сплавов
- 17. Имеется два сосуда. Первый содержит 100 кг, а второй — 60 кг раствора кислоты различной концентрации.
- 19. Скачать презентацию






 ЖКХ-ПРА-ДК-проекты
ЖКХ-ПРА-ДК-проекты Потребление электроэнергии учениками нашей школы дома
Потребление электроэнергии учениками нашей школы дома Русская эпическая опера. Опера «Князь Игорь» А.Бородин
Русская эпическая опера. Опера «Князь Игорь» А.Бородин Презентация на тему Семейство кошачьих
Презентация на тему Семейство кошачьих Разработка предложений по направлениям развития морских побережий России, обеспечивающих сохранение, реабилитацию и устойчивое
Разработка предложений по направлениям развития морских побережий России, обеспечивающих сохранение, реабилитацию и устойчивое  Презентация на тему Рождество в Германии
Презентация на тему Рождество в Германии СВОЯ ФИНАНСОВАЯ ИГРА ПРОЕКТ
СВОЯ ФИНАНСОВАЯ ИГРА ПРОЕКТ Зарубіжний досвід у сфері соціального страхування з тимчасової втрати працездатності
Зарубіжний досвід у сфері соціального страхування з тимчасової втрати працездатності Построение падающих теней от предметов мебели в угловом интерьере
Построение падающих теней от предметов мебели в угловом интерьере Деньги и инстинкты
Деньги и инстинкты Switzerland
Switzerland Презентация на тему Чарльз дарвин Чарльз Дарвин (1809-1882)
Презентация на тему Чарльз дарвин Чарльз Дарвин (1809-1882)  Дом, в котором я живу
Дом, в котором я живу Предложение фирмы «Проектика» по производству и поставке торгового оборудования ТМ «Доктор Мебелис» - специализированной мебели
Предложение фирмы «Проектика» по производству и поставке торгового оборудования ТМ «Доктор Мебелис» - специализированной мебели  Медицина в искусстве
Медицина в искусстве Буква М
Буква М Педагогические Lookи
Педагогические Lookи Надежность технологической системы
Надежность технологической системы Техника прыжка в высоту перешагивание. Отталкивание
Техника прыжка в высоту перешагивание. Отталкивание Мониторинг ситуации на рынке профессий
Мониторинг ситуации на рынке профессий Василий Шукшин
Василий Шукшин Реостаты 8 класс
Реостаты 8 класс спина болит
спина болит Презентация на тему Импрессионизм в живописи
Презентация на тему Импрессионизм в живописи  20170903_sladkaya_promyshlennost
20170903_sladkaya_promyshlennost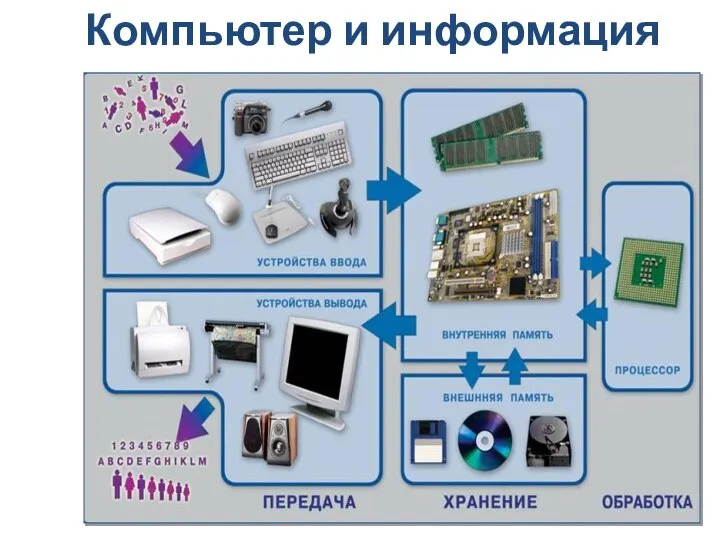 Компьютер и информация
Компьютер и информация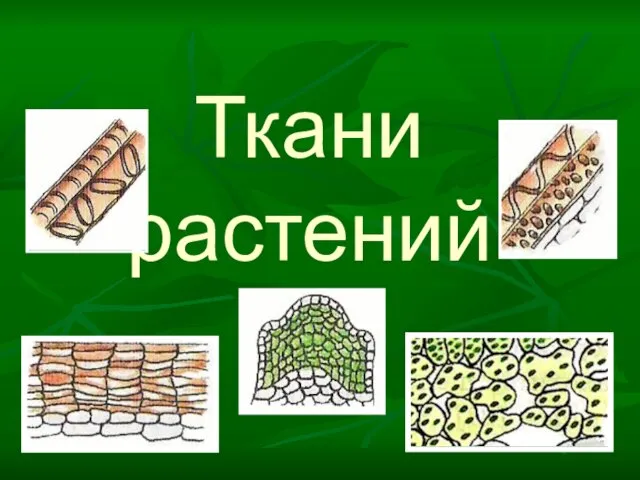 Ткани растений
Ткани растений Саратовская Государственная Консерватория
Саратовская Государственная Консерватория