Решение задачи с помощью составления системы уравнений с двумя переменными

Условие задачи(326)
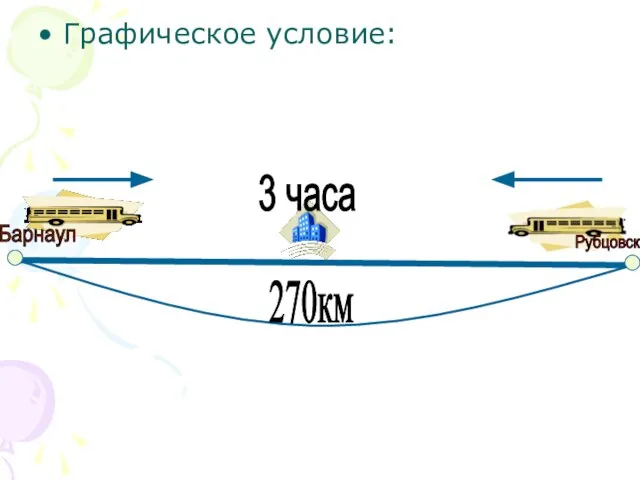
Из двух городов , расстояние между которыми 270 км, одновременно навстречу друг другу выехали два поезда и встретились через 3 часа. На весь путь один из поездов тратит на 1 ч 21 мин больше, чем другой. Найдите скорость обоих поездов.

Графическое условие:
Барнаул
Рубцовск
3 часа
270км

Решение :
Пусть X км/м – скорость первого поезда , а Y км/ч – скорость второго поезда.
Составим систему уравнений по условию задачи:
- т.к мы знаем весь путь и время, мы можем найти сумму скоростей, разделив путь на время, и получим первое уравнение: X+Y=90;

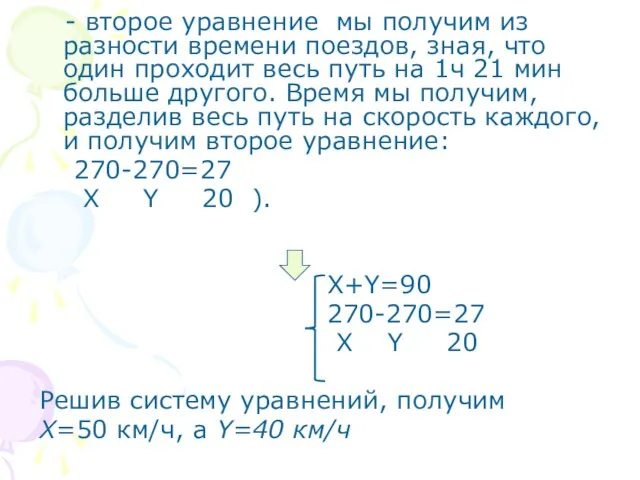
- второе уравнение мы получим из разности времени поездов, зная, что один проходит весь путь на 1ч 21 мин больше другого. Время мы получим, разделив весь путь на скорость каждого, и получим второе уравнение:
270-270=27
X Y 20 ).
X+Y=90
270-270=27
X Y 20
Решив систему уравнений, получим
X=50 км/ч, а Y=40 км/ч

Ответ:
50 км/ч, 40 км/ч.