Риск-анализ инвестиционных проектов на основе функций чувствительности и теории нечетких множеств

В.И.Котов
В.И.Котов
Содержание презентации
Проблемы анализа влияния рисков на финансовые результаты инвестиционных проектов (ИП)
Риски кредиторов
Подход к анализу рисков с точки зрения функций чувствительности
Нелинейные модели чувствительности
Теория нечетких множеств, как альтернатива вероятностному подходу
Расчет рисковой поправки в ставке дисконтирования

В.И.Котов
В.И.Котов
Основные определения:
Бизнес-процесс – последовательная смена состояний системы при взаимодействии ее с внешним окружением.
Владелец процесса – лицо, контролирующее бизнес-процесс и/или управляющее им, а также получающее выгоды (убытки) от протекания процесса в благоприятном (неблагоприятном) направлении.
Выгода (ущерб) – измеренное количественно или качественно позитивное (негативное) влияние, оказываемое со стороны процесса на своего владельца.
Благоприятное (неблагоприятное) развитие процесса – такое, в результате которого данный владелец процесса получает выгоду (ущерб).
Возможность – мера осуществимости, допустимости чего-либо. Областью значений возможности является единичный интервал [0,1]. Крайние точки: 0 – событие (ситуация) невозможна; 1 – событие (ситуация) неизбежна.
Риск – это возможность неблагоприятного развития процесса для данного владельца.
Шанс - это возможность благоприятного развития процесса для данного владельца.

Проблемы современного
риск-анализа
Результаты воздействия рисков всегда субъектно-ориентированы (инвесторы, кредиторы, менеджеры и персонал). Оценки рискованности и отношения к риску у всех субъектов различные.
В научной литературе широко представлены качественные методы риск-анализа.
Существующий инструментарий количественного риск-анализа весьма скудный и плохо приспособлен к практическим нуждам менеджеров и разработчиков проектов.
В известных количественных методах в ряде случаев не вполне адекватно используется теория вероятности.
В.И.Котов

В.И.Котов
В.И.Котов
В.И.Котов
Показатели риска кредиторов
Коэффициент текущей задолженности:
ОНСt – остаток непогашенных ссуд (долг к моменту t)
СОФt – стоимость основных фондов с учетом ликвидности
ЧПt – чистая прибыль
Аt – амортизационные отчисления
НСt – накопленные денежные средства к началу периода t

В.И.Котов
В.И.Котов
В.И.Котов
Требования к КТЗ(t)
Если данный коэффициент меньше единицы во всех периодах горизонта планирования, то это означает, что для кредитора отсутствует риск понести убытки в случае ее банкротства фирмы, реализующей ИП.
По европейским нормам этот показатель не должен превышать 0,75.
Таким образом кредитор страхует себя от риска банкротства фирмы, реализующей проект.

В.И.Котов
В.И.Котов
Снижение риска кредитора
Для снижения КТЗ(t) до приемлемой величины можно уменьшить объем заемных средств за счет увеличения собственных вложений.
При этом происходит перераспределение рисков: снижается риск кредитора и увеличивается риск собственников проекта.

В.И.Котов
В.И.Котов
В.И.Котов
Показатели риска кредиторов
(продолжение)
Коэффициент покрытия погашения ссуды и процентов
НСt – накопленные денежные средства к началу периода t
ЧПt – чистая прибыль после уплаты процентов по кредитам
Пt – проценты по кредиту
Аt – амортизационные отчисления
ПЗСt –полученные заемные средства в данном периоде
ВУКt – вложения в уставной капитал
Иt – инвестиции в данном периоде
ПСt – погашение ссуды (долга) в данном периоде

В.И.Котов
В.И.Котов
В.И.Котов
Требования к КППСиП(t)
В случае если КППСиП < 1, собственных средств для полного обслуживания задолженности не хватает и погашение взятых обязательств возможно лишь за счет привлечения в данном периоде новых кредитов или дополнительных вложений инвесторов.
При значениях 1 ≤ КППСиП ≤ 1.5 можно говорить о существовании зоны риска по выполнению кредитного соглашения.
Если значение данного показателя больше 1,5 – можно говорить о практическом отсутствии риска исполнения кредитного договора.

В.И.Котов
В.И.Котов
Снижение риска кредитора
Для увеличения КППСиП(t) в периоде t следует уменьшить долю погашения ссуды в этом периоде, отложив погашение на последующие периоды.
Это ведет к увеличению срока кредитования и росту процентных платежей.

В.И.Котов
В.И.Котов
В.И.Котов
Показатели риска кредиторов (продолжение)
Коэффициент покрытия погашения процентов
Заметим, что КППП ≥ КППСиП ∀ t. Если анализ КППСиП говорит об отсутствии риска, то необходимость анализировать КППП отпадает.
При наличии зоны риска по суммарным обязательствам, полезно знать, существует ли риск неуплаты процентов.
При значениях 1< КППП < 1.5 можно говорить о существовании зоны риска по выполнению кредитного соглашения.
В случае если значение данного показателя больше 1,5, можно говорить о практическом отсутствие риска не уплаты процентов.

В.И.Котов
В.И.Котов
При анализе влияния рисков
следует различать:
ИСТОЧНИКИ РИСКОВ
и
РИСКОВЫЕ СОБЫТИЯ
Источники рисков могут порождать или не порождать те или иные рисковые события, влияющие на проект.

В.И.Котов
В.И.Котов
Классификация источников риска
1. Внешние источники рисков (вне фирмы)
1.1. Политические (изменение внутренней и внешней политики государства, колебания международных отношений, таможенные пошлины, эмбарго, квоты на ввоз и вывоз капитала, ограничения на торговлю, международные санкции, смена правительства)
1.2. Юридические (изменения правовых норм в бизнесе, лицензирование, антимонопольное регулирование, нестабильность налогового законодательства, акцизы, штрафные санкции, правовая незащищенность бизнеса)
1.3. Макроэкономические (рост инфляции, колебания курсов иностранной валюты и валютное регулирование, колебание мировых цен на сырье, энергоносители, состояние фондового и финансового рынков, высокая ставка рефинансирования ЦБ РФ, спад или подъем экономики в стране)
1.4. Региональные (экономическое положение региона, степень развитости инфраструктуры, особенности географического положения, климат, регион-донор или дотационный)
1.5. Отраслевые (экономическое положение и инвестиционная привлекательность отрасли, фирма производит конечный продукт или полуфабрикат)
1.6. Рыночные (колебания платежеспособного спроса потребителей, влияние конкурентной среды, неустойчивость рынка поставщиков сырья, энергоресурсов, комплектующих, колебания процентных и депозитных ставок коммерческих банков, рост тарифов естественных монополий)
1.7. Форс-мажор (непредвиденные ситуации, стихийные бедствия, ЧП)

В.И.Котов
В.И.Котов
Классификация источников риска
(продолжение)
2. Внутренние источники рисков (внутри фирмы)
2.1. Организационные (неэффективность системы управления, недостаточный опыт и невысокое качество работы менеджеров)
2.2. Технологические (низкое качество технологических решений, недостатки в системе контроля технологических процессов и качества производимых товаров, физическая и моральная изношенность основных фондов)
2.3. Проектные (низкое качество проработки проекта, несогласованность проекта с внешней средой)
2.4. Маркетинговые (неадекватность оценки платежеспособного спроса, не гибкая ценовая политика, недооценка возможностей конкурентов)
2.5. Финансовые (недостаточность собственных финансовых ресурсов для инвестиций, ошибки в управлении финансами, недостаточность необходимых оборотных средств, неэффективное управление дебиторской и кредиторской задолженностью)
2.6. Юридические (ненадежность контрактов с поставщиками и потребителями, недостаточное правовое сопровождение бизнеса, действия менеджеров вне правового поля, арбитражные случаи)
2.7. Персональные (низкая квалификация и мотивация персонала, низкая приверженность персонала, низкая трудовая дисциплина)

Методы риск-анализа
Качественный метод – анализ источников риска с целью выявления актуальных рисковых событий. Определение риск-параметров динамической модели Cash-Flow соответствующих рисковым событиям. Оценка предельных отклонений риск-параметров.
Количественные методы – оценка границ отклонений целевых функций при воздействии совокупности рисков в пределах выбранного горизонта планирования. Интегральные оценки степени рискованности проекта. Принято различать:
Метод сценариев
Метод имитационного моделирования
Метод функций чувствительности
В.И.Котов

Методология риск-анализа
На этапе проектирования:
Качественный анализ источников риска для конкретного проекта
Прогнозный количественный риск-анализ проекта (оценка основных индикаторов риска).
Разработка мероприятий по снижению влияния рисков.
На этапе реализации проекта:
Мониторинг технологических, инвестиционных, коммерческих и финансовых результатов проекта в каждом периоде планирования.
Корректировка проекта на основе анализа расхождений прогноза и фактических результатов. Мониторинг динамики индикаторов риска.
В.И.Котов

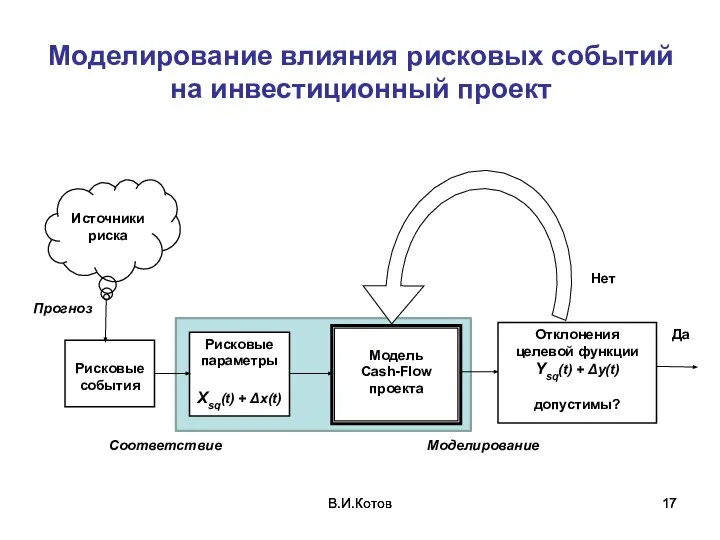
В.И.Котов
В.И.Котов
Моделирование влияния рисковых событий на инвестиционный проект

В.И.Котов
В.И.Котов
Варианты целевых функций:
ASCF(T) (Accumulated Saldo Cash-Flow) – накопленное сальдо денежных потоков (состояние расчетного счета проекта) к моменту Т
ANCF(T) (Accumulated Net Cash-Flow) – накопленный чистый денежный поток генерируемый проектом к моменту Т
NPV(T) (Net Present Value) – чистая текущая стоимость проекта к моменту Т
NCF(T) (Net Cash-Flow) – чистый денежный поток генерируемый проектом за период Т
PbP (PayBack Period) – срок окупаемости проекта
PI(T) (Profitability Index) – коэффициент внутренней экономической эффективности проекта к моменту Т
SCF(T) (Saldo Cash-Flow) – сальдо денежных потоков в момент (период) Т
IRR(T) (Internal Rate of Return) – внутренняя нома возврата (доходности) к моменту Т

В.И.Котов
ASCF(T) (Accumulated Saldo Cash-Flow – накопленное сальдо денежных потоков (состояние расчетного счета проекта) к моменту (периоду) Т
В.И.Котов

В.И.Котов
ANCF(T) (Accumulated Net Cash-Flow) – накопленный чистый денежный поток генерируемый проектом к моменту (периоду) Т
(без дисконтирования)
В.И.Котов

В.И.Котов
NPV(T) (Net Present Value) – чистая текущая стоимость проекта к моменту (периоду) Т
В.И.Котов

В.И.Котов
NCF(t) (Net Cash-Flow) – чистый денежный поток генерируемый проектом в момент (период) t
В.И.Котов

В.И.Котов
Срок окупаемости T= TbP
(Time back Period)
это решение трансцендентного уравнения:

В.И.Котов
Profitability Index – PIТ
Коэффициент внутренней экономической эффективности к моменту (периоду) Т

В.И.Котов
SCF(t) (Saldo Cash-Flow) – сальдо денежных потоков в момент (период) t
В.И.Котов

В.И.Котов
Внутренняя норма возврата IRR(T) к моменту (периоду) Т
– это решение нелинейного уравнения:

В.И.Котов
В.И.Котов
Определение функции чувствительности проекта к рискам
Целевая функция: Y(x,t)
Риск-параметры: xi (t)
Относительная функция чувствительности (при бесконечно малых отклонениях):

В.И.Котов
Экономический смысл
Чувствительность показывает на сколько процентов изменится целевая функция при изменении риск-параметра на один процент.

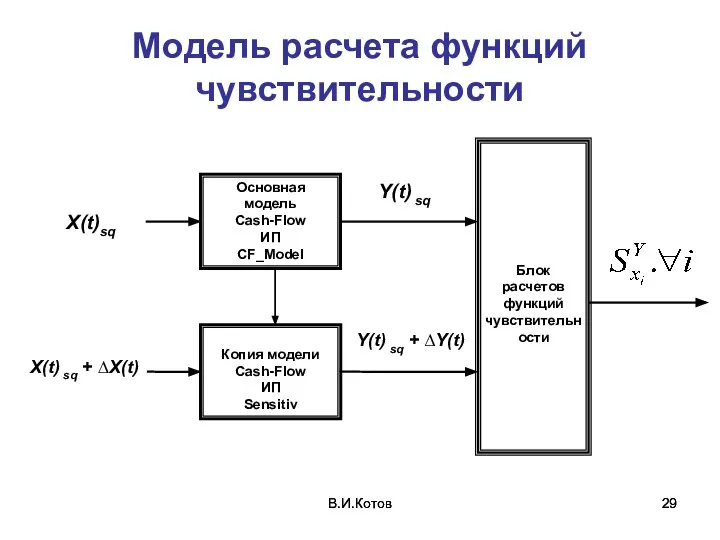
В.И.Котов
В.И.Котов
Модель расчета функций чувствительности

Работа с моделью
Два файла модели связаны друг с другом.
Файлы не переименовывать. Имя папки это фамилия студента и номер группы.
Копировать можно только всю папку с файлами.
В файлах модели не вставлять и не удалять строки, столбцы или ячейки.
Не пользоваться «ножницами» (вырезать).
В листе MainModel файла Sensitiv в клетках AD20-AD24 должны быть нули (это проверка синхронности модели).
При работе открывать оба файла и закрывать с сохранением.
Защиту листов не снимать. Желтые клетки для ввода исходных данных.
В.И.Котов

В.И.Котов
В.И.Котов
Свойства функций чувствительности
(для всех целевых функций, кроме NPV)
S(t) ≥ 0 для всех t по всем ценам и натуральным объемам продаж товаров, реализуемых в рамках инвестиционного проекта (исключая товары с отрицательной рентабельностью)
S(t) ≤ 0 для всех t по всем статьям текущих расходов, а также по ставке процента коммерческих кредитов

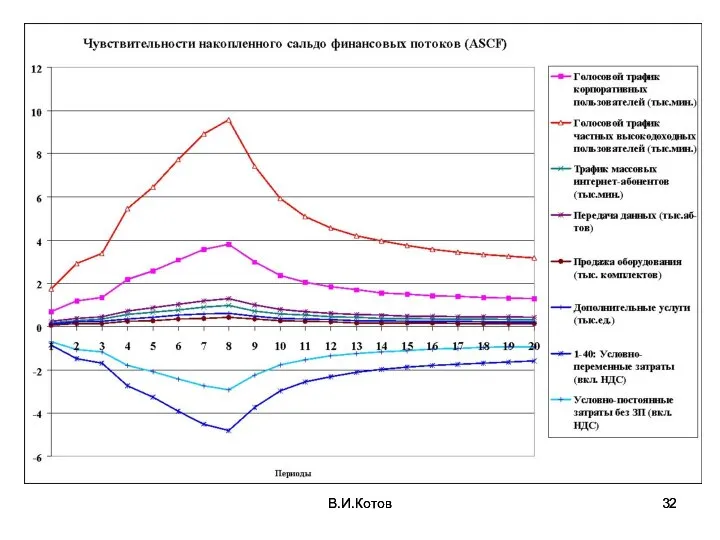
В.И.Котов
В.И.Котов

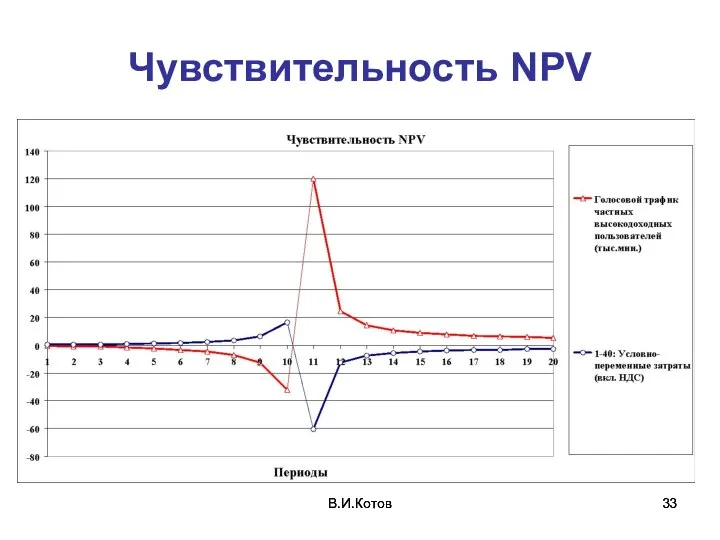
В.И.Котов
В.И.Котов
Чувствительность NPV

В.И.Котов
В.И.Котов
Что дает знание функций чувствительности?
Позволяет ранжировать риски, выделяя наиболее существенные.
Позволяет определить наиболее «опасный» период жизни проекта.
Позволяет количественно сравнивать степени рискованности сценариев или различных проектов между собой.
Позволяет оценить влияние на проект совокупности рисков.

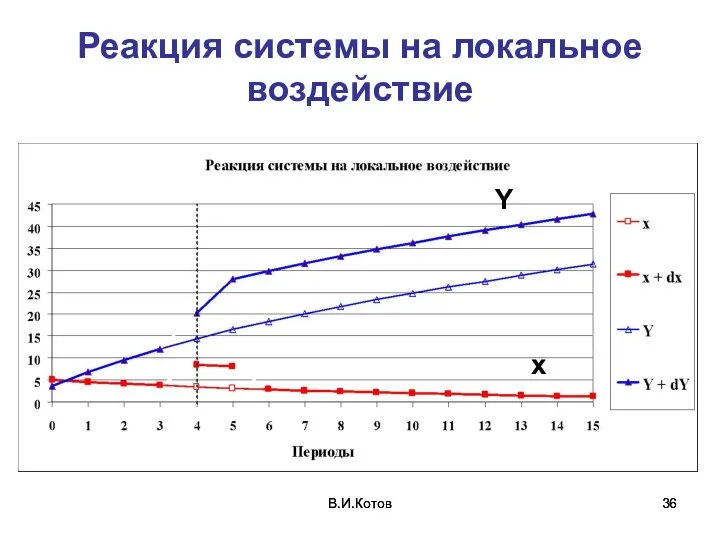
В.И.Котов
В.И.Котов
Локальная чувствительность (LS)
(определение)
– чувствительность при локальном (краткосрочном во времени) воздействии риск-параметра, т.е. когда его отклонение имеет место только в течение одного или нескольких периодов, существенно меньших общего горизонта планирования

В.И.Котов
В.И.Котов
Реакция системы на локальное воздействие
Y
x

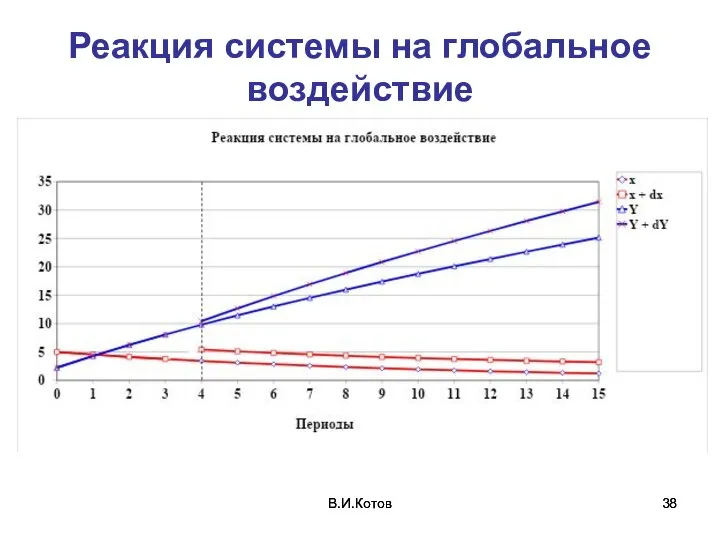
В.И.Котов
В.И.Котов
Глобальная чувствительность (GS)
(определение)
– чувствительность при глобальном (длительном по времени) воздействии риск-параметра, т.е. когда его отклонение, начиная с некоторого момента, может длиться вплоть до конца горизонта планирования

В.И.Котов
В.И.Котов
Реакция системы на глобальное воздействие

В.И.Котов
В.И.Котов
В.И.Котов
Что дает знание функций чувствительности?
Позволяет ранжировать риски, выделяя наиболее существенные.
Позволяет определить наиболее «опасный» (высокая чувствительность) период жизни проекта в пределах горизонта планирования.
Позволяет количественно сравнивать степени рискованности сценариев или различных проектов между собой.
Позволяет оценить одновременное влияние на проект совокупности рисков и оценить границы отклонения целевой функции в пределах всего горизонта планирования.

В.И.Котов
В.И.Котов
Рисковые характеристики сценария реализации проекта
Функции чувствительности вместе с показателями эффективности являются важными характеристиками проекта.
Знание этих характеристик существенно расширяет представление о реализуемости проекта в условиях риска.
Принимая решение о выборе того или иного возможного варианта (сценария) финансового прогноза, при прочих равных условиях следует отдавать предпочтение варианту с наименьшей чувствительностью.
Как же сравнивать сценарии и различные проекты между собой по степени их рискованности?

В.И.Котов
В.И.Котов
Влияние совокупности рисков
Если определены чувствительности независимо по всем N риск-параметрам, то можно выразить полное относительное отклонение целевой функции через реальные относительные отклонения аргументов в следующем виде:

В.И.Котов
В.И.Котов
Минимизация чувствительности
при выборе сценария
Выбираем тот вариант сценария, у которого:
Для большей информативности можно разбить все риск-параметры на следующие группы:
Натуральные объемы продаж
Статьи текущих затрат (условно-постоянные и условно-переменные)
Инвестиционные затраты

Интегральные индексы чувствительности инвестиционного проекта
В.И.Котов

В.И.Котов
В.И.Котов
Индекс максимальной чувствительности к объемам продаж
Xq – вектор натуральных объемов продаж по всем позициям ассортимента из М товаров
M – количество реализуемых товаров в ассортименте

В.И.Котов
В.И.Котов
Индекс максимальной чувствительности к текущим издержкам
Xc – вектор из L статей текущих издержек

В.И.Котов
В.И.Котов
Индекс максимальной чувствительности к инвестиционным затратам
XIn – вектор из K статей инвестиционных затрат

В.И.Котов
Экономический смысл IMS
Индекс максимальной чувствительности показывает на сколько процентов максимально может измениться целевая функция в пределах горизонта планирования, если одновременно все риск-параметры изменятся на один процент в неблагоприятном направлении.

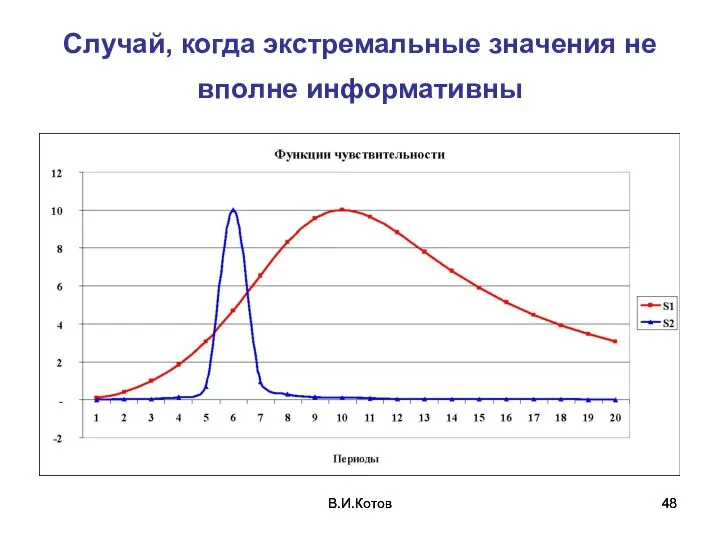
В.И.Котов
В.И.Котов
Случай, когда экстремальные значения не вполне информативны

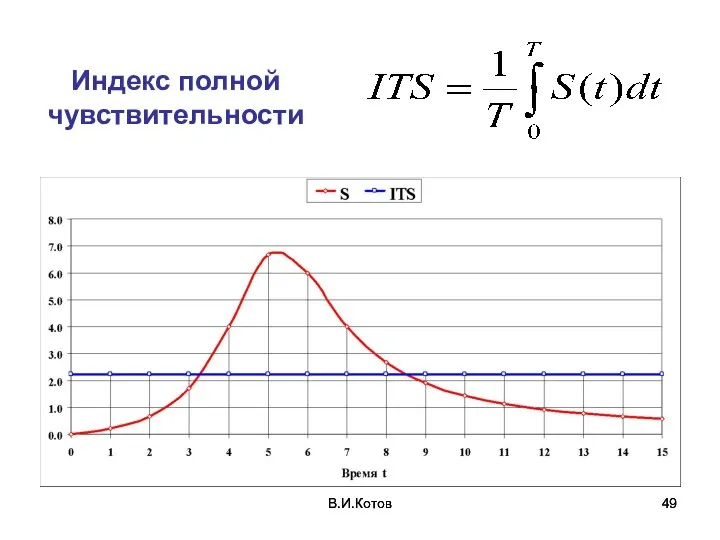
В.И.Котов
В.И.Котов
Индекс полной чувствительности

Индекс полной чувствительности к натуральным объемам продаж
при трапецеидальной аппроксимации
В.И.Котов

Индекс полной чувствительности к текущим издержкам
при трапецеидальной аппроксимации
В.И.Котов

Индекс полной чувствительности к инвестиционным затратам
при трапецеидальной аппроксимации
В.И.Котов

В.И.Котов
Экономический смысл ITS
Индекс полной чувствительности показывает на сколько процентов
в среднем может измениться целевая функция в пределах горизонта планирования, если одновременно все риск-параметры изменятся на один процент в неблагоприятном направлении.

В.И.Котов
В.И.Котов
При сравнении проектов по степени рискованности
Рассчитываются функции чувствительности для всех инвестиционных проектов (ИП)
Рассчитываются индексы максимальной и полной чувствительности для всех ИП
Проводится сравнительный анализ проектов по полученным индексам

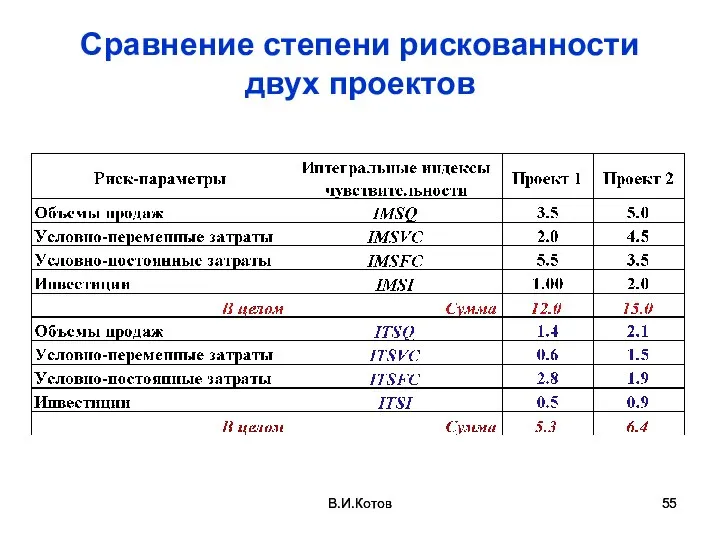
В.И.Котов
Сравнение степени рискованности двух проектов
В.И.Котов

НЕЛИНЕЙНАЯ МОДЕЛЬ
ЧУВСТВИТЕЛЬНОСТИ
В.И.Котов

В.И.Котов
Общее определение линейности системы
Система (в том числе экономическая) линейна, если выполняются условия аддитивности и гомогенности.
Необходимо проверить выполнение этих условий для выбранной целевой функции по всем риск-параметрам.

В.И.Котов
Условие аддитивности
Целевая функция аддитивна, если реакция экономической системы на совокупность воздействий (рисков) равна сумме ее реакций на каждое воздействие (риск) в отдельности.
Это известный принцип суперпозиции, который можно выразить в следующей форме:
В.И.Котов

В.И.Котов
Условие гомогенности
Строго говоря, необходимо проверить выполнение для системы условия гомогенности (пропорциональности)
Если риск-параметр увеличить в а раз, то целевая функция увеличится во столько же раз:
Y(ax) = a Y(x),
где а – некоторая произвольная константа,
x – вектор риск-параметров .

В.И.Котов
Для линейности экономической системы достаточно выполнения условия аддитивности
Это означает, что
выполнение условия аддитивности (принципа суперпозиции) практически гарантирует линейность экономической системы.

В.И.Котов
Нелинейная модель чувствительности
До сих пор мы полагали, что целевая функция (ЦФ) линейно зависит от каждого риск-параметра.
Для ЦФ, измеряемых в денежных единицах в большинстве случаев это верно.
В начальной стадии реализации ИП возможно нарушение линейности, например из-за перехода от убытков к прибыли (ЦФ становится кусочно-гладкой).
Возможна взаимная зависимость отдельных риск-параметров (например: объем продаж и условно-переменные затраты).
В этих случаях нужна нелинейная модель второго порядка.

В.И.Котов
Ряд Тейлора для абсолютного отклонения целевой функции
(линейная и квадратичная составляющие):

В.И.Котов
Общая нелинейная модель чувствительности второго порядка

В.И.Котов
Нелинейная модель чувствительности для одного риск-параметра

В.И.Котов
Метод двух экспериментов для определения чувствительностей
(первый вариант)

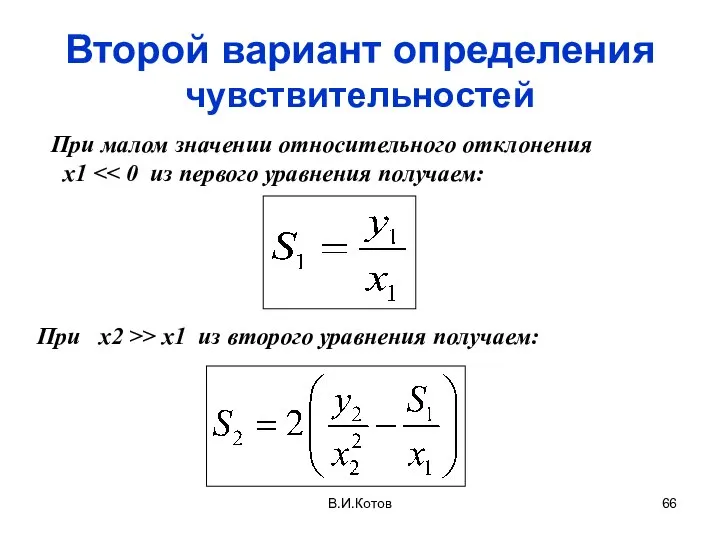
В.И.Котов
Второй вариант определения чувствительностей

В.И.Котов
Нелинейная модель чувствительности для двух риск-параметров

Экономический смысл взаимной чувствительности
Взаимная чувствительность показывает на сколько процентов полное относительное отклонение целевой функции отличается от суммы линейного и нелинейного относительных отклонений при одновременном изменении двух риск-параметров на один процент в неблагоприятном направлении.
В.И.Котов

Если цена Р и натуральный объем продаж Q являются риск-параметрами, то Y(p,Q)
В этом случае можно в качестве риск-параметра выбрать выручку B = pQ, тогда модель линейна.
В случае, когда p и Q независимые риск-параметры, тогда модель не линейна, т.к. целевая функция зависит от произведения этих параметров. Для оценки влияния совокупности рисков используем формулу:
Здесь в N вошли p и Q, а их взаимная чувствительность SpQ равна единице.
В.И.Котов

В.И.Котов
Метод функций чувствительности является универсальным инструментом риск-анализа и свободен от приписываемых ему недостатков
«Недостатки»:
1. Метод чувствительности является «однофакторным».
Если рассчитаны чувствительности по каждому риску в отдельности, то влияние любой совокупности рисков легко рассчитывается на основе предложенной модели.
2. Метод не работает, когда риски зависят друг от друга.
Нелинейная модель чувствительности позволяет учесть не только взаимное влияние рисков, но и нелинейность модели инвестиционного проекта.

В.И.Котов
В.И.Котов
Неопределенность
Неопределенность – это неустранимое свойство рыночной среды, связанное с тем, что на рынке одновременно действует множество факторов различной природы и направленности, корректная совокупная оценка которых практически невозможна.
Рыночная неопределенность не обладает статистической природой, т.к. окружающая фирму бизнес-среда постоянно меняется под воздействием различных факторов, включая человеческий фактор.
«Проклятье» экономических систем:
«Нельзя дважды войти в одну и ту же реку».

В.И.Котов
В.И.Котов
Вероятность и возможность
При анализе процессов, подчиняющихся статистическим законам, можно использовать теорию вероятности.
Для бизнес процессов и систем с интеллектом, т.е. там где люди принимают решения, не существует надежной статистики. Невозможно обеспечить однородность и одинаковость условий эксперимента для расчета вероятности по статистически значимой выборке. Классическая теория вероятности здесь не работает.
При анализе таких систем необходимо использовать теорию возможностей , в основе которой лежит теория нечетких множеств.

В.И.Котов
В.И.Котов
Нечеткие множества
(этапы развития теории)
В 1965 году Лотфи А. Заде (Lotfi A. Zadeh), профессор информатики университета в Беркли (Калифорния), ввел в науку понятие нечетких множеств (fuzzy sets или fuzzy logic), давшее название одноименной теории.
В 1971 году Л.Заде выступил с докладом по ТНМ в СССР, в Москве на международном математическом конгрессе.
С 1975 года начался бурный рост прикладных работ в различных отраслях.
Интеграция ТНМ с классической теорией вероятности привела к появлению теории возможности (эвентология).

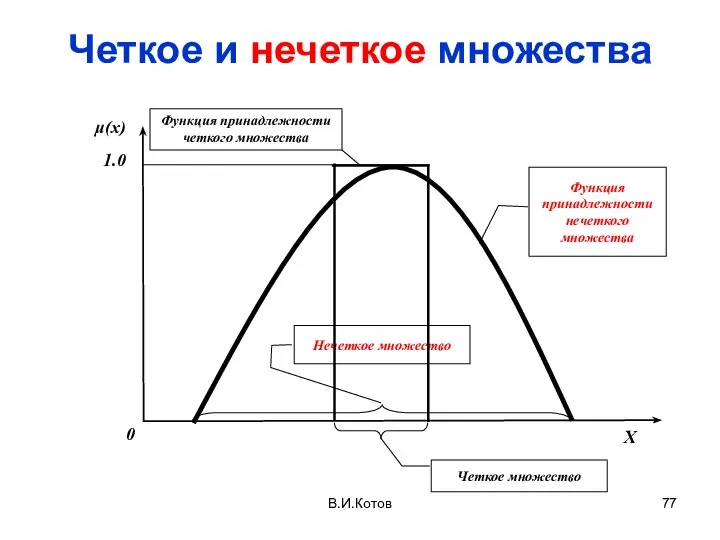
В.И.Котов
Четкие и нечеткие множества
Для ЧМ элемент либо принадлежит этому множеству, либо нет – третьего не дано (Закон исключённого третьего).
Для НМ элемент может не вполне принадлежать этому множеству.
Степень принадлежности определяется соответствующей функцией принадлежности 0 ≤ µ(x) ≤ 1
В.И.Котов

В.И.Котов
В.И.Котов
Основные определения
Носитель U – это универсальное множество, к которому относятся все результаты наблюдений x в рамках оцениваемой квазистатистики.
Нечеткое множество – это множество значений носителя, такое, что каждому значению носителя x ∈ U сопоставлена степень принадлежности 0 ≤ μА(x) ≤ 1 этого значения множеству А.

В.И.Котов
В.И.Котов
Основные определения
(продолжение)
Функция принадлежности μА(x) – это функция, областью определения которой является носитель U, x ∈ U, а областью значений – единичный интервал [0,1].
Чем больше μА(x), тем выше оценивается степень принадлежности элемента носителя x нечеткому множеству А.

В.И.Котов
Четкое и нечеткое множества
Функция принадлежности четкого множества

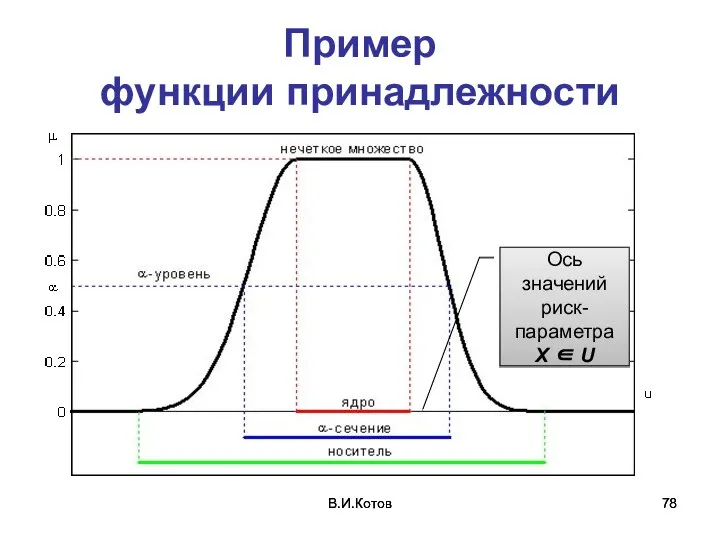
В.И.Котов
В.И.Котов
Пример
функции принадлежности
Ось значений риск-параметра X ∈ U

В.И.Котов
Нечеткие числа и операции
над ними
Нечеткое число – это нечеткое подмножество множества действительных чисел (носителя), имеющее нормальную и выпуклую функцию принадлежности, то есть такую, что:
а) существует значение носителя, в котором функция принадлежности равна единице (условие нормальности),
б) при отступлении от своего максимума влево или вправо функция принадлежности убывает (условие выпуклости).

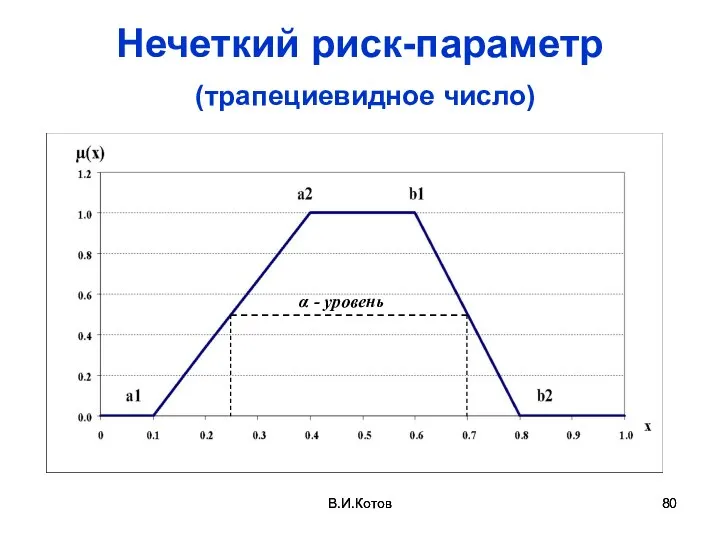
В.И.Котов
В.И.Котов
Нечеткий риск-параметр
(трапециевидное число)
α - уровень

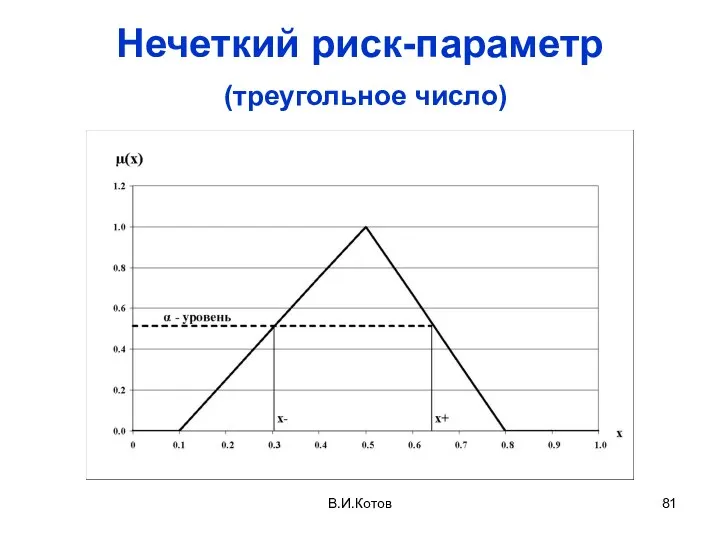
В.И.Котов
Нечеткий риск-параметр
(треугольное число)

В.И.Котов
Свойства треугольных и трапециевидных чисел
действительное число есть частный случай треугольного нечеткого числа;
сумма треугольных чисел есть треугольное число;
треугольное (трапециевидное) число, умноженное на действительное число, есть треугольное (трапециевидное) число;
сумма трапециевидных чисел есть трапециевидное число;
сумма треугольного и трапециевидного чисел есть трапециевидное число.

В.И.Котов
В.И.Котов
Мягкие вычисления
(нечеткая арифметика)
Для любого α-уровня принадлежности:
операция "сложения":
[a1, a2] (+) [b1, b2] = [a1 + b1, a2 + b2],
операция "вычитания":
[a1, a2] (-) [b1, b2] = [a1 - b2, a2 - b1],
операция "умножения":
[a1, a2] (×) [b1, b2] = [a1 × b1, a2 × b2],
операция "деления":
[a1, a2] (/) [b1, b2] = [a1 / b2, a2 / b1],
операция "возведения в степень":
[a1, a2] (^) i = [a1i , a2i].

В.И.Котов
Нечеткие функции
Поле нечетких чисел – это несчетное множество нечетких чисел.
Нечеткая функция – это взаимно однозначное соответствие двух полей нечетких чисел: аргумента и функции.
Вид нечеткой функции определяется видом чисел области ее определения (треугольные, трапециевидные и др.)

В.И.Котов
Свойства нечетких функций
сложение: сумма (разность) треугольных функций есть треугольная функция;
умножение на число переводит треугольную функцию в треугольную функцию;
дифференцирование (интегрирование) треугольной нечеткой функции проводится по правилам вещественного дифференцирования (интегрирования):

В.И.Котов
В.И.Котов
α-уровневый принцип обобщения
Пусть:
- функция от n независимых переменных с аргументами xi
заданными нечеткими числами:
где x± - верхняя и нижняя абсцисса α–уровня.

В.И.Котов
В.И.Котов
α-уровневый принцип обобщения
(продолжение)
Значением нечеткой функции:
называется нечеткое число:

В.И.Котов
В.И.Котов
α-уровневый принцип обобщения
(продолжение)
Нижняя (-) и верхняя (+) границы α–уровня нечеткой функции будут, соответственно:

В.И.Котов
В.И.Котов
α-уровневый принцип обобщения
(окончание)
Применение α-уровневого принципа обобщения сводится к решению для каждого α–уровня следующей задачи оптимизации:
Найти минимальное и максимальное значения функции:
при условии, что аргументы могут принимать значения из соответствующих α–уровневых множеств.

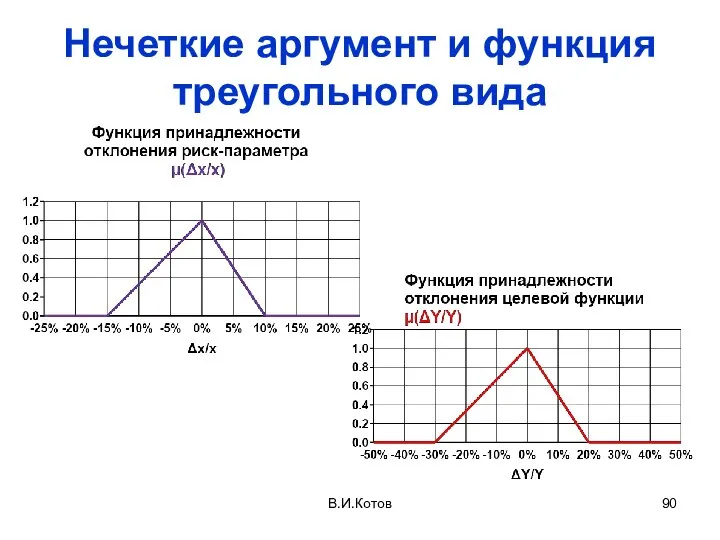
Нечеткие аргумент и функция треугольного вида
В.И.Котов

В.И.Котов
Функция: «Прогноз продаж за период t» есть треугольное число [F2(t), F3(t), F1(t)]

В.И.Котов
В.И.Котов
Оценка одновременного влияния совокупности рисков
Полное относительное отклонение целевой
функции при воздействии N рисков:
На этапе качественного риск-анализа, для каждого из N нечетких относительных отклонений риск-параметров хi определим максимальные границы интервалов достоверности (треугольные числа):

В.И.Котов
В.И.Котов
Нечеткое относительное отклонение целевой функции (ЦФ) треугольного типа
На основе «мягких» вычислений находим границы интервалов достоверности, которые определяют треугольное число относительного отклонения ЦФ:

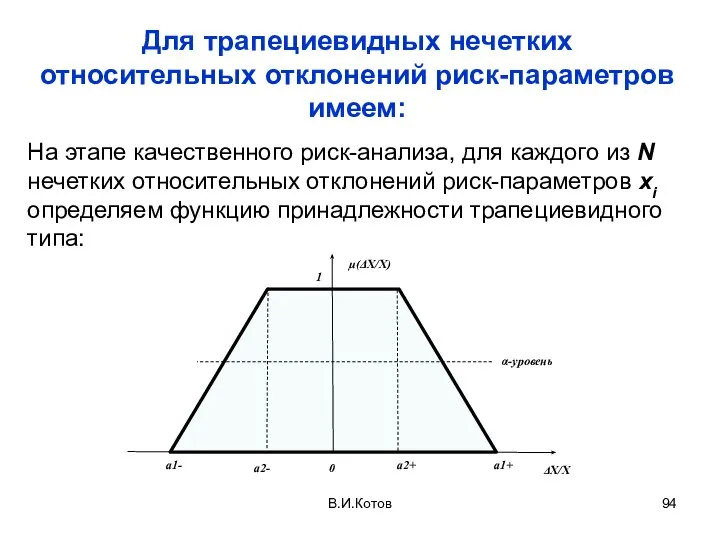
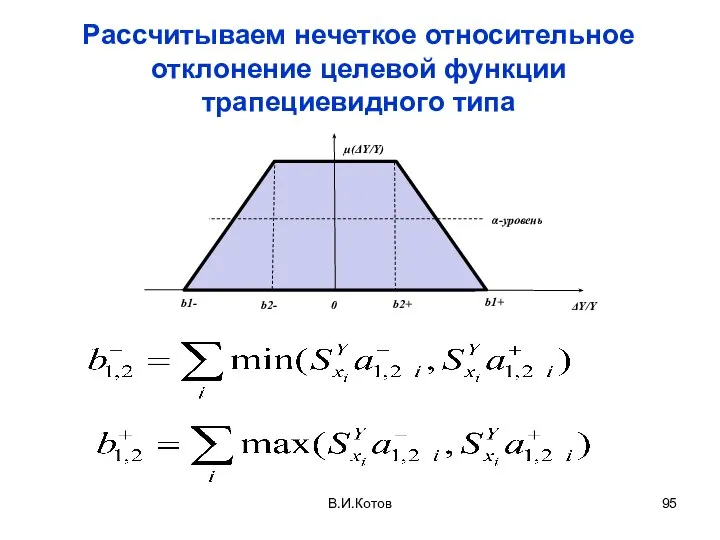
Для трапециевидных нечетких относительных отклонений риск-параметров имеем:
На этапе качественного риск-анализа, для каждого из N нечетких относительных отклонений риск-параметров хi определяем функцию принадлежности трапециевидного типа:
В.И.Котов

Рассчитываем нечеткое относительное отклонение целевой функции трапециевидного типа
В.И.Котов

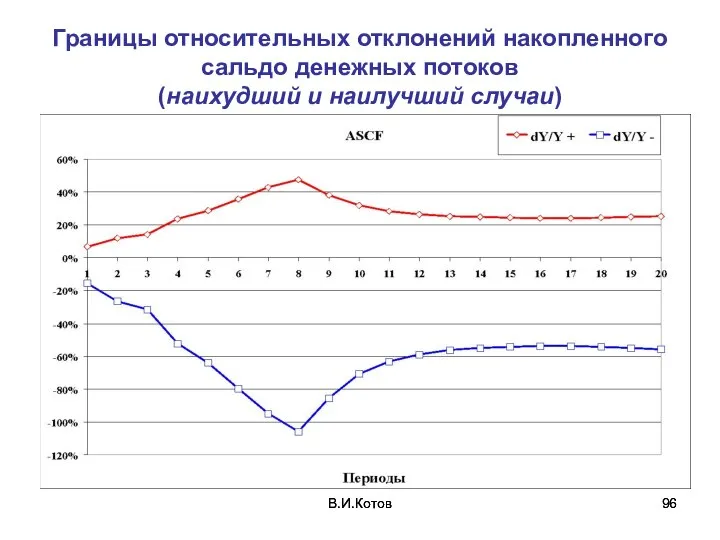
В.И.Котов
В.И.Котов
Границы относительных отклонений накопленного сальдо денежных потоков
(наихудший и наилучший случаи)

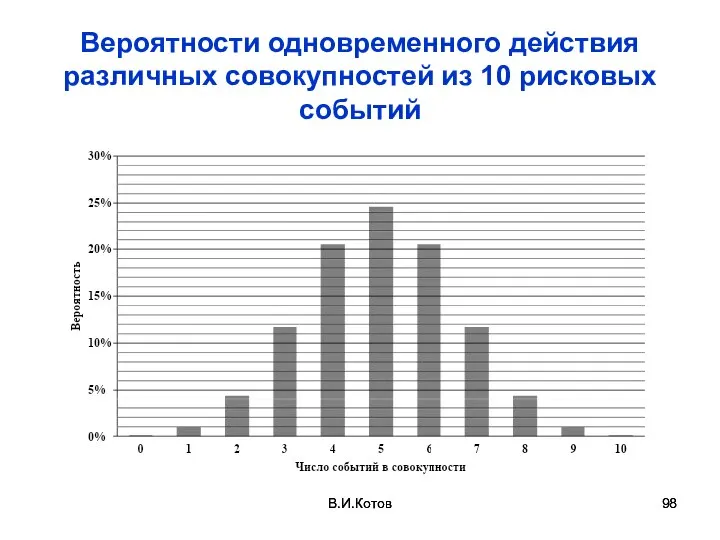
В.И.Котов
В.И.Котов
Оценка вероятности одновременного воздействия k рисковых событий из N
Число комбинаций из N событий по k:
Вероятность появления случайной совокупности, состоящей из k событий, будет:
В.И.Котов

В.И.Котов
Вероятности одновременного действия различных совокупностей из 10 рисковых событий
В.И.Котов

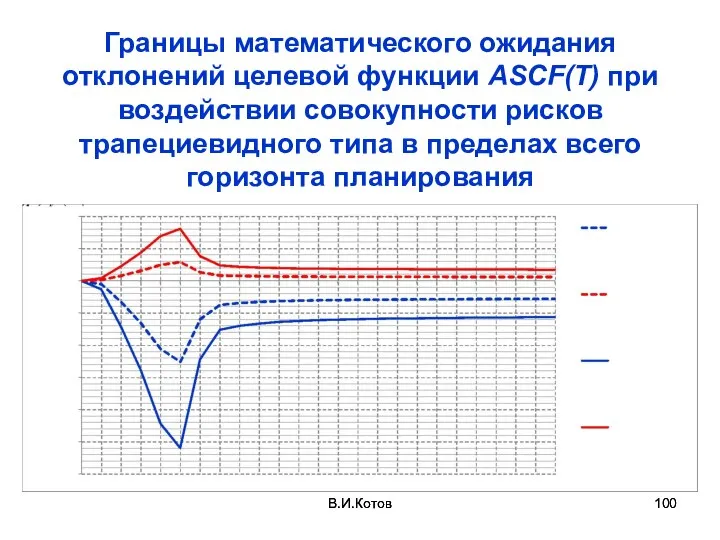
Нечеткая оценка математического ожидания границ отклонения целевой функции при одновременном воздействии совокупности рисков
Теорема: при воздействии на экономическую систему (фирма, инвестиционный проект и др.) одновременно любой случайной k-совокупности из множества независимых N рисковых событий, математическое ожидание относительного отклонения целевой функции системы (с учетом ее чувствительности к этим рискам) будет вдвое меньше, чем в предположении, что все N рисков будут действовать одновременно (наихудший случай).
В.И.Котов

В.И.Котов
Границы математического ожидания отклонений целевой функции ASCF(T) при воздействии совокупности рисков трапециевидного типа в пределах всего горизонта планирования
В.И.Котов

Математическое ожидание функции принадлежности µ(х)
Поскольку мы не знаем вероятности попадания нечеткого риск-параметра в любой интервал, связанный с α -уровнем функции принадлежности, используем принцип Лапласа: «если вероятности различных состояний экономической системы неизвестны, то следует считать эти состояния равновероятными». Тогда:
откуда следует:
при - случай треугольного нечеткого числа.
при - случай прямоугольного нечеткого числа.
для любого трапециевидного нечеткого числа
В.И.Котов

В.И.Котов
Нечеткая модель риск-анализа на основе функций чувствительности позволяет:
В четыре раза (при риск-параметрах треугольного типа) сократить зону неопределенности для целевой функции при воздействии различных совокупностей рисков по всему горизонту планирования по сравнению с методом сценариев (пессимистический и оптимистический варианты).
Рассчитать рисковую поправку в ставке дисконтирования для любого инвестиционного проекта на основе чувствительности NPV(T).

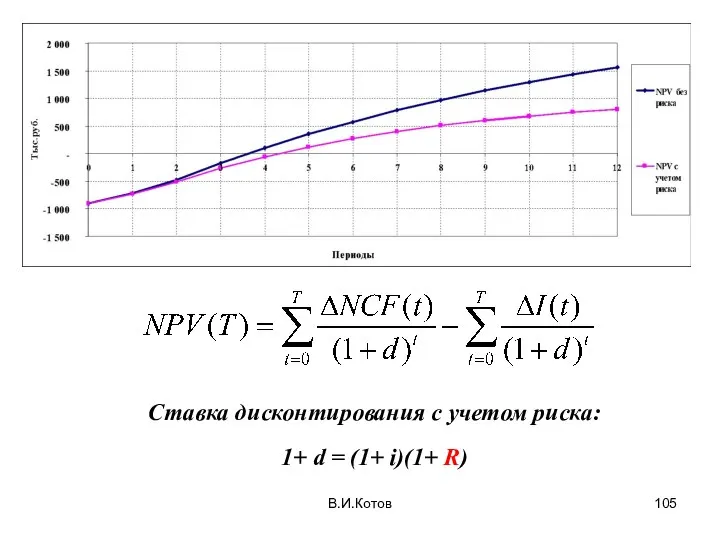
В.И.Котов
В.И.Котов
Оценка рисковой составляющей в ставке дисконта
Ставка дисконта: 1 + d = ( 1 + i )( 1 + R )
Вычисляем NPVбр(T) при безрисковой ставке дисконта: 1 + d0 = ( 1 + i ).
Для выбранных возможных отклонений риск-параметров с помощью нечеткой модели находим относительное уменьшение δNPVбр(T)=h < 0 при воздействии совокупности рисков.
Вычисляем в конце горизонта планирования предельное значение NPV(T) с учетом всех рисков:
NPVпред(T) = NPVбр(T) [1+ h]

В.И.Котов
В.И.Котов
Оценка рисковой составляющей в ставке дисконта (продолжение)
Возвращаемся к исходной модели и с помощью опции «Подбор параметра» в EXCEL находим то значение ставки дисконта d, при которой NPV(T) = NPVпред(T). Эта ставка d будет искомой ставкой дисконта с учетом всех рисков.
Далее вычисляем рисковую составляющую 1+R ставки дисконта, а именно:
R = (1+ d ) / (1+ d0 ) - 1 = (1 + d ) / (1 + i ) - 1

В.И.Котов

Расчет рисковой поправки
(пример)
В.И.Котов
Ставка дисконтирования без учета риска:
1 + d0 = 1 + i = 1.1 при i = 10% ,
тогда NPV(T=12) = 1561
При воздействии совокупности рисков:
NPV(T=12) = 900,
что соответствует ставке дисконта
d = 16.39,
откуда получаем:
R = ( 1 + d ) / (1 + d0 ) – 1 = 5.81%