с анимацией

Производная - задания В8
Готовимся к ЕГЭ
* по графику функции
* по графику производной
→
о производной
и касательной
→
о свойствах функции
и касательной
В8. Тематика задач:
* значение производной в точке
по графику функции
и касательной
тангенс угла наклона касательной к графику функции в точке Хо.
* у = k х + в - касательная
→
f’ (x₀) = k.
Как найти
наибольшее
наименьшее
значение функции
на отрезке [a;b]
точку
максимума
минимума
функции
экстремум
2
→

Функция убывает.
•
-7
°
8
у = 0
у = 0
у = 0
3. Нули функции – пересечения графика с ОХ, у = 0.
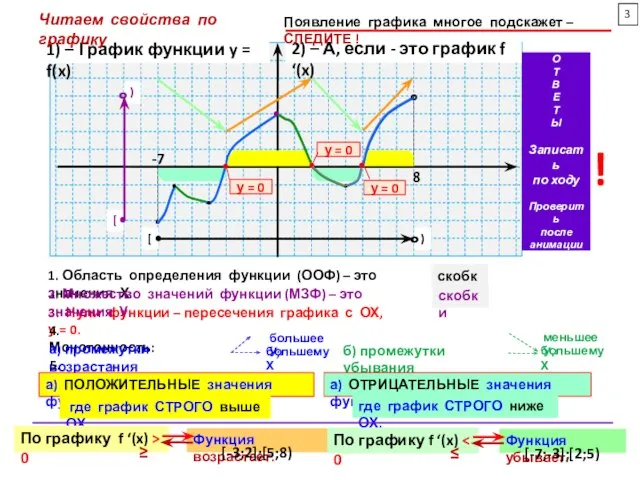
1) – График функции y = f(x)
1. Область определения функции (ООФ) – это значения Х.
[
)
2. Множество значений функции (МЗФ) – это значения У.
скобки
скобки
[
)
4. Монотонность:
а) промежутки возрастания
б) промежутки убывания
большему Х
большее У;
большему Х
меньшее У.
5. Знакопостоянство:
а) ПОЛОЖИТЕЛЬНЫЕ значения функции,
где график СТРОГО выше ОХ.
а) ОТРИЦАТЕЛЬНЫЕ значения функции,
•
•
•
•
•
•
где график СТРОГО ниже ОХ.
Читаем свойства по графику
2) – А, если - это график f ‘(x)
По графику f ‘(x) > 0
Функция возрастает.
По графику f ‘(x) < 0
1. [-7;8).
2. [-3;4).
3. -3;2;5.
4a. [-7;-6];
[-4;0];[4;8).
4в. [-6;-4];
[0;4].
5a. (-3;2)u
(5;8).
5в. [-7;-3)u
(2;5).
•
[-7;-3];[2;5)
О
Т
В
Е
Т
Ы
Записать
по ходу
Проверить
после
анимации
Появление графика многое подскажет – СЛЕДИТЕ !
3
•
°
•
°
≥
≤
[-3;2];[5;8)
!

Влияния знака производной на изменения функции
Свойства функции по графику её ПРОИЗВОДНОЙ
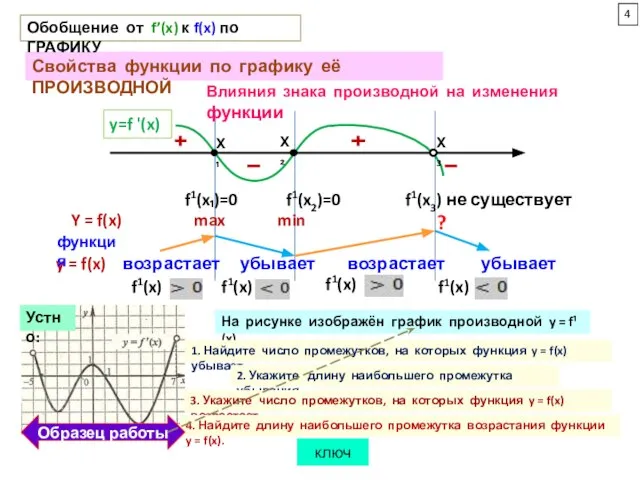
f1(x₁)=0 f1(x2)=0 f1(x3) не существует
y = f(x) возрастает убывает возрастает убывает
f1(x)
f1(x)
f1(x)
Х₁
Х₂
Х₃
f1(x)
?
y=f '(x)
На рисунке изображён график производной y = f¹(x).
1. Найдите число промежутков, на которых функция y = f(x) убывает.
2. Укажите длину наибольшего промежутка убывания.
3. Укажите число промежутков, на которых функция y = f(x) возрастает.
4. Найдите длину наибольшего промежутка возрастания функции y = f(x).
функция
Устно:
4
2; 5; 3; 2
ключ
Y = f(x) max min
Образец работы
Обобщение от f’(x) к f(x) по ГРАФИКУ

План действий с каждой задачей
Левой клавишей мыши: «Показ слайдов», «С текущего слайда»
1.Решайте сначала задание самостоятельно !
2. Левой клавишей мыши
* кликнуть ОТВЕТ.
3. Левой клавишей мыши
* кликнуть ПРОСМОТР РЕШЕНИЯ:
- на что опираемся в поиске ответа,
- анимация решения на рисунке
4. Левой клавишей мыши
* УБИРАЕТСЯ РЕШЕНИЕ
* кликнуть следующую задачу.
(в заключение ещё раз читайте задачу и пояснение)
5

Целые точки
f’(x) < 0 - промежутки,
на которых f(x) убывает !
2 + 5
большему Х
меньшее У.
решение
Целые точки
На рисунке изображен график функции y = f(x), определенной на интервале (-5;8).
В 8. Повторяем. Учимся. Закрепляем. Тренируемся.
y = f(x)
y= k x + b – касательные,
f’(x) = 0 в точках максимума и минимума !
2. Определите количество
целых точек, в которых
производная функции f(x)
положительна.
3
f’(x) > 0 там,
где f(x) возрастает !
•
•
•
•
7
•
•
•
•
2
5
№№ 1-3
6
1
0
8
- 5
ı
ı
ο
ο
•
•
•
•
•
большему Х
большее У;
т. е. k = 0, f’(x) = 0 !!!
сравнив, у = 0∙х - 16
По графику функции
параллельны ОХ
←
8
2. Определите количество
целых точек, в которых
решение
решение

Найдите количество точек, в которых производная
функции y=f(x) равна 0.
7
5. На рисунке изображен график функции y=f(x),
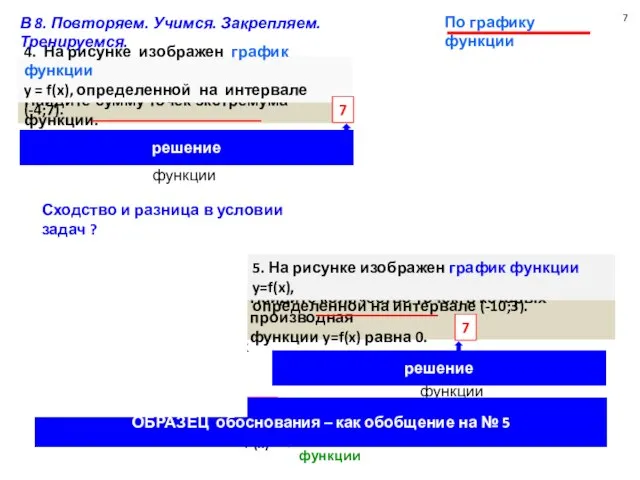
определённой на интервале (-10;3).
Производная f’(x) = 0
вершины графика функции
Сколько точек ?
решение
Найдите сумму точек экстремума функции.
•
•
•
•
•
•
-3
-2
1
2
3
6
№ 4
Точки экстремума
4. На рисунке изображен график функции
y = f(x), определенной на интервале (-4;7).
y = f(x)
- 4
ı
7
1
0
В 8. Повторяем. Учимся. Закрепляем. Тренируемся.
По графику функции
7
- 3
- 2
+ 1
+ 2
+ 3
+ 6
вершины графика функции
f’= 0
решение
7
-10
0
3
1
х
у
y=f(x)
°
°
¯
'
'
Сходство и разница в условии задач ?
Монотонность функции по графику
Знак
f’(x)
-
-
-
-
+
+
+
+
Знак f’(x) меняется в вершинах графика функции
ОБРАЗЕЦ обоснования – как обобщение на № 5
•
•
•
•
•
•
•

На рисунке изображен график производной функции f(x), определенной на интервале (-1;21).
Найдите количество точек экстремума
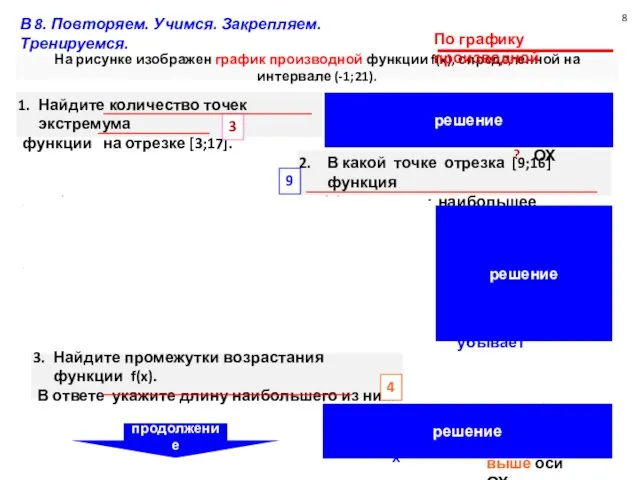
функции на отрезке [3;17].
Найдите промежутки возрастания функции f(x).
В ответе укажите длину наибольшего из них.
ο
В какой точке отрезка [9;16] функция
y=f(x) принимает наибольшее значение?
'
y = f’(x), №№ 1 - 3
21
-1
ο
'
¯
1
0
'
Экстремум
3
•
•
•
•
•
По графику производной
В 8. Повторяем. Учимся. Закрепляем. Тренируемся.
f’(x) = 0
точки пересечения
графика y=f’(x) с ОХ
Сколько ?
решение
•
16
Отрезок [9;16]
График y=f’(x)
ниже оси ОХ
f’(x)
≤ 0
функция y=f(x)
убывает
Х = 9
9
решение
4
9
•
График y=f’(x)
выше оси ОХ
4
Функция возрастает
большему Х
большее У;
f’(x)
≥ 0
решение
продолжение
8

ο
4. Найдите количество точек минимума функции f(x) на отрезке [0;20].
2
•
•
Монотонность у = f(x)
f(x) – с убывания на возрастание
5. Найдите промежутки убывания
функции f(x). В ответе укажите
сумму целых точек, входящих в эти
промежутки.
156
f’(x) ≤ 0
Промежутки, где у = f(x) - убывает
•
•
•
•
2
20
6. Найдите количество точек, в которых
касательная к графику функции f(x)
параллельна прямой y = 2x + 17 или
совпадает с ней.
6
f’(x) - угловой коэффициент касательной.
У параллельных прямых - К
f’(x) = 2
•
•
•
•
•
•
В 8. Повторяем. Учимся. Закрепляем. Тренируемся.
9
ο
21
По графику производной
На рисунке изображен график производной функции f(x), определенной на интервале (-1;21).
0
Отрезок [0;20]
Сколько ?
f’(x) - меняет знак с «-» на «+» !
решение
y = f’(x), №№ 4 - 6
График f’(x)
ниже оси ОХ
4
8
16
•
19
20
решение
2
+3
+4
+8
+9
+10
+11
+12
+13
+14
+15
+16
+19
+20
f’(x) =
- К равны !!!
2
•
Прямая у = f’(x) = 2
решение

А можно и так!
На рисунке изображён график функции y = f(x) и
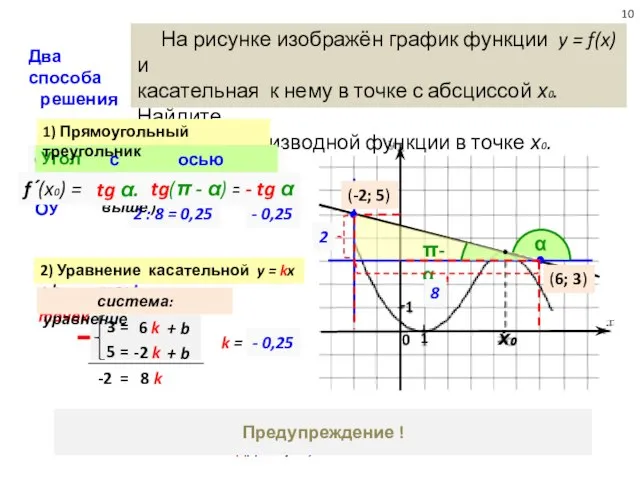
касательная к нему в точке с абсциссой х₀. Найдите
значение производной функции в точке х₀.
х₀
•
ı
ı
1
1
0
Прямые,
параллельные:
оси ОХ
оси ОУ
•
Угол
α
•
π- α
•
2
8
2 : 8 = 0,25
- 0,25
(точка уровнем ниже),
(точка уровнем выше ).
наклона касательной
к положительному
направлению
с
осью ОХ
f΄(x₀) =
tg α.
tg(π - α) =
- tg α
2) Уравнение касательной y = kx + b
1) Прямоугольный треугольник
Координаты точек
(6; 3)
(-2; 5)
подставить в уравнение
система:
3 =
6 k
+ b
5 =
-2 k
+ b
-2 =
8 k
k =
- 0,25
10
Два способа
решения
Предупреждение!
Если на касательной точки не выделены,
сделайте это сами – пересечение линий клеток
на касательной (вдруг встретится такое задание).
Предупреждение !

На рисунке изображены график функции у= f(x)
и касательная к этому графику, проведённая в
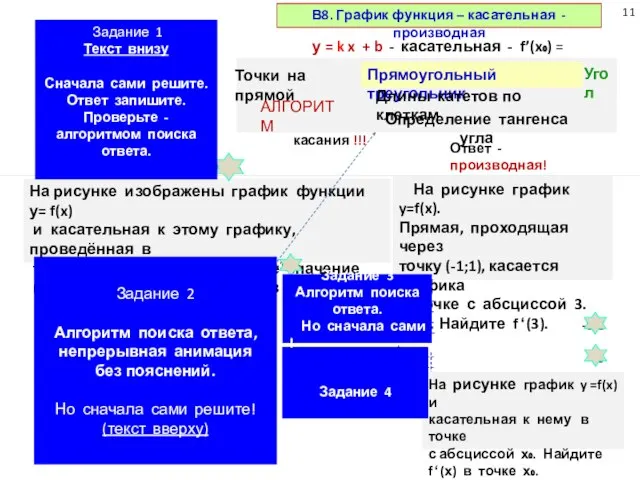
точке с абсциссой х₀. Найдите значение
производной функции у=f(x) в точке х₀.
у = k x + b
- касательная - f’(x₀) = k
k - угловой коэффициент - тангенс угла наклона прямой
к положительному → оси ОХ !!!
Производная функции в точке касания !!!
Ответ - производная!
В8. График функция – касательная - производная
•
•
= - tg α
tg (π – α)
α
•
•
Y=f(x)
На рисунке график y=f(x).
Прямая, проходящая через
точку (-1;1), касается графика
в точке с абсциссой 3.
Найдите f ̒ (3).
На рисунке график y =f(x) и
касательная к нему в точке
с абсциссой х₀. Найдите
f ̒ (х) в точке х₀.
Y=f(x)
х₀
•
•
11
0,25
-1,25
-0,5
- 1
Задание 4
α
Задание 3
Алгоритм поиска ответа.
Но сначала сами !
π - α
Точки на прямой
Прямоугольный треугольник
Угол
Длины катетов по клеткам
Определение тангенса угла
АЛГОРИТМ
Задание 1
Текст внизу
Сначала сами решите.
Ответ запишите.
Проверьте -
алгоритмом поиска ответа.
Задание 2
Алгоритм поиска ответа,
непрерывная анимация
без пояснений.
Но сначала сами решите!
(текст вверху)

•
•
•
•
•
•
o
o
Производная, функция, касательная - понятийный аппарат
В 8 и В 11
*График функции и её свойства - выход на производную и касательную
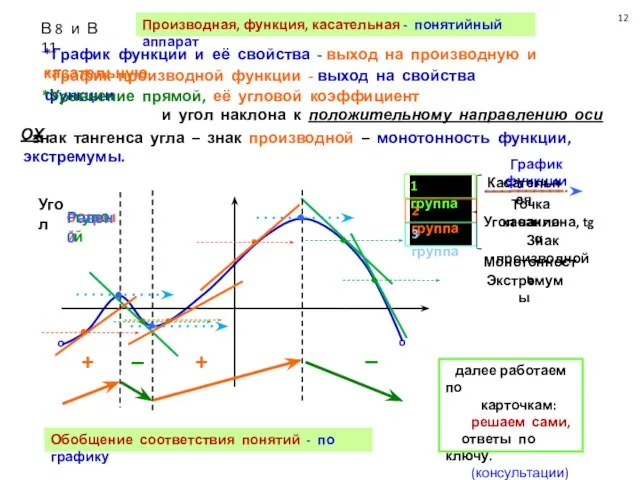
*График производной функции - выход на свойства функции
*Уравнение прямой, её угловой коэффициент
и угол наклона к положительному направлению оси ОХ -
График функции
Касательная
Угол наклона, tg α
Знак производной
Монотонность
Экстремумы
далее работаем по
карточкам:
решаем сами,
ответы по ключу.
(консультации)
•
•
•
Точка касания
12
1 группа
2 группа
3 группа
Обобщение соответствия понятий - по графику
- знак тангенса угла – знак производной – монотонность функции, экстремумы.
Угол
острый
тупой
Равен 0
+
+
–
–

+
Промежутки
+
–
+
возрастает
+
+
монотонности
–
–
–
убывает
функция
°
°
знак
y = f’(x)
э
к
с
т
р
е
м
у
м
y = f(x)
•
•
•
•
•
•
•
•
///////////////////
///////////////////
//////////////////////////////
///////
///////
/////////////
/////////////
/////////////////////////
f(x) > 0
f(x) < 0
°
°
Возможный график y = f’(x)
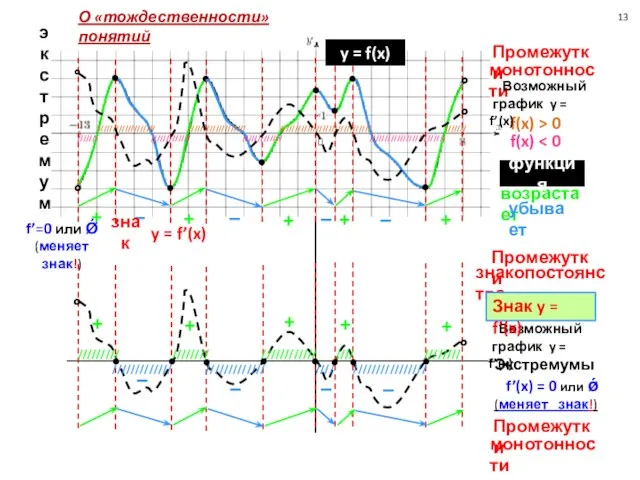
Возможный
график y = f’(x)
Промежутки
знакопостоянства
///////// //////// //////////// //// ////////
///////////// ///////////// //// ////////////////
•
•
•
•
•
•
•
•
Экстремумы
f’(x) = 0 или ǿ
(меняет знак!)
13
Знак y = f’(x)
+
+
–
+
+
+
–
–
–
О «тождественности» понятий
Промежутки
монотонности
°
°
f’=0 или Ǿ
(меняет знак!)