Содержание
- 2. Содержание Основные понятия Демонстрация сечений Метод следов Метод вспомогательных сечений Комбинированный метод
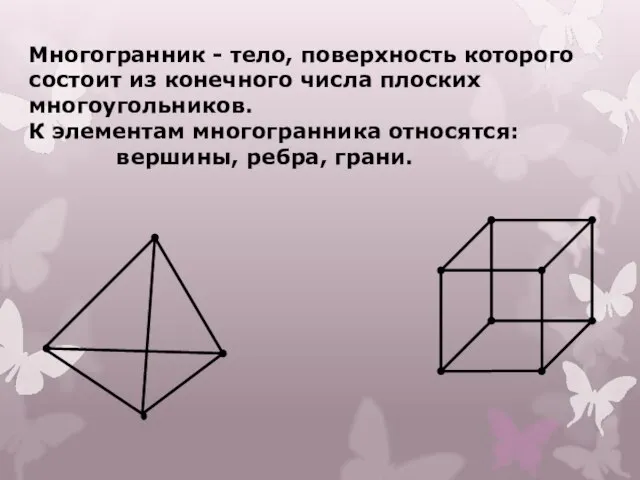
- 3. Многогранник - тело, поверхность которого состоит из конечного числа плоских многоугольников. К элементам многогранника относятся: вершины,
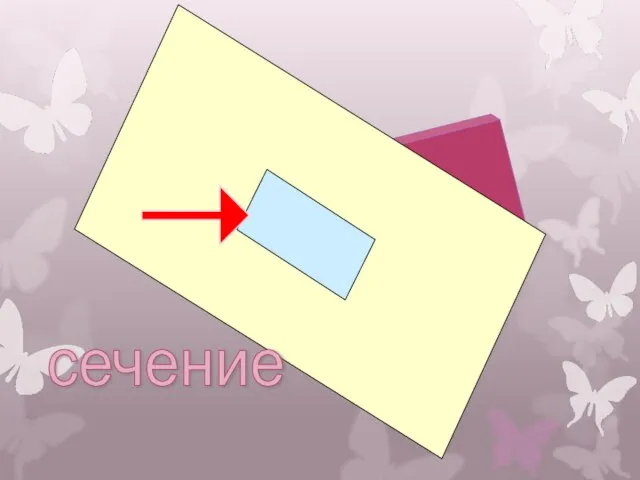
- 4. Сечением поверхности геометрических тел называется Плоская фигура, полученная в результате пересечения тела плоскостью и содержащая точки,
- 5. сечение
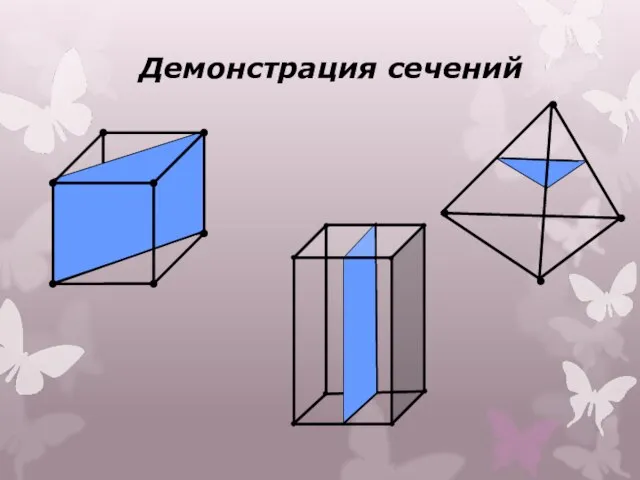
- 6. Демонстрация сечений
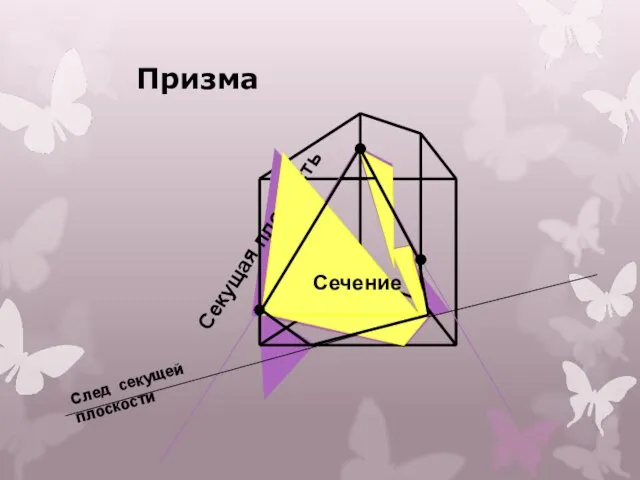
- 7. Призма Секущая плоскость Сечение
- 8. Секущая плоскость пересекает грани многогранника по прямым, а точнее по отрезкам - разрезам. Так как секущая
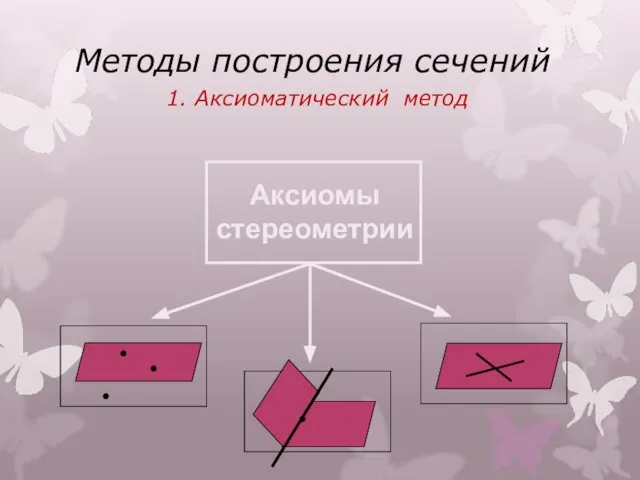
- 9. Методы построения сечений 1. Аксиоматический метод Аксиомы стереометрии
- 10. Аксиоматический метод Метод следов Суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей
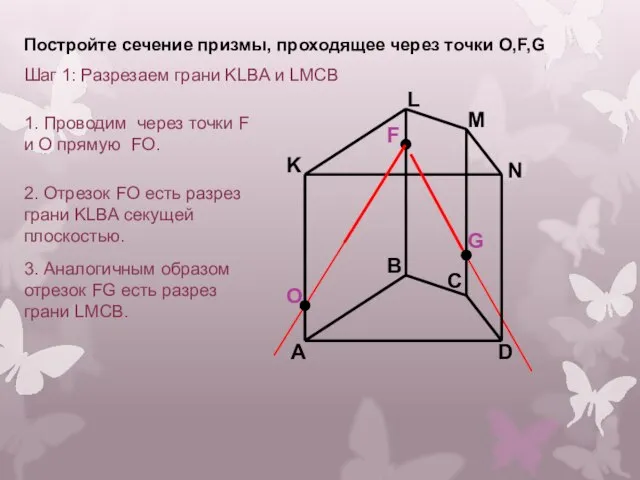
- 11. A B C D K L M N F G 1. Проводим через точки F и
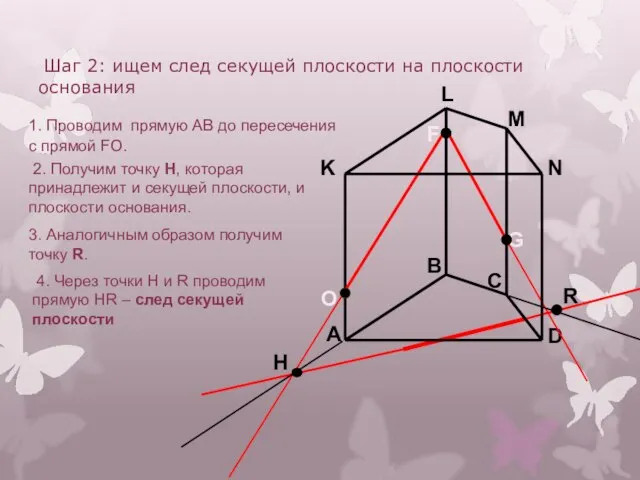
- 12. A B C D K L M N F G Шаг 2: ищем след секущей плоскости
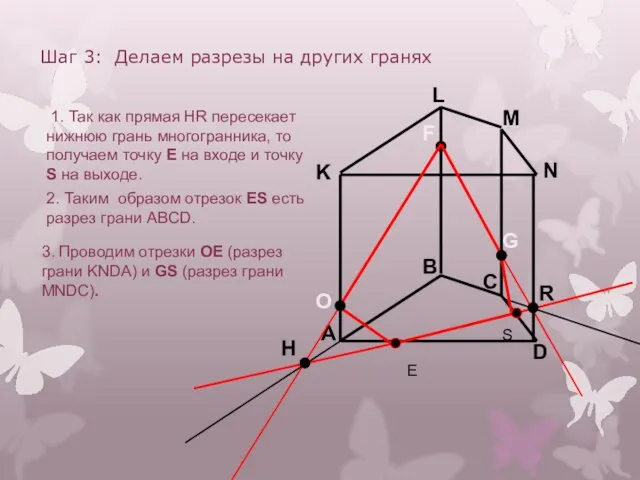
- 13. A B C D K L M N F G Шаг 3: Делаем разрезы на других
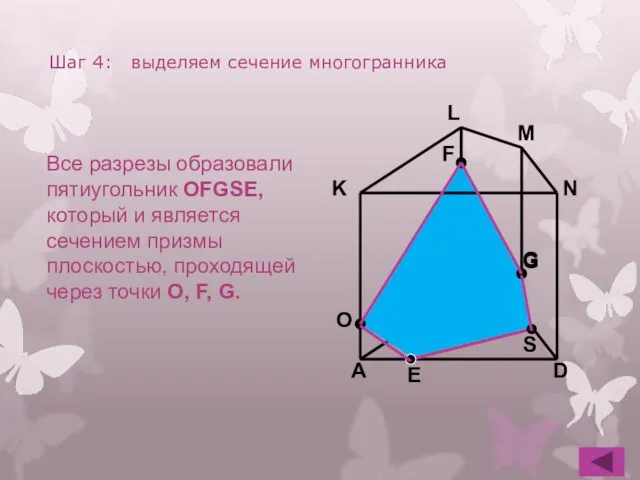
- 14. C B A D K L M N F G Шаг 4: выделяем сечение многогранника Все
- 15. Метод вспомогательных сечений Этот метод построения сечений многогранников является в достаточной мере универсальным. В тех случаях,
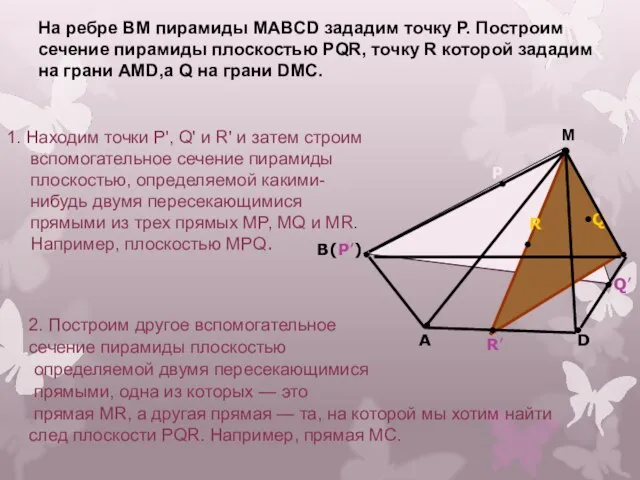
- 16. На ребре BM пирамиды MABCD зададим точку Р. Построим сечение пирамиды плоскостью PQR, точку R которой
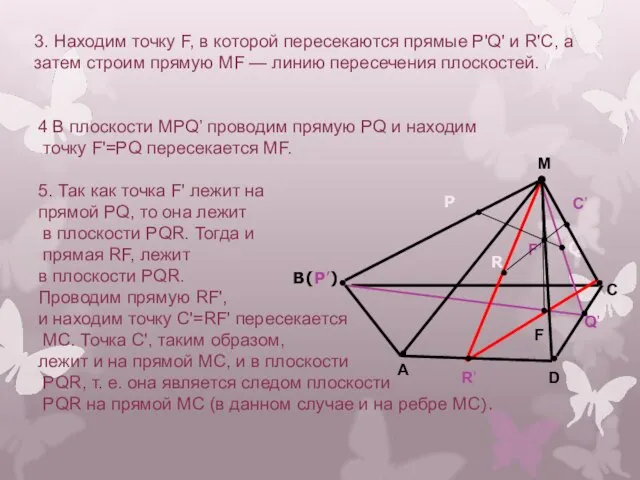
- 17. 3. Находим точку F, в которой пересекаются прямые Р'Q' и R'С, а затем строим прямую MF
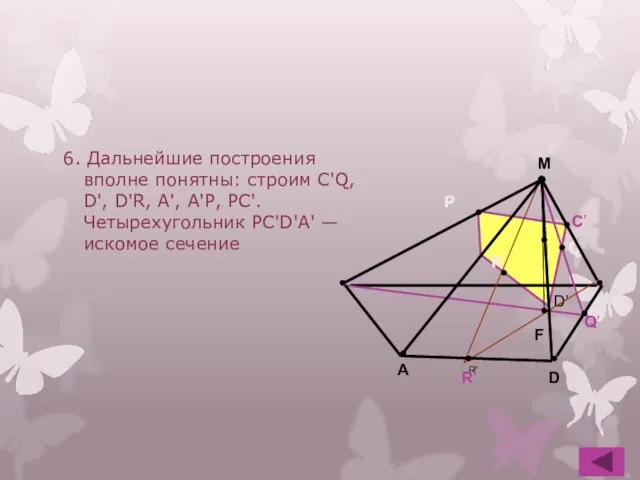
- 18. 6. Дальнейшие построения вполне понятны: строим C'Q, D', D'R, А', А'Р, РС'. Четырехугольник РС'D'А' — искомое
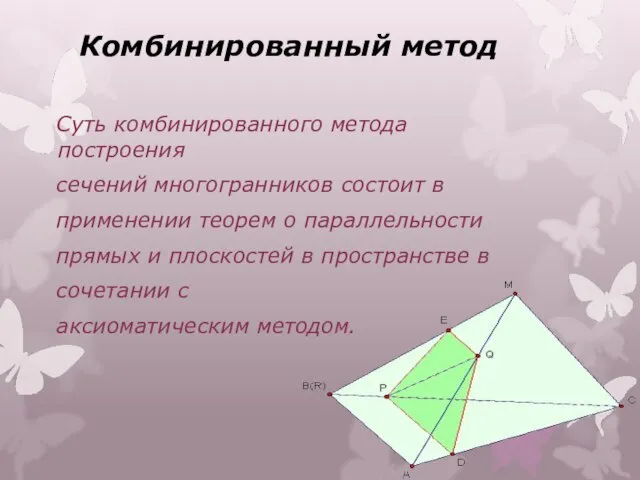
- 19. Комбинированный метод Суть комбинированного метода построения сечений многогранников состоит в применении теорем о параллельности прямых и
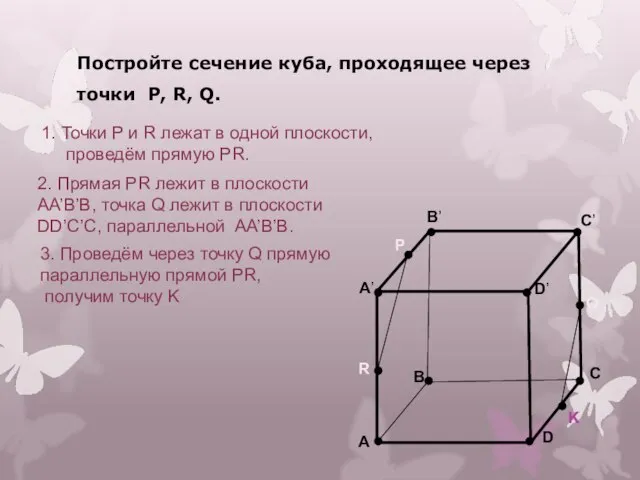
- 20. Постройте сечение куба, проходящее через точки P, R, Q. A B C D A’ B’ C’
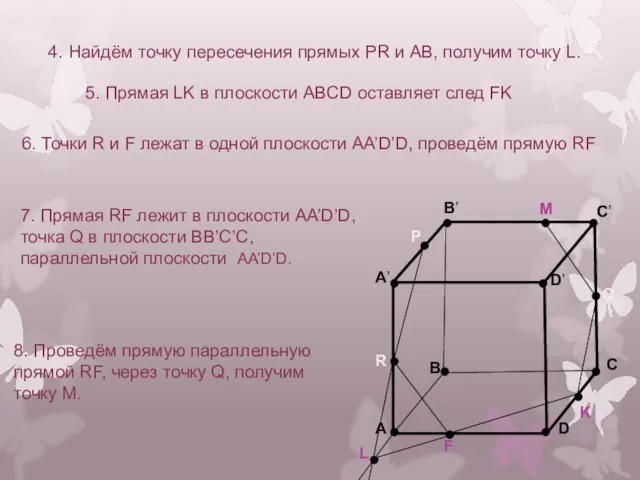
- 21. A B C D A’ B’ C’ D’ R P Q 4. Найдём точку пересечения прямых
- 23. Скачать презентацию





 Услуга «Персональный ассистент»
Услуга «Персональный ассистент» Возможные дефекты облицовывания, их предупреждение и устранение
Возможные дефекты облицовывания, их предупреждение и устранение Основы проектной деятельности
Основы проектной деятельности Беспилотная доставка
Беспилотная доставка Картинг, от макета к реальности
Картинг, от макета к реальности Подготовка учащихся к олимпиадам по обществознанию праву, ЕГЭ и ОГЭ
Подготовка учащихся к олимпиадам по обществознанию праву, ЕГЭ и ОГЭ Уважаемые партнеры! Мы рады представить эксклюзивную новинку Color Symphony винил вспененный на флизелине1,06*10m
Уважаемые партнеры! Мы рады представить эксклюзивную новинку Color Symphony винил вспененный на флизелине1,06*10m Очищение и кондиционирование. Предложение для клиента
Очищение и кондиционирование. Предложение для клиента Разработка блок-схем в программе Microsoft Office Visio 2007
Разработка блок-схем в программе Microsoft Office Visio 2007 Вероятность прогноза температур рельсов
Вероятность прогноза температур рельсов Приемная кампания 2012
Приемная кампания 2012 Запрос и предложение - способ коммуникации между заказчиком и исследовательским агентством
Запрос и предложение - способ коммуникации между заказчиком и исследовательским агентством Развитие речи. Заметка. Герои Алтайской земли.
Развитие речи. Заметка. Герои Алтайской земли. Презентация на тему Формирование универсальных учебных действий в образовательном пространстве начальной школы в условиях внедр
Презентация на тему Формирование универсальных учебных действий в образовательном пространстве начальной школы в условиях внедр Презентация по информатике на тему: Поколение третье. Интегральные схемы.
Презентация по информатике на тему: Поколение третье. Интегральные схемы. Цех по изготовлению металлоконструкций п. Балезино. Бизнес-план
Цех по изготовлению металлоконструкций п. Балезино. Бизнес-план Презентация
Презентация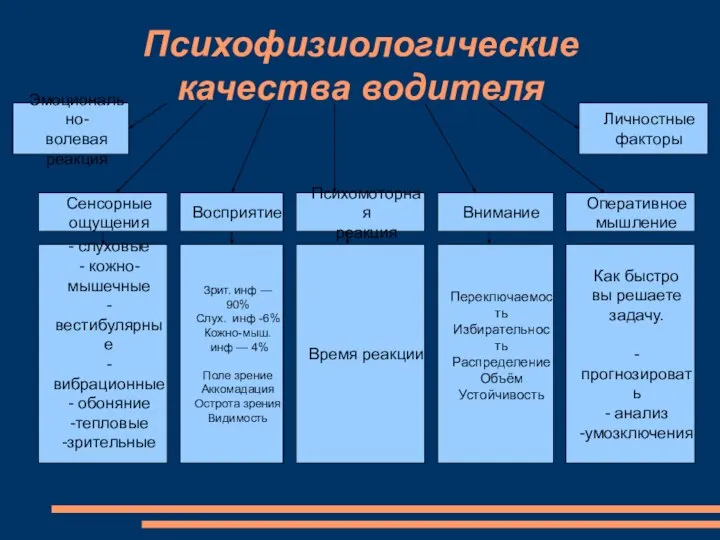 Эмоционально-волевая реакция. Психофизиологические качества водителя
Эмоционально-волевая реакция. Психофизиологические качества водителя Создание изображения для фона презентации
Создание изображения для фона презентации Восстановление славянских государств
Восстановление славянских государств Масла индустриальные ГОСТ 17479.4-87
Масла индустриальные ГОСТ 17479.4-87 Симметрия в живой и неживой природе Выполнили: студенты 1-го курса Факультет: Таможенное дело Группа: Т-116с. Уваров Антон, Панкрат
Симметрия в живой и неживой природе Выполнили: студенты 1-го курса Факультет: Таможенное дело Группа: Т-116с. Уваров Антон, Панкрат МОУ Медведская ООШ ФГОС начальная школа
МОУ Медведская ООШ ФГОС начальная школа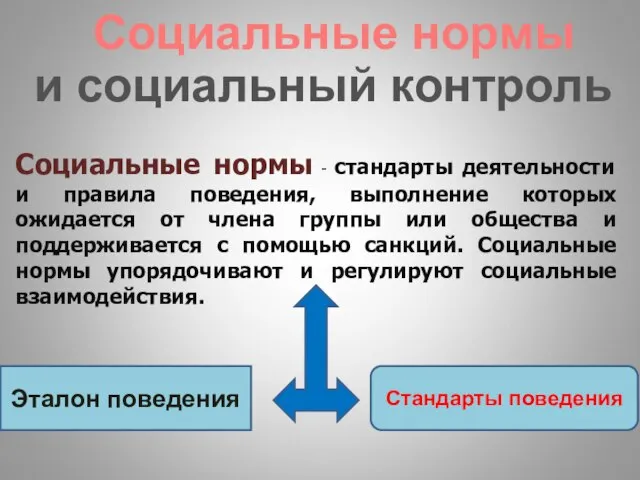 Социальные нормы и социальный контроль
Социальные нормы и социальный контроль .
. Презентация
Презентация Самая большая ошибка человека
Самая большая ошибка человека Neizvedannye_zemli
Neizvedannye_zemli