Сфера

1.Сфера и шар
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.
Данная точка О- центр сферы.
Данное расстояние R- радиус сферы.
Отрезок, соединяющий любые две точки сферы и проходящий через центр, называется диаметром сферы.
Тело, ограниченное сферой, называется шаром.
Центр, радиус и диаметр сферы называются центром, радиусом и диаметром шара

№1
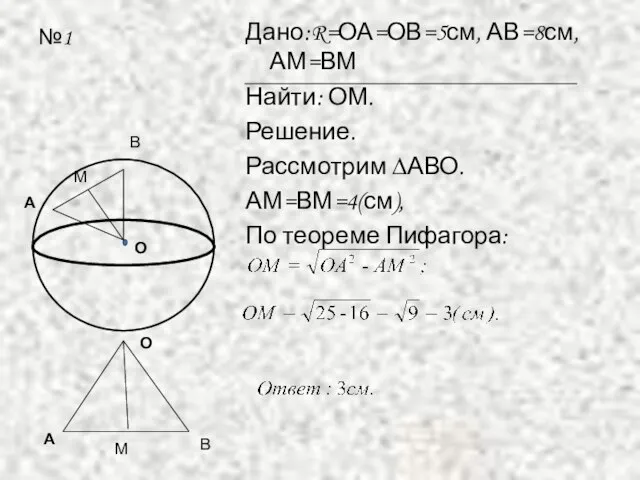
Дано:R=ОА=ОВ=5см, АВ=8см,АМ=ВМ
Найти: ОМ.
Решение.
Рассмотрим ∆АВО.
АМ=ВМ=4(см),
По теореме Пифагора:
В
М
В
М

2.Уравнение сферы
Охуz- заданная прямоугольная
система координат,
С(х0;у0;z0)-центр сферы,
М(х;у;z)- произвольная точка сферы.
СМ²=(х-х₀)²+(у-у₀)²+(z-z₀)²,
(х-х₀)²+(у-у₀)²+(z-z₀)²=R²-
уравнение сферы радиуса R
с центром С(х0;у0;z0).
М

№2.
Дано:
С(2;-1;5)-центр,
R=3.
Составьте
уравнение
сферы
Решение.
(х-х₀)²+(у-у₀)²+(z-z₀)²=R²- уравнение сферы радиуса R с центром С(х0;у0;z0).
(х-2)²+(у+1)²+(z-5)²=3²,
(х-2)²+(у+1)²+(z-5)²=9.
Ответ:(х-2)²+(у+1)²+(z-5)²=9.

№3.
Дано:
С(2;-1;5)-центр,
А(1;5;-1)-точка сферы.
Составьте
уравнение
сферы
Решение.
(х-х₀)²+(у-у₀)²+(z-z₀)²=R²- уравнение сферы радиуса R с центром С(х0;у0;z0).
(х-2)²+(у+1)²+(z-5)²=R²,
R²=(1-2)²+(5+1)²+(-1-5)²=1+36+36=73,
(х-2)²+(у+1)²+(z-5)²=73.
Ответ:(х-2)²+(у+1)²+(z-5)²=73.

№4 Найдите координаты центра сферы и её радиус.
х²+у²+z²=16,
(0;0;0)- центр сферы, R=4.
(х-3)²+(у-6)²+(z+7)²=121,
(3;6;-7)-центр сферы, R=11.
(х+2)²+у²+(z-1)²=36,
(-2;0;1)-центр сферы, R=6.