Содержание
- 2. План урока Повторяем изученный материал Роль геометрии, в частности вычисления объёмов геометрических тел, в древности и
- 3. Запишите названия представленных геометрических тел Проверь себя
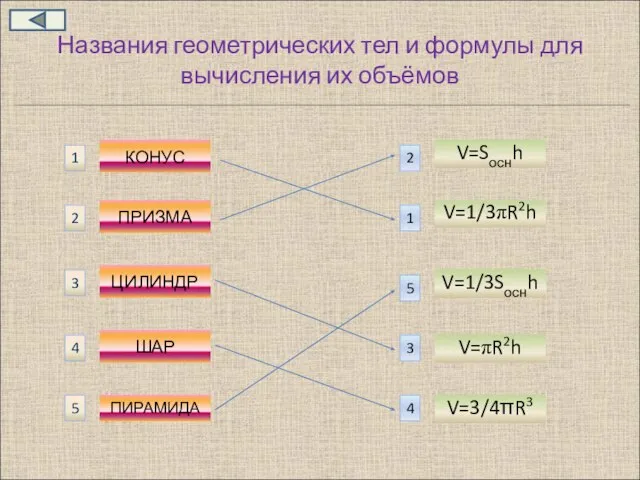
- 4. Сопоставьте названия геометрических тел и формулы для вычисления их объёмов КОНУС ПРИЗМА ЦИЛИНДР ПИРАМИДА ШАР V=Sоснh
- 5. Заполните пропуски Равные тела имеют … объёмы. Если тело составлено из нескольких тел, то его объём
- 6. Практическая геометрия у древних народов Практическое применение геометрии начинается с древних времён. Египтяне использовали эту науку
- 7. Геометрия и современность Велика роль геометрии и в нашем современном мире. В своей практической деятельности человек
- 8. Задача № 1 Сколько тюков сена вместится в сеновал, который имеет форму прямоугольного параллелепипеда и размеры
- 9. Задача № 2 Сколько тонн нефти может перевезти поезд, имеющий в своём составе 15 цистерн, если
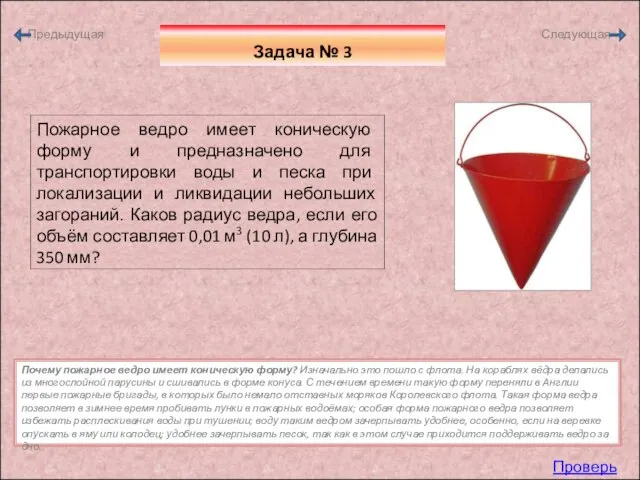
- 10. Задача № 3 Пожарное ведро имеет коническую форму и предназначено для транспортировки воды и песка при
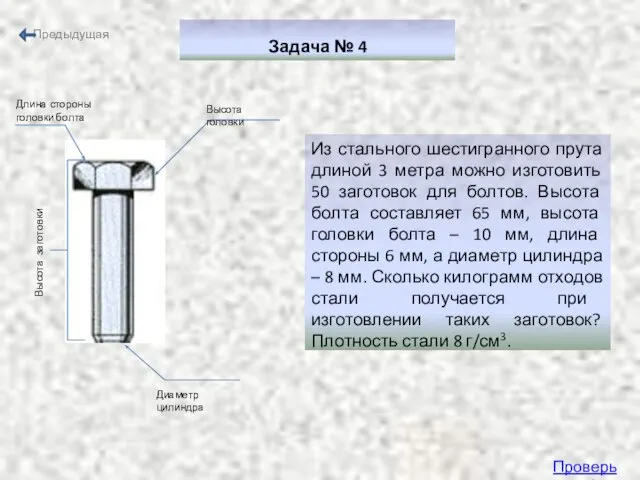
- 11. Задача № 4 Из стального шестигранного прута длиной 3 метра можно изготовить 50 заготовок для болтов.
- 12. Домашнее задание Повторить формулы для вычисления объёмов изученных геометрических тел. Придумать и решить задачу практического содержания
- 13. Спасибо за урок !
- 14. Названия представленных геометрических тел Цилиндр Призма Параллелепипед Пирамида Шар Конус
- 15. Названия геометрических тел и формулы для вычисления их объёмов КОНУС ПРИЗМА ЦИЛИНДР ПИРАМИДА ШАР V=Sоснh V=1/3πR2h
- 16. Заполните пропуски Равные тела имеют равные объёмы. Если тело составлено из нескольких тел, то его объём
- 18. Скачать презентацию












 Окрас и характер кошки
Окрас и характер кошки Буква К
Буква К 101100.62 Направление подготовки «Гостиничное дело»
101100.62 Направление подготовки «Гостиничное дело» Посадка под школу биохакинга
Посадка под школу биохакинга Год тигра
Год тигра Системы менеджмента качества на транспорте
Системы менеджмента качества на транспорте Ozon Premium Giftpacks. Подарочные гифтпаки для премиум-клиентов
Ozon Premium Giftpacks. Подарочные гифтпаки для премиум-клиентов Летняя практика в Восточно-Крымском историко-культурном музее-заповеднике
Летняя практика в Восточно-Крымском историко-культурном музее-заповеднике Лекция 3. Управление организационно-техническими системами. Управление проектами
Лекция 3. Управление организационно-техническими системами. Управление проектами ребования к проектно-сметной документации в рамках кредитного продукта Ипотечный кредит с льготной процентной ставкой
ребования к проектно-сметной документации в рамках кредитного продукта Ипотечный кредит с льготной процентной ставкой ОСТЕОПОРОЗ
ОСТЕОПОРОЗ Учебный тренажёр ЕГЭ - Орфография и пунктуация
Учебный тренажёр ЕГЭ - Орфография и пунктуация Геополитическое и экономико-географическое положение России (ЭГП)
Геополитическое и экономико-географическое положение России (ЭГП) Презентация на тему Рельеф России
Презентация на тему Рельеф России Юридическая компания Whitebridge Consult трудовое право
Юридическая компания Whitebridge Consult трудовое право STM-1/4 STM-4/16
STM-1/4 STM-4/16 30 лет кафедре «Теплогазоснабжение и вентиляция, процессы и аппараты химической технологии» (ТГВ ПАХТ)
30 лет кафедре «Теплогазоснабжение и вентиляция, процессы и аппараты химической технологии» (ТГВ ПАХТ) Рекламное агентство
Рекламное агентство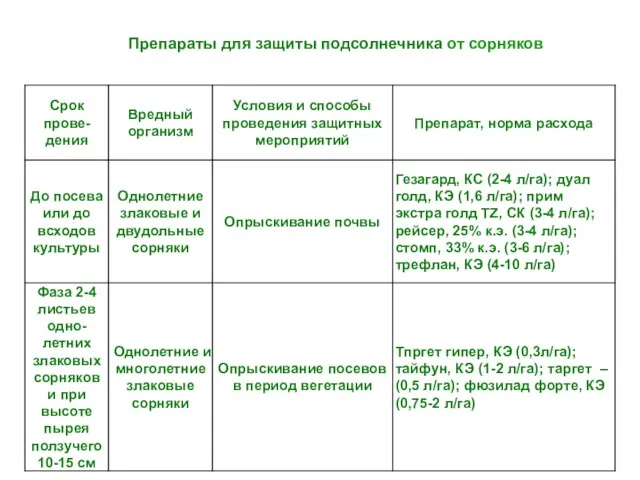 Препараты для защиты подсолнечника от сорняков
Препараты для защиты подсолнечника от сорняков Олимпийские игры
Олимпийские игры Времена года
Времена года Презентация на тему Биосферный заповедник Брянский лес
Презентация на тему Биосферный заповедник Брянский лес  Строение цветка 6 класс
Строение цветка 6 класс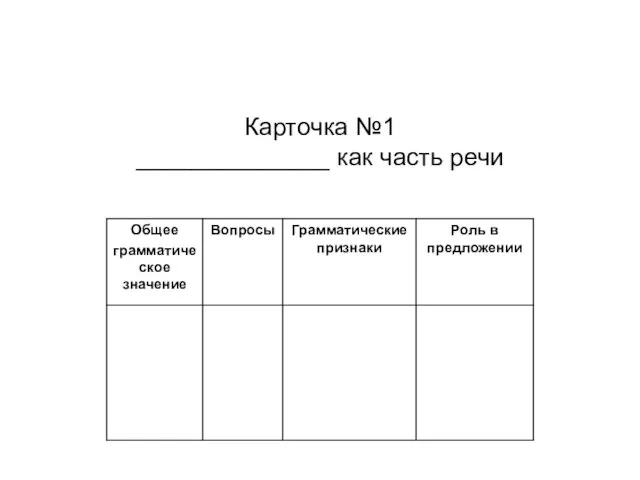 Карточка №1______________ как часть речи
Карточка №1______________ как часть речи 1
1 Разделочная доска с росписью по городецким мотивам
Разделочная доска с росписью по городецким мотивам Приливные электростанции
Приливные электростанции Презентация на тему Государственное регулирование оплаты труда
Презентация на тему Государственное регулирование оплаты труда