Сферические координаты

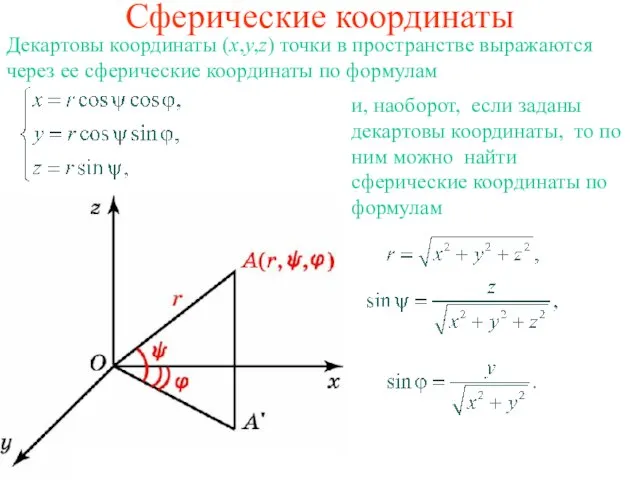
Сферические координаты
Декартовы координаты (x,y,z) точки в пространстве выражаются через ее сферические координаты по формулам
и, наоборот, если заданы декартовы координаты, то по ним можно найти сферические координаты по формулам

Сферические координаты
Точки на сфере, имеющие одинаковый угол ψ, образуют окружность, которая называется параллелью. Точки, имеющие одинаковый угол φ, образуют полуокружность, называемую меридианом.
Дуга большой окружности, соединяющая две точки сферы, является кратчайшим путем на сфере между этими двумя точками. Такой путь называют ортодромией, что в переводе с греческого означает "прямой бег".
Кривая, образующая равные углы с разными меридианами, называется локсодромия, что в переводе с греческого означает "косой бег".

Упражнение 1
Найдите декартовы координаты следующих точек пространства, заданных своими сферическими координатами: (1,45°,120°), (2,-30°,-90°), (1,90°, 60°).

Упражнение 2
Найдите сферические координаты следующих точек пространства, заданных своими декартовыми координатами: A(1,1,1), B(-1,0,1), C(0,0,2).

Упражнение 3
Найдите сферические координаты вершин куба, задаваемого в декартовых координатах системой неравенств

Упражнение 4
Точка A имеет сферические координаты (r, ψ, ϕ). Найдите сферические координаты точки, симметричной данной, относительно: а) координатных плоскостей; б) осей координат; в) начала координат.
Ответ: а) (r, -ψ, ϕ), (r, ψ, 180о-ϕ), (r, ψ, -ϕ);
б) (r, -ψ, -ϕ), (r, -ψ, 180о-ϕ), (r, ψ, 180о+ϕ);
в) (r, -ψ, 180о+ϕ).

Упражнение 5
Найдите геометрическое место точек пространства, сферические координаты которых удовлетворяют условиям: а) r постоянно; б) ψ постоянно; в) ϕ постоянно.
Ответ: а) Сфера;
б) коническая поверхность;
в) полуплоскость.

Упражнение 6
Какая фигура в пространстве задается неравенствами: а) 0 ≤ r ≤ 1, 0 ≤ ψ; б) 0 ≤ r ≤ 1, 0 ≤ ϕ ≤ π; в) 0 ≤ r ≤ 1, 0 ≤ ψ, 0 ≤ ϕ ≤ π?
Ответ: а) Полушар;
б) полушар;
в) четверть шара.

Упражнение 7
Найдите расстояние между точками, заданными своими сферическими координатами: A( ,0°,45°), B(2,60°,0°).
Ответ: 2.

Упражнение 8
Где закончится локсодромия, образующая острый угол с меридианами, при ее продолжении в обе стороны?
Ответ: На полюсах.

Упражнение 9
Напишите уравнение сферы в сферических координатах
Ответ: r = 1.