Шар . Сечение шара.

Устно:
1) Дайте определение окружности.
2)Круга
3)Определение касательной к окружности.
4)формулы длины окружности и площади круга.
02.12.2011

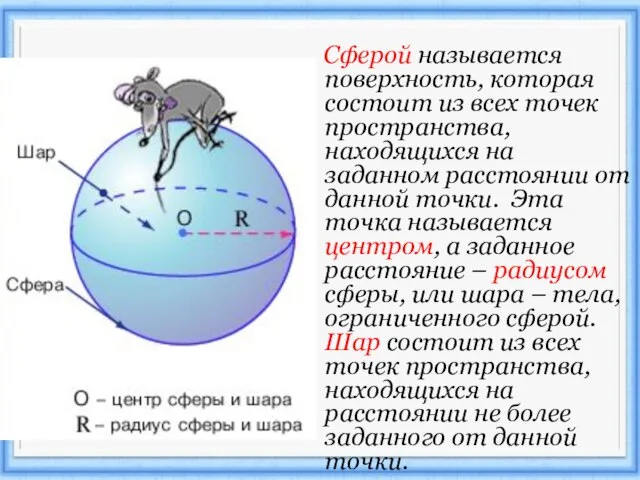
Сферой называется поверхность, которая состоит из всех точек пространства, находящихся на заданном расстоянии от данной точки. Эта точка называется центром, а заданное расстояние – радиусом сферы, или шара – тела, ограниченного сферой. Шар состоит из всех точек пространства, находящихся на расстоянии не более заданного от данной точки.

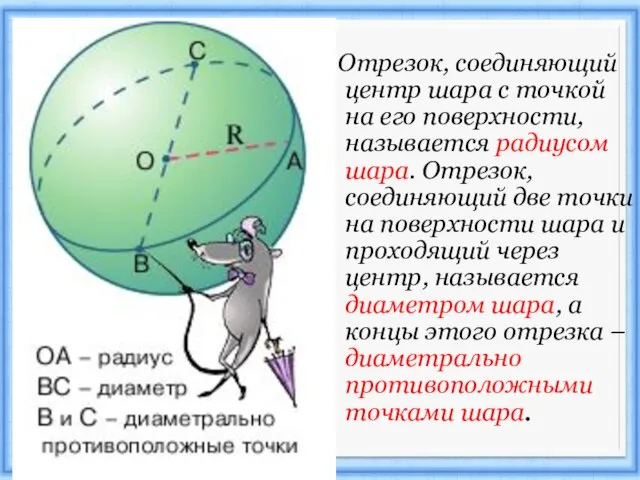
Отрезок, соединяющий центр шара с точкой на его поверхности, называется радиусом шара. Отрезок, соединяющий две точки на поверхности шара и проходящий через центр, называется диаметром шара, а концы этого отрезка – диаметрально противоположными точками шара.

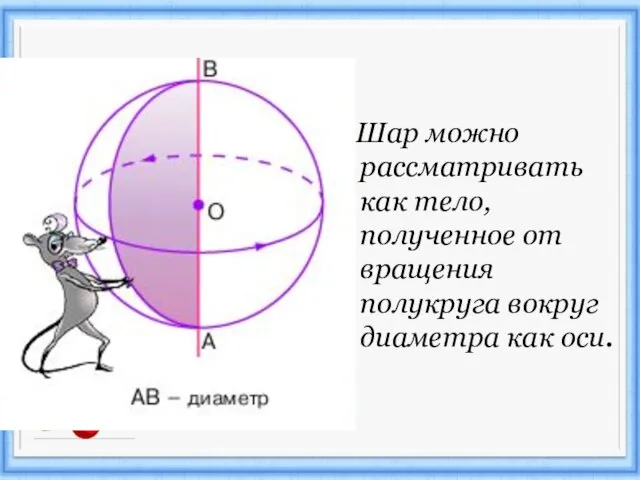
Шар можно рассматривать как тело, полученное от вращения полукруга вокруг диаметра как оси.

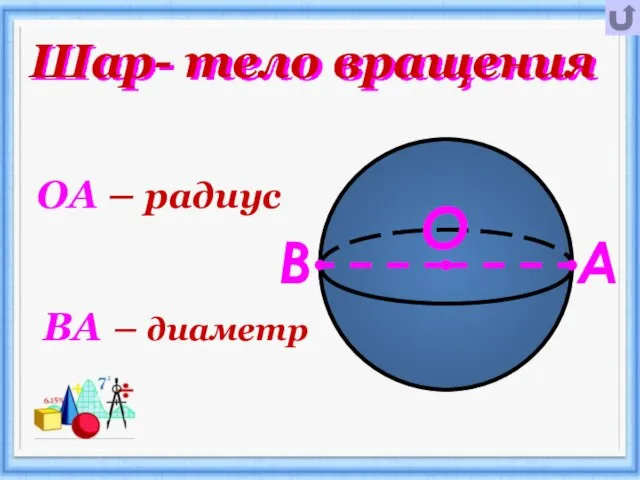
Шар- тело вращения
ОА – радиус
ВА – диаметр

Сечение шара плоскостью.
Любое сечение шара плоскостью есть круг. Центр этого круга – основание перпендикуляра, опущенного из центра шара на секущую плоскость.
Сечение, проходящее через центр шара, - большой круг. (диаметральное сечение).

Чем меньше расстояние от центра шара до плоскости, тем больше радиус сечения

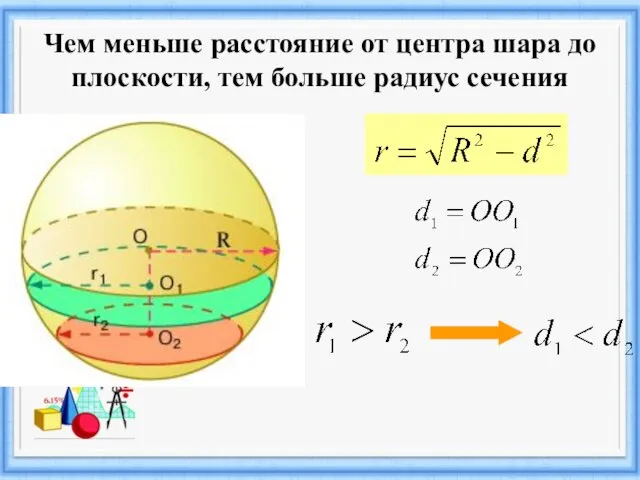
Наибольший радиус сечения получается, когда плоскость проходит через центр шара. Круг, получаемый в этом случае, называется большим кругом. Большой круг делит шар на два полушара.

Плоскость и прямая, касательные к сфере
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью. Касательная плоскость перпендикулярна радиусу, проведенному в точку касания.

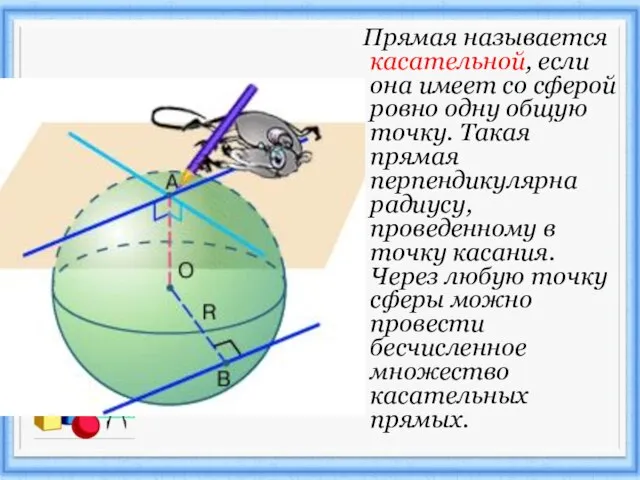
Прямая называется касательной, если она имеет со сферой ровно одну общую точку. Такая прямая перпендикулярна радиусу, проведенному в точку касания. Через любую точку сферы можно провести бесчисленное множество касательных прямых.

Решение задач
Учебник стр.95
№29
№31
№34