Слайд 2 Симметрия – это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны

от середины центра.
Симметрия определяется как совокупность свойств: порядка, однородности, соразмерности, гармоничности.
В современном понимании симметрия — это общенаучная философская категория, характеризующая структуру организации систем. Важнейшим свойством симметрии является сохранение (инвариантность) тех или иных признаков (геометрических, физических, биологических и т. д.) по отношению к вполне определенным преобразованиям.
Слайд 4 Ось, вокруг которой происходит поворот, называется осью симметрии. Это название не

случайное, так как в теории симметрии различают еще и сложные оси различного рода. Число совмещений фигуры с самой собой при одном полном обороте вокруг оси называется порядком оси.
Слайд 6 Под отражениями понимают любые зеркальные отражения — в точке, линии, плоскости.

Воображаемая плоскость, которая делит фигуры на две зеркальные половины, называется зеркальной симметрией.
Слайд 8
Поворотная симметрия выражающуюся в том, что органы располагаются в лучистых

направлениях вокруг одной главной продольной оси. От числа повторяющихся органов зависит порядок поворотной симметрии. Так, если вокруг продольной оси располагается 4 одинаковых органа, то поворотная симметрия в этом случае называется четырехлучевой. Если таких органов шесть, то и порядок симметрии будет шестилучевым, и т.д. Так как количество таких органов ограничено (часто 2,4,8 или кратное от 6), то и плоскостей симметрии можно провести всегда несколько, соответствующее количеству этих органов. Плоскости делят тело животного на одинаковые участки с повторяющимися органами. Поворотная симметрия характерна для малоподвижных и прикрепленных форм (двух-, четырёх-, восьми – и шести -лучевые кораллы, гидра, медузы, морские звезды).
Слайд 10 Винтовая симметрия есть симметрия относительно комбинации двух преобразований - поворота и

переноса вдоль оси поворота, т.е. идёт перемещение вдоль оси винта и вокруг оси винта. Она характерна тем, что при повороте на определённый угол часть тела немного проступает вперед и её размеры каждый следующий логарифмически увеличивает на определённую величину. Таким образом, происходит совмещение актов вращения и поступательного движения. Встречаются левые и правые винты.
Винтовая симметрия не бывает идеальной она или сужается или расширяется на конце.










 Алгоритмическое моделирование
Алгоритмическое моделирование Военная техника Великой Отечественной войны
Военная техника Великой Отечественной войны Дети войны
Дети войны Оценочные процедуры в РСОКО. Анализ опыта Чувашской Республики.
Оценочные процедуры в РСОКО. Анализ опыта Чувашской Республики. Самостоятельная работа № 3-4 от 06
Самостоятельная работа № 3-4 от 06 швы
швы Проект «Курить – жизнь загубить!»
Проект «Курить – жизнь загубить!» Воспитательный аспект образовательного процесса
Воспитательный аспект образовательного процесса Презентация на тему Металлы и неметаллы
Презентация на тему Металлы и неметаллы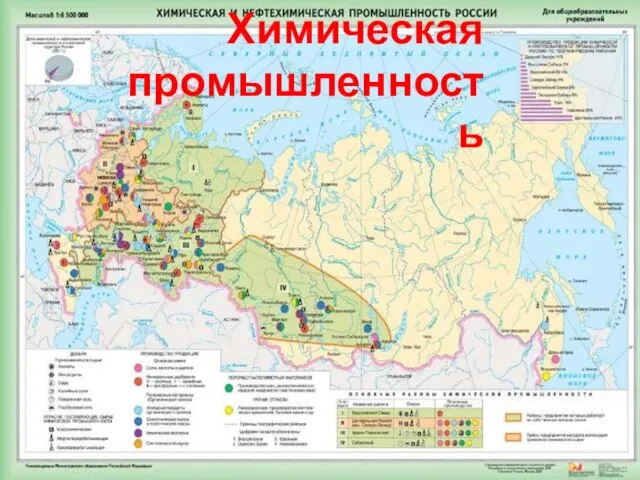 Презентация на тему Химическая промышленность
Презентация на тему Химическая промышленность  Презентация на тему Кто работает ночью 1 класс
Презентация на тему Кто работает ночью 1 класс учитель английского языка МОУ Прогимназия №1 Шашкова Лилия Владимировна г. Электрогорск Ул. Советская д. 5 кв. 72. Тел. 3-47-49 2008 год
учитель английского языка МОУ Прогимназия №1 Шашкова Лилия Владимировна г. Электрогорск Ул. Советская д. 5 кв. 72. Тел. 3-47-49 2008 год ИНФОРМАЦИОННАЯ СТРАТЕГИЯ ПО ВИЧ/СПИДу В РЕСПУБЛИКЕ БЕЛАРУСЬ
ИНФОРМАЦИОННАЯ СТРАТЕГИЯ ПО ВИЧ/СПИДу В РЕСПУБЛИКЕ БЕЛАРУСЬ Многообразие насекомых, их роль в природе и жизни человека
Многообразие насекомых, их роль в природе и жизни человека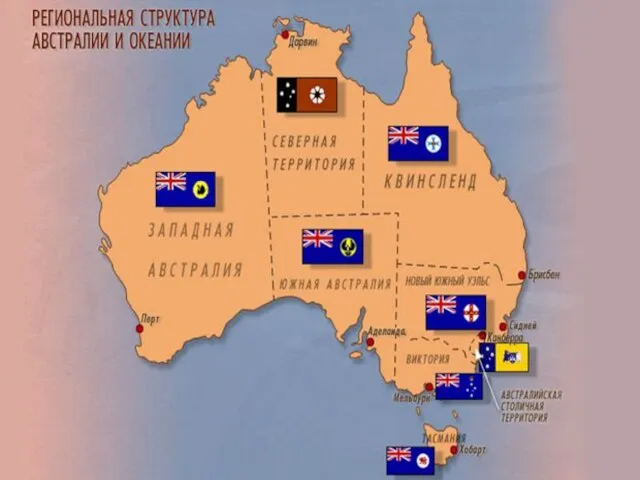 Австралия и Океания.
Австралия и Океания. Виды предложений по цели высказывания и по интонации
Виды предложений по цели высказывания и по интонации Моторные расстройства при паркинсонизме и их влияние на качество жизни пациента
Моторные расстройства при паркинсонизме и их влияние на качество жизни пациента Нектар воспевания святого имени – Намамрита
Нектар воспевания святого имени – Намамрита Зачетная работа. Организационная структура отеля Крокус
Зачетная работа. Организационная структура отеля Крокус Учение Платона о государстве и праве
Учение Платона о государстве и праве Политическая сфера общества
Политическая сфера общества Времена года. Зимний лес
Времена года. Зимний лес «Снимать можно чем угодно,
«Снимать можно чем угодно, Swot-анализ
Swot-анализ К 50- летию космонавтики. Звёздное небо -это небольшая часть безграничного космоса. Земляне всех поколений всегда смотрели на него с
К 50- летию космонавтики. Звёздное небо -это небольшая часть безграничного космоса. Земляне всех поколений всегда смотрели на него с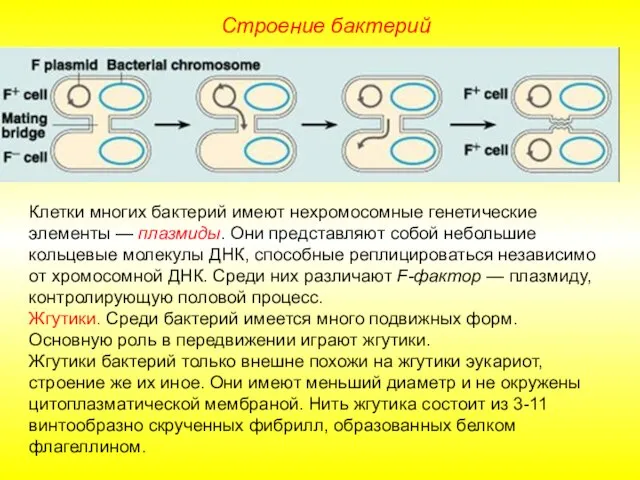 Строение бактерий
Строение бактерий Государство. понятие, признаки, сущность, социальное назначение, функции
Государство. понятие, признаки, сущность, социальное назначение, функции Шапки
Шапки