Синус, косинус и тангенс угла

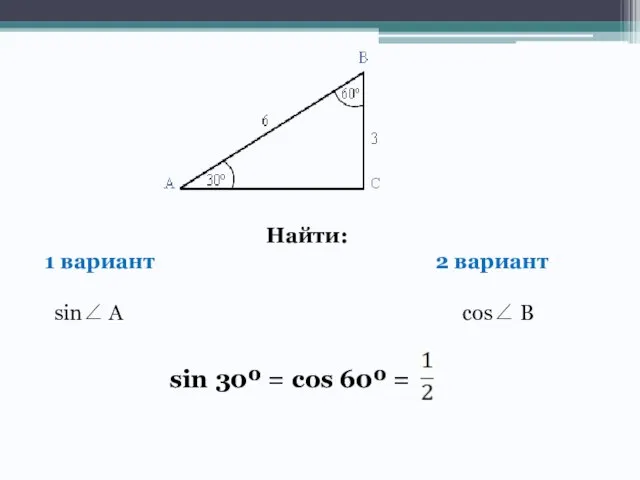
Найти:
1 вариант 2 вариант
sin A cos B
sin 30º = cos 60º =

Единичная полуокружность
Определение. Полуокружность называется единичной, если ее центр находится в начале координат, а радиус равен 1.

Синус, косинус,
тангенс угла
Синус угла – ордината у точки М
sin  = , MD = y, sin  = y.
Косинус угла – абсцисса х точки М
cos  = , OD = x, cos  = x.
Тангенс, катангенс угла
Т. к. tg = ,  tg = , ctg =
0 ≤  ≤ 180

Синус, косинус,
тангенс угла
Так как координаты (х; у) заключены в промежутках
0 ≤ у ≤ 1, - 1 ≤ х ≤ 1,
то для любого  из промежутка
0 ≤  ≤ 180
справедливы неравенства:
0 ≤ sin  ≤ 1,
- 1≤ cos  ≤ 1

Значения синуса и косинуса
для углов 0, 90 и 180
Так как точки А, С и B имеют координаты
А (1; 0), С (0; 1), В (-1; 0), то
sin 0 = 0,
sin 90 = 1,
sin 180 = 0,
cos 0 = 1,
cos 90 = 0,
cos 180 = - 1

Т.к. tg = , то при  = 90 тангенс угла  не определен.
tg 0  = 0, tg 180  = 0.
Т.к. ctg = , то при  = 0,  = 180  катангенс угла  не определен
ctg 90 = 0.
Значения тангенса и катангенса
0, 90 и 180

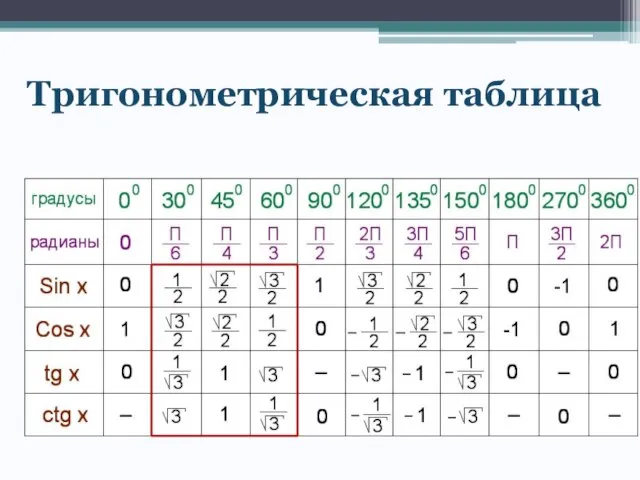
Тригонометрическая таблица

Основное тригонометрическое
тождество
Уравнение окружности
х2 + у2 = 1
sin = x, cos = y
0 ≤  ≤ 180
sin2  + cos2  = 1

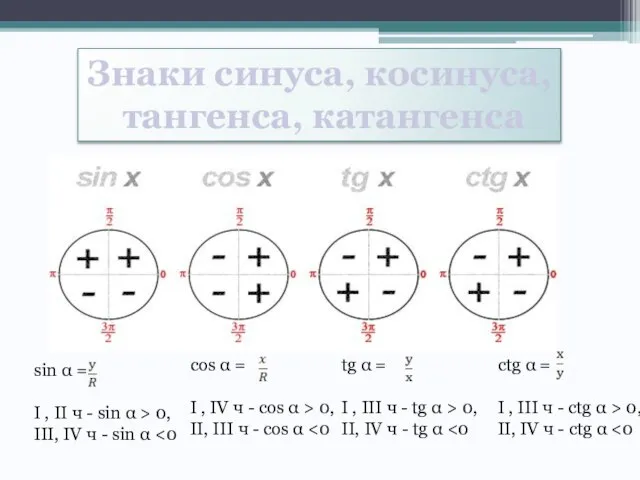
Знаки синуса, косинуса,
тангенса, катангенса
sin  =
I , II ч - sin  > 0, III, IV ч - sin  <0
cos  =
I , IV ч - cos  > 0, II, III ч - cos  <0
tg  =
I , III ч - tg  > 0, II, IV ч - tg  <0
ctg  =
I , III ч - ctg  > 0, II, IV ч - ctg  <0

Формулы приведения
sin (90 - ) = cos 
cos (90 - ) = sin  (5) при 0 ≤  ≤ 90,
sin (180 - )= sin 
cos (180 - ) = - cos  (6) при 0 ≤  ≤ 180

Формулы для вычисления
координат точки
М(сosα; sinα). А ( x;y) – произвольная точка
sin  = y, cos  = x
М(cos ; sin ), (cos ; sin ), (х;у)
По лемме о коллинеарных векторах
= ОА∙ , поэтому
x = ОА ∙ cos ,
y = OA ∙ sin .

Домашнее задание
§1, пп. 93 - 95, №№ 1014, 1015 (б, г)

Урок окончен
До свидания!