Синус, косинус и тангенс в прямоугольном треугольнике

В папирусе Ахилеса часто встречается прямоугольный треугольник, который занимает почетное место и в вавилонской геометрии. Землемеры и поныне прибегают к прямоугольному треугольнику для определения расстояний и т.п.
Фалес решил найти высоту одной из громадных пирамид. Он воткнул длинную палку вертикально в землю и сказал: «Когда тень от этой палки будет той же длины, что и сама палка, тень от пирамиды будет той же длины, что и высота пирамиды».

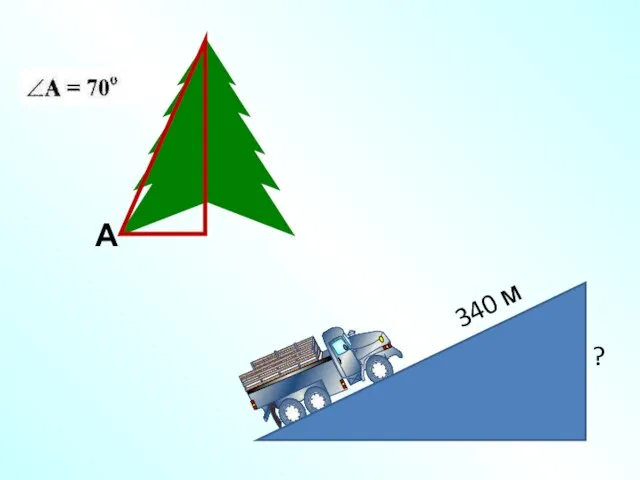
С самолета радируют на ледокол, что он находится над разыскиваемым объектом на высоте 1 км. С ледокола определяют угол повышения α=300 (углом повышения называется угол между лучом зрения, идущим к фиксированной точке, и горизонталью). Найдите расстояние от ледокола до разыскиваемого объекта.

Помогите лилипуту определить рост Гулливера

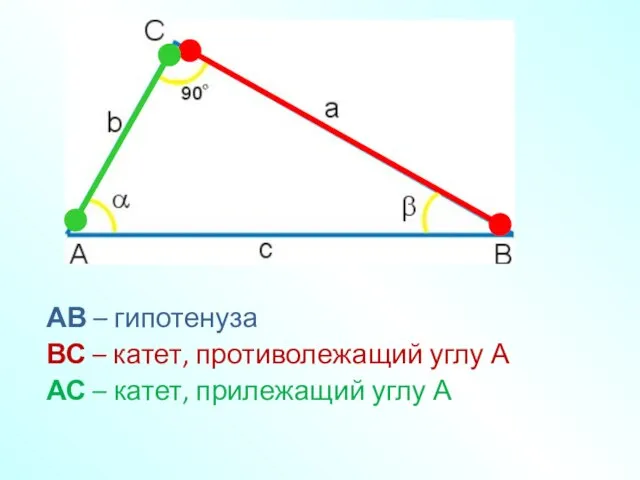
АВ – гипотенуза
ВС – катет, противолежащий углу А
АС – катет, прилежащий углу А

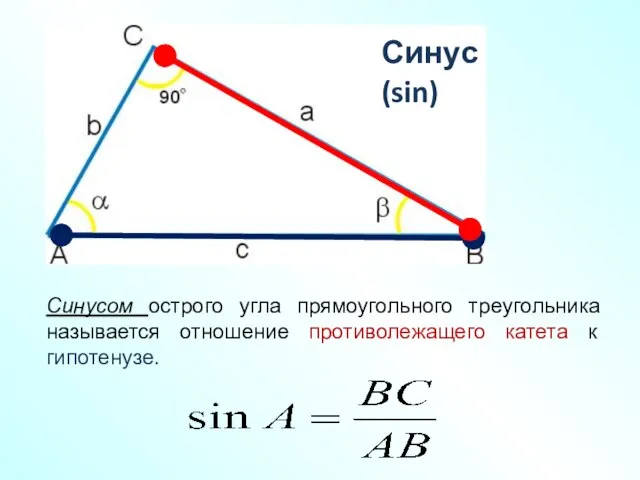
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Синус (sin)

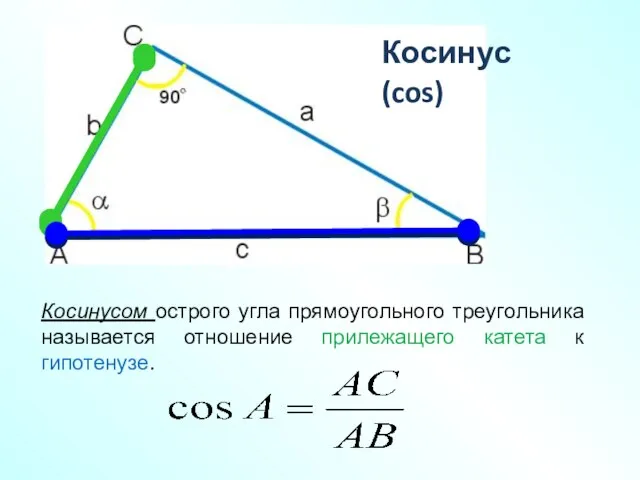
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Косинус (cos)

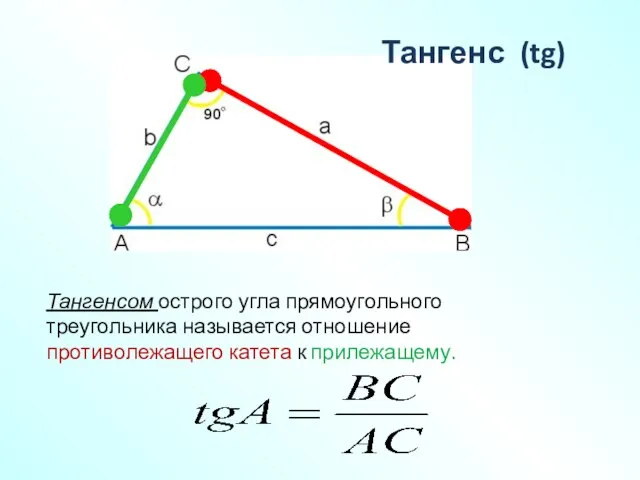
Тангенс (tg)
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Индийские математики синус обозначали словом "джива" (букв. - тетива лука). Арабы переделали этот термин в "джиба", который в дальнейшем превратился в "джайо" - обиходное слово арабского языка, означающее изгиб, пазуха, складка одежды, что соответствует латинскому слову sinus.
Тангенс (от лат. tangens - касающийся)
Из истории терминов

Задача
Найдите синус, косинус и тангенс острого угла А прямоугольного треугольника с катетами 8 см и 25 см.
А
С
В
25
8

ФИЗМИНУТКА

Чтобы сильным стать и ловким,
Приступаем к тренировке.
Носом вдох, а выдох ртом.
Дышим глубже, а потом
Шаг на месте, не спеша.
Как погода хороша!
Мы проверили осанку
И свели лопатки.
Мы походим на носках,
И идём на пятках.
ФИЗМИНУТКА НА УРОКЕ –
ЗДОРОВЬЕ НА ГОДЫ!

Тригонометрические тождества
Основное тригонометрическое тождество:
2) Тангенс угла равен отношению синуса к косинусу этого угла.

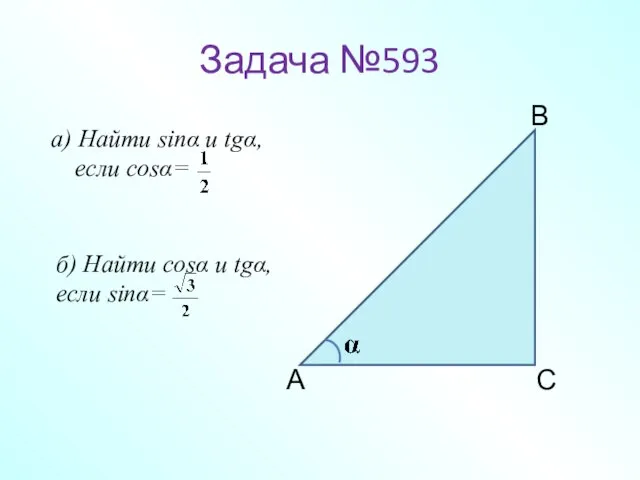
Задача №593
а) Найти sinα и tgα, если cosα=
А
В
С
б) Найти cosα и tgα,
если sinα=

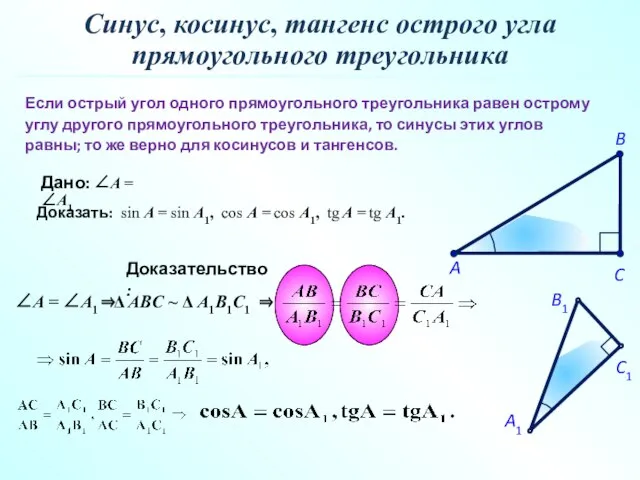
Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны; то же верно для косинусов и тангенсов.
Доказательство:
Синус, косинус, тангенс острого угла
прямоугольного треугольника
Дано: ∠A = ∠A1
∠A = ∠A1 ⇒
Δ ABC ~ Δ A1B1C1 ⇒
Доказать: sin A = sin A1, cos A = cos A1, tg A = tg A1.

Задание на дом:
п. 66, в. 15-17, № 591(в, г), 593(б, г), 592* (а, б) .