Системысчисления.

Числа не управляют миром, но показывают, как управляется мир.
Иоганн Гете

Веселая разминка
На столе стояло 3 стакана с вишней. Оксана съела один стакан вишен. Сколько стаканов осталось?
3 стакана

В клетке находятся три кролика. Три девочки попросили дать им по одному кролику. Просьба девочек была удовлетворена, каждой из них дали кролика. И все же в клетке остался один кролик. Как могло так случиться?
Одной девочке дали кролика в клетке
Веселая разминка

В классе, где шел урок, находилось 20 человек. Из них 10 девочек. Сколько в классе находилось мальчиков?
9 мальчиков, учительница, тоже девочка.
Веселая разминка

Определите четное число или нечетное:
а) 1012
б) 1102
в) 10012
г) 1002
Сформулируйте критерий четности в
двоичной системе.
Ответ: четное число в двоичной системе счисления оканчивается на 0, а нечетное – на 1.
а) 1012 = 510 ; б) 1102 = 610 ; в) 10012 = 910 ; г) 1002 = 410
Эврика!!!

Было 11 яблок. После того как каждое яблоко разрезали пополам, стало 110 половинок.
Возможно ли это?
Обоснуйте ответ.
Ответ:
Да, если считать числа в задаче представленными в двоичной системе счисления: 112=1⋅20 + 1⋅21=310;
1102 = 0⋅20 + 1⋅21 + 1⋅22 = 2 + 4 = 610

Некогда был пруд, в центре которого рос один лист водяной лилии. Каждый день число таких листьев удваивалось, и на десятый день вся поверхность пруда уже была заполнена листьями лилий. Сколько дней понадобилось, чтобы заполнить лилиями половину пруда? Сосчитать сколько листьев выросло к десятому дню?

Ответ: 9 дней, 512 листьев.

Сколько больших планет обращается вокруг солнца?
Подсказка: 1001
Сколько глаз у пиявки?
Подсказка: 1010
Сколько вершков в аршине?
Подсказка: 10000
Сапоги какого размера носил дядя Степа?
Подсказка: 101101
Сколько лет спала Спящая красавица из сказки Шарля Перро?
Подсказка: 1100100
9
100
45
16
10

=11001002
=1001012
Двоичная система счисления
0 и 1

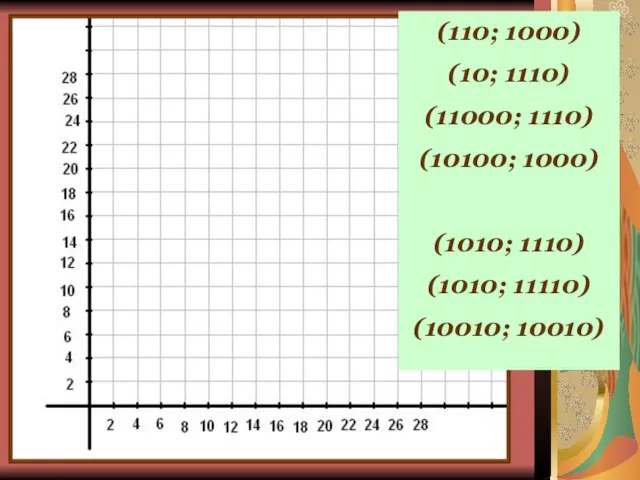
(110; 1000)
(10; 1110)
(11000; 1110)
(10100; 1000)
(1010; 1110)
(1010; 11110)
(10010; 10010)

При археологических раскопках в Китае и Индии были найдены квадратные амулеты. Квадрат разделен на девять квадратиков, в каждом из которых написано по одному числу от 1 до 9. Замечательно, что суммы чисел в каждой строке, в каждом столбце и каждой из двух диагоналей были равны одному и тому же числу 15. Такие квадраты стали называть магическими.

В древности магические квадраты очень уважали и приписывали им различные мистические свойства. Говорят, если надо было решиться на какое-то опасное дело, их с магическими целями рисовали на бумажке и съедали. Такое же кушанье предлагали в качестве панацеи от всех болезней. Бытовало поверье, что выгравированный на серебре магический квадрат защищает от чумы. Даже сегодня среди атрибутов европейских прорицателей можно увидеть магические квадраты.
А.Дюрера, гравюра «Меланхолия»
(1514)

Молодцы!

Единичная («палочная»)
Период палеолита.
10-11 тысяч лет до н.э.
2,5 тысяч лет до н.э.
Древнеегипетская
десятичная
- единицы
- десятки
- сотни
= 3 4 5
или

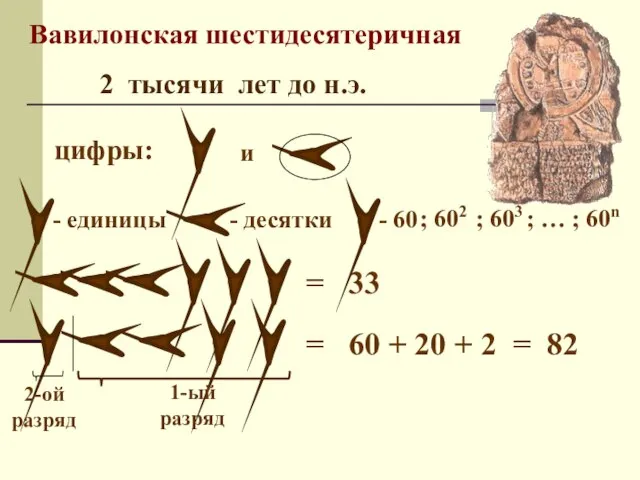
2 тысячи лет до н.э.
Вавилонская шестидесятеричная
- единицы
- десятки
= 33
цифры:
и
2-ой
разряд
1-ый
разряд
= 60 + 20 + 2 = 82

Алфавитные системы
Древняя Русь
1
2
3
4
5
6
7
8
9
10
«… В год 6367. Варяги из заморья
взимали дань…»
- тысячи
- тьма: х10 000
100 000 - легион
1000 000 - леодр
1050 - колода
(«Повесть временных лет»)
. . .
= 10 000
«более сего несть человеческому уму разумевати»
- титло
«Аз»
«Веди»
«Глаголь»
«Добро»
«Есть»
«Зело»
«Земля»
«Иже»
«Фита»
«И»

Пушкин...
17 30 48
140 10 01
126 138
140 3 501
Веселые:
2 15 42
42 15
37 08 5
20 20 20!
7 14 100 0
2 0 0 13
37 08 5
20 20 20!
Поэзия в числах
(Читать вслух и с выражением)