Лорана, поделив числитель на знаменатель.
b2z3 + b1z2
b2z3 – b2с2z2 – b2с1z – b2c0
–
+ [b2с1 + (b1 + b2с2)с2]z-2 + …
(b1 + b2с2)z2 + b2с1z + b2c0
(b1 + b2с2)z2 – (b1 + b2с2)с2z – (b1 + b2с2)c1 – (b1 + b2с2)c0z-1
–
Получим h[0] = b2; h[1] = b1 + b2c2 = b1 + b2(3 – b2).
1) Переходная характеристика начинается в момент подачи единичного скачка и h[0] = b2.
2) Значение h[1] может быть и больше, и меньше h[0] в зависимости от значений b1 и b2.
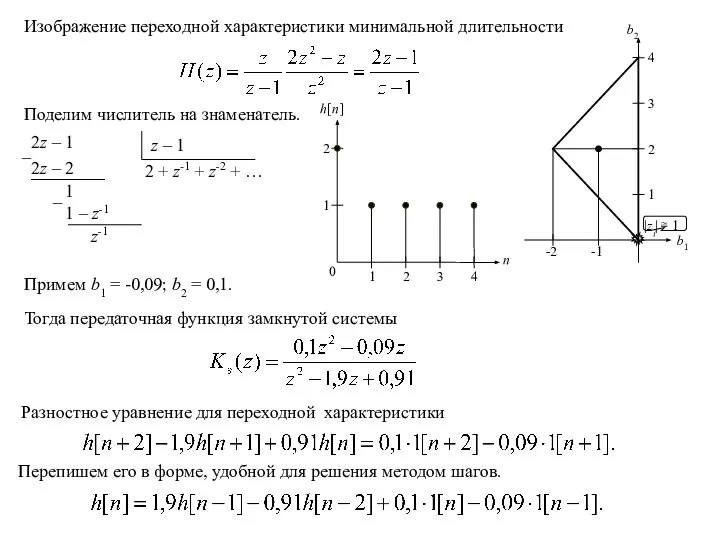
Найдем переходную характеристику минимальной длительности, которая будет при нулевых корнях характеристического уравнения z2 + (b2 – 2)z + (1 + b1) = 0, то есть при b2 – 2 = 0 и 1 + b1 = 0. Откуда следует b1 = –1 и b2 = 2.
b2
+ (b1 + b2c2)z-1


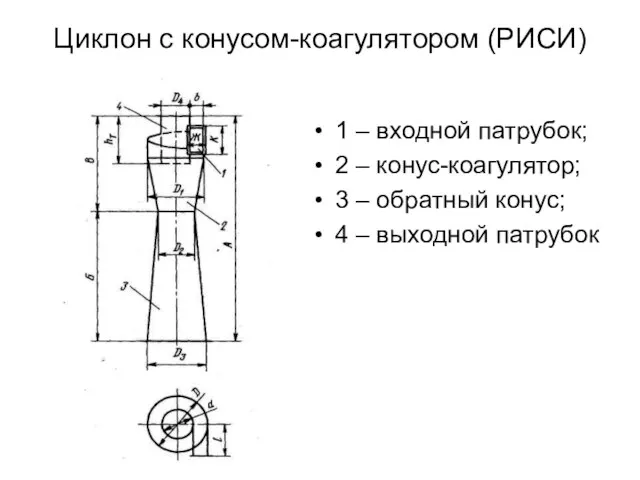 Циклон с конусом-коагулятором (РИСИ)
Циклон с конусом-коагулятором (РИСИ)  Маркетинговое исследование рынка молочной продукции по дисциплине маркетинг
Маркетинговое исследование рынка молочной продукции по дисциплине маркетинг Инновационные подходы к формированию индивидуальных программ реабилитации инвалидов.
Инновационные подходы к формированию индивидуальных программ реабилитации инвалидов. People’s Princess. The Truly Story About Lady Diana
People’s Princess. The Truly Story About Lady Diana Рисунки к 100 летию Г.А. Илизарова
Рисунки к 100 летию Г.А. Илизарова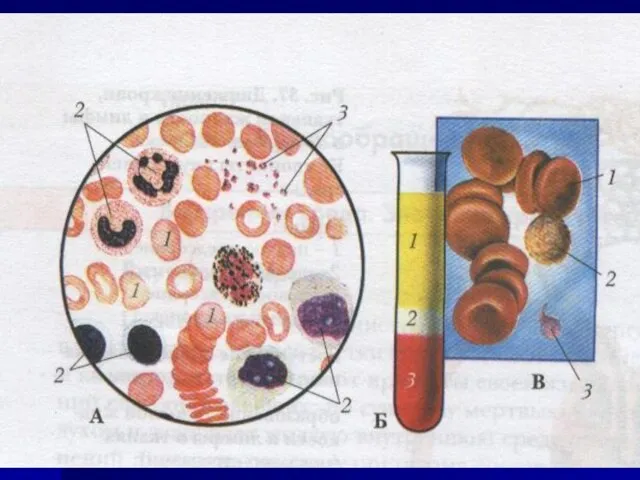 Строение сердца. Сердце – это жизнь
Строение сердца. Сердце – это жизнь Презентация на тему Характеристика биогеоценоза
Презентация на тему Характеристика биогеоценоза  Концептуальные и методологические аспекты управления финансами российских вузов
Концептуальные и методологические аспекты управления финансами российских вузов ACQUISITION OPPORTUNITIES IN RUSSIAN BRAKE
ACQUISITION OPPORTUNITIES IN RUSSIAN BRAKE  Проект БАРС. Требования к кандидатам
Проект БАРС. Требования к кандидатам Функции контроллера
Функции контроллера Памятник собакам
Памятник собакам General Pharmacology
General Pharmacology Личный кабинет педагога. Помощь в работе или дополнительная нагрузка
Личный кабинет педагога. Помощь в работе или дополнительная нагрузка Общая информация, логотип отеля
Общая информация, логотип отеля Ювенальная юстиция Австралии
Ювенальная юстиция Австралии Современный компьютер. Перспективы развития
Современный компьютер. Перспективы развития Русская школа генетики
Русская школа генетики Научная работа «Глушение скважин в условиях АНПД. Эффективность внедрения технологических растворов для ремонта скважин на осно
Научная работа «Глушение скважин в условиях АНПД. Эффективность внедрения технологических растворов для ремонта скважин на осно Поиск ключевого бизнес-партнёра. Система сопровождения и развития ключевых партнеров
Поиск ключевого бизнес-партнёра. Система сопровождения и развития ключевых партнеров Электрический ток
Электрический ток The Big Bang Social Theory!
The Big Bang Social Theory! Презентация на тему Гестозы
Презентация на тему Гестозы Afischa-1
Afischa-1 ОТКРЫТЫЙ ИНСТИТУТ ОХРАНЫ ТРУДА, ПРОМЫШЛЕННОЙБЕЗОПАСНОСТИ И ЭКОЛОГИИ
ОТКРЫТЫЙ ИНСТИТУТ ОХРАНЫ ТРУДА, ПРОМЫШЛЕННОЙБЕЗОПАСНОСТИ И ЭКОЛОГИИ 1.1. Каждый из 500 студентов посещают три спецкурса. Спецкурс только по математике, только по математике и физике, только по физике и а
1.1. Каждый из 500 студентов посещают три спецкурса. Спецкурс только по математике, только по математике и физике, только по физике и а Пермский государственный национальный исследовательский университетИтоги научно-исследовательской работы университета в 2011 го
Пермский государственный национальный исследовательский университетИтоги научно-исследовательской работы университета в 2011 го Война с Ганнибалом
Война с Ганнибалом